Problems and solutions

Résultat:

$650$

En 2012, le pommier mesurait $5\mathrm{dm}=50\mathrm{cm}$. Chacune des 10 années suivantes, il pousse de $600\mathrm{mm}=60\mathrm{cm}$. En 2022, la hauteur est donc $50\mathrm{cm}+10\cdot 60\mathrm{cm}=650\mathrm{cm}$.

Résultat:

$1600$

Il suffit de compter le nombres de côtés que Anne a parcouru. On peut facilement compter $20$ côtés, ce qui correspond à une distance totale de $20\cdot 80m=1600m$.

Résultat:

$16$

La vitesse moyenne de George est le résultat de la division de la distance totale qu’il a parcouru par le temps qu’il a mis pour parcourir cette distance. À partir du graphique, on peut déterminer que George a parcouru $16\mathrm{km}$ en $1h$. Sa vitesse moyenne sur cette course est donc de $16\mathrm{km}∕h$.

Résultat:

$5$

Tout d’abord, on doit passer par la lettre N. Si on prend le N qui est à deux carrés à droite de la position initiale du jeton, on doit ensuite continuer par la lettre Á en bas à droite du N. À partir de cette position, on ne peut plus passer par une lettre B en se déplaçant vers la droite ou et vers le bas. Pour la première lettre, on doit donc passer par le N en dessous de la position initiale du jeton.

Si on passe ensuite par la lettre Á qui est de trois cases à droite du N, on aura le même problème que dans le cas précédent et on ne pourra pas atteindre un B. On passera donc plutôt par le Á en dessous du N.

Si on passe ensuite par le B en bas à gauche pour la troisième lettre, on n’aura qu’une possibilité pour arriver à la case avec la lettre J. Comme on passe par la lettre O par ce chemin, on a une première façon de déplacer le jeton.

Si on passe par le B au milieu de la grille pour la troisième lettre, on aura de deux possibilités pour passer par la lettre O. Si on prend le O dans la ligne du bas, il n’y a qu’un façon pour arriver à la lettre J. Si on prend l’autre O, alors on a trois possibilités pour arriver au J.

Tous les déplacements possible sont sur la figure suivante :

Au total, Daniel a donc $5$ façons de déplacer le jeton.

Résultat:

$2$

Prenons les directions comme celles représentées sur la figure. Le rayon a été réfléchi du mur de droite après avoir parcouru un mètre de plus vers le haut. Cela signifie qu’il va toucher le mur de gauche deux mètres plus haut que la position de Marc. Ensuite, il sera réfléchi du mur de gauche de façon à ce qu’il touche le mur de droite en ayant parcouru un mètre de plus vers le haut. Il touchera donc le coin où il y a le ballon. On peut voir la trajectoire du ballon sur la figure suivante :

Le rayon sera donc réfléchi $2$ fois.

Résultat:

$6$

Laura peut faire $24$ kilomètres en 1 heure sur son vélo. Comme $3$ kilomètres font $1$ "versl’école", Laura peut parcourir $24:3=8$ versl’école en une heure. Mais un "périodedecours" n’est que $\frac{3}{4}$ d’une heure. Donc si Laura parcourt $8$ versl’école en une heure, elle parcourt $\frac{3}{4}\cdot 8=6$ versl’école en 3/4 d’heure (1 périodedecours). Laura peut donc aller à une vitesse de 6 versl’école par périodedecours sur son vélo.

Résultat:

$6$

Nous allons traiter tous les cas à partir du premier chiffre. Le seul nombre qui commence par le chiffre zéro est $0$. Mais 0 n’est pas un nombre strictement positif donc Alex ne le considère pas comme un nombre décroissant. Si le premier chiffre est $1$, alors il peut être suivi de $0$ ou de rien. Cela nous donne donc deux nombres décroissants $1$ et $10$. Si le premier chiffre est $2$, il peut être suivi de $1$, $0$ ou rien. Cela nous donne 4 solutions possible, $2$, $20$, $21$ et $210$. En tout, il y a donc $2+4=6$ nombres décroissants

Résultat:

$4$

Mathieu a couru $3\mathrm{km}$ à une vitesse de $9\mathrm{km}∕h$. Il a donc fini la course après $\frac{3\mathrm{km}}{9\mathrm{km}∕h}=\frac{1}{3}h=20\min$.

Marc roulait à une vitesse de $30\mathrm{km}∕h$, il a mis donc $\frac{3\mathrm{km}}{30\mathrm{km}∕h}=\frac{1}{10}h=6\min$ pour parcourir les 3 kilomètres de la course. Comme il a laissé une avance de $10$ min à Mathieu, il finit $6\min +10\min =16\min$ après son départ.

Marc a donc fini $20\min -16\min =4\min$ avant Mathieu.

Résultat:

$9$

Les numéros des places peuvent-elles inclure les chiffres $2$, $4$, $5$, $6$, $8$ ou $0$? Si c’était le cas, le numéro serait un multiple de $2$ ou $5$ ou le nombre obtenu après l’échange de ses chiffres sera un de ces multiples. Les nombres qu’on cherche ne pourront donc pas contenir ces chiffres, et seront donc composés dès chiffres $1$, $3$, $7$ et $9$. Seulement $16$ nombres satisfont cette condition :

De ces nombres, on peut éliminer les suivants : $33=3\cdot 11$, $39=3\cdot 13$, $77=7\cdot 11$, $91=7\cdot 13$, $93=3\cdot 31$ a $99=3\cdot 3\cdot 11$, car ils sont divisibles par d’autres nombres qu’eux et 1, donc ne sont pas des nombres premiers. On élimine également $19$ car quand on échange ses chiffres on obtient 91 qui n’est pas un nombre premier. Il nous reste les nombres suivants :

Mathieu a donc pu commander 9 tickets au maximum.

Résultat:

$2,5$

On peut calculer la distance qu’un enfant va parcourir en utilisant le théorème de Pythagore. Cette distance est de $\sqrt{{(3m)}^2+{(4m)}^2}=5m$. Comme dit dans l’énoncé, il faut $2s$ pour descendre le toboggan. L’enfant a donc une vitesse moyenne de $\frac{5m}{2s}=2,5m∕s$ quand il descend le toboggan.

Résultat:

$19$

Un rectangle peut être divisé en deux petits rectangles en utilisant un segment parallèle à l’un de ces deux côtés. Dans ce cas là, la longueur du segment est la même que celle du côté auquel il est parallèle.

Nous avons donc un rectangle avec un périmètre de $64m$, qui a un côté qui mesure $13m$. L’autre côté doit donc avoir une longueur $b$ telle que l’égalité suivante soit vraie : $2\cdot (13m+b)=64m$. On trouve que $b=32m-13m=19m$.

Comme dit au début du raisonnement, le côté $b$ doit avoir la même longueur que le chemin lorsqu’on utilise la seconde méthode pour diviser le rectangle en deux. Pour la seconde façon de construire le chemin, il aura une longueur de $19m$.

Résultat:

$587$

Nous allons appliquer le principe d’action-réaction. Il dit que si un objet $A$ agit sur un autre objet $B$ avec une certaine force $F$, alors l’objet $B$ agit également sur l’objet $A$ avec une force de même intensité mais dans la direction opposée. Dans notre problème, la terre attire Mathias avec une force gravitationnelle de $587N$. Mathias doit donc agir sur la terre avec une force gravitationnelle de même intensité, soit une force de $587N$.

Résultat:

$300$

Notons $s$ la distance que Sabine a parcouru. Si elle ne s’était pas arrêtée, couvrir cette distance lui aurait pris $\frac{s}{120\mathrm{km}∕h}$. Toutefois, comme elle a fait une pause de $30$ minutes, il lui a fallu $\frac{s}{120\mathrm{km}∕h}+0,5h$ pour couvrir la distance $s$. C’est à cause de cette pause que la vitesse moyenne de Sabine était seulement de $100\mathrm{km}∕h$. On obtient donc l’équation suivante :

Cela implique que Sabine a parcouru $300\mathrm{km}$.

Résultat:

$19$

L’estimation qui était à $10$ du nombre réel de problèmes résolus doit être la plus grande ou la plus petite des différentes estimations. Si c’était la plus petite, alors le nombre réel de problèmes résolus correctement doit être soit de $10-10=0$ ou $10+10=20$. La première option n’est pas possible dans ce cas, car les autres estimations seraient fausses de plus de $10$ problèmes. Pour la seconde option, les autres estimations diffèrent de $6$, $1$ et $9$, ce qui ne correspond pas aux différences données dans l’énoncé du problème. C’est donc le membre de l’équipe qui a fait l’estimation de $29$ problèmes résolus qui doit se tromper de $10$ problèmes. Pour une raison analogue au cas précédent, le nombre correct de problèmes résolus ne peut pas être $29+10=39$, et doit donc être $29-10=19$. Dans ce cas là, les différences par rapport aux estimations qui restent correspondent à celles données dans l’énoncé. L’équipe a donc résolu $19$ problèmes l’année dernière.

Résultat:

$24$

Commençons par réfléchir à ce qu’implique le fait que quelqu’un dise qu’une personne est (ou n’est pas) un espion. Par exemple, Alice dit que Daniel est un espion. Si Alice dit la vérité (donc si elle n’est pas un espion), alors Daniel est un espion. Si Alice ment (donc si elle est un espion), alors Daniel n’est pas un espion. Cela signifie que Alice et Daniel sont des opposés. Regardons maintenant la phrase de Bob. Si Bob dit la vérité (donc s’il n’est pas un espion), alors Cyril n’est également pas un espion. Mais si Bob ment (donc s’il est un espion), alors Cyril est aussi un espion. Donc on sait que soit ils sont tous les deux des espions, soit aucun des deux ne l’est. De la même façon, on peut déterminer que Daniel et Erik sont du même côté. Si Alice est un espion alors en plus d’elle, l’une des paires de Bob et Cyril ou Daniel et Erik devra contenir deux espions. Dans ce cas là, on aura au moins 3 espions, ce qui n’est un pas possible. Donc Alice ne peut pas être un espion. Comme elle dit que Daniel est un espion et qu’elle dit la vérité, alors Daniel est vraiment un espion. Le deuxième espion sera alors Erik car on a vu plus haut qu’il est du même côté que Daniel. Les deux qui restent, Bob et Cyril, ne seront donc pas des espions.

Les espions sont Daniel et Erik et la somme des nombres qui leur sont attribués est $8+16=24$.

Résultat:

$20$

Notons $x$ la taille du fichier. Si Mathieu charge le fichier sans compression, cela va prendre $\frac{x}{1\mathrm{MB}∕s}$. S’il décide de d’abord compresser le fichier, la compression va durer $\frac{x}{4\mathrm{MB}∕s}$. À ce moment-là, la taille du fichier sera $\frac{x}{2}$. Après $5$ secondes, Mathieu commence le chargement du fichier sur le drive et ce chargement va prendre $\frac{x}{2\cdot 1\mathrm{MB}∕s}$. Donc au total, le processus prendra $\frac{x}{4\mathrm{MB}∕s}+5s+\frac{x}{2\cdot 1\mathrm{MB}∕s}$. L’énoncé nous dit que ce temps doit être égal au temps sans compression. On peut donc égaliser les deux expressions et résoudre l’équation suivante :

La taille du fichier est donc de $20\mathrm{MB}$.

Résultat:

$26$

On remarque d’abord que le périmètre du jardin est égal à la somme des périmètres des rectangles avec les périmètres de $18m$, $20m$ et de celui qui a un point d’interrogation. C’est le cas car on peut déplacer les côtés de ces rectangles pour reformer le rectangle qui correspond au jardin :

Le périmètre du rectangle avec un point d’interrogation doit donc être de $64m-18m-20m=26m$.

Résultat:

$2250$

Plus la distance sur laquelle Adrien freine est grande, moins il a besoin de force. On suppose que la voiture freine à une distance $s=50m$ du cerf. Pour s’arrêter, la voiture doit effectuer un travail pour dépasser la force de freinage, au détriment de son énergie, qui est, dans ce cas l’énergie cinétique.

L’énergie cinétique d’une voiture de masse $m=1000\mathrm{kg}$ et de vitesse $v=15m∕s$ est $E_k=\frac{1}{2}m{v}^2$. Un travail de même intensité doit être fait par la force $F$, avec laquelle la voiture va dépasser la force de freinage. Cette force est effectuée sur une distance $s$, le travail est donc $W=\mathit{Fs}$. On obtient donc l’équation :

L’intensité minimale de la force de freinage agissant sur la voiture doit donc être d’au moins :

Résultat:

$23$

Un prix de $23$ ne peut être payer d’aucune façon avec les pièces qu’on a à disposition. On peut utiliser $0$ ou $1$ pièce de $13$, car si on en utilise plus, le prix serait plus grand que $23$. Dans les deux cas on ne peut pas payer le reste avec des pièces de $3$. On peut toutefois payer tous les prix au-dessus. On commence avec $24$ ($3+3+3+3+3+3+3+3$), $25$ ($13+3+3+3+3$) et $26$ ($13+13$). Si on peut payer trois prix d’affilée, alors on pourra payer également tous les prix plus élevés - il suffira d’ajouter a nombre suffisant de pièces de $3$.

Le prix le plus élevée que Michelle ne peut pas payer sans recevoir de change du caissier est donc de $23$.

Résultat:

$20,25$

Toute la situation est symétrique axialement selon l’axe connectant les deux balles. Cela sera le cas même après la collision, quand les deux balles formeront une plus grande masse. Mais si cette masse bouge à droite où à gauche, la situation ne serait plus symétrique. La masse finale va donc rester immobile.

Au moment de l’impact, les deux balles perdent leur énergie cinétique qu’on suppose entièrement convertie en chaleur, comme dit dans l’énoncé. Cette chaleur est transmise à la masse, qui va chauffer. Chaque masse (qui pèse $m=200g$ et va à une vitesse $v=20m∕s$) a une énergie cinétique $E_k=\frac{1}{2}m{v}^2$. Ensemble, elles auront une énergie cinétique $2E_k=m{v}^2$. C’est cette énergie qui est fournie à la masse finale sous forme de chaleur. Sa masse est de $2m$ (car elle contient les deux balles de masse $m$), sa capacité de chaleur spécifique est $c=800J∕(\mathrm{kg}{}^{\circ }C)$ et elle change d’une température $\mathrm{\Delta }t$. On a l’égalité suivante qui est vérifiée :

Si la température des balles avant la collision était de $t=20{}^{\circ }C$, alors la température de la masse après la collision sera de :

Résultat:

$20$

Pour que la balance soit équilibrée, il faut que les moments agissant sur les deux côtés de la balances soient égaux. Danielle pèse $m=50m$, et est assise à une distance $r=40\mathrm{cm}$ du point de rotation. Une force gravitationnelle $F_g=\mathit{mg}$ agit sur Danielle. C’est avec une force de même intensité que Danielle agit sur la balance, et cette forge agit avec un moment :

Les cubes de l’autre côté de la balance doivent agir avec le même moment. Supposons que nous avons $n$ cubes. L’énoncé du problème nous donne que chaque cube a une masse $m_0=1\mathrm{kg}$ et une longueur de côté $a=10\mathrm{cm}$. Leur masse totale est de $n{m}_0$ et forme un rectangle de longueur $\mathit{na}$. Son centre de masse est à $\frac{\mathit{na}}{2}$ du point de rotation de la balance, donc c’est à cette distance que la force gravitationnelle du rectangle va agir sur la balance. Le moment du rectangle sur la balance est donc de :

Les moments $M_1$ et $M_2$ doivent être égaux. En comparant les deux équations obtenues pour $M_1$ et $M_2$ on obtient :

Le nombre de cubes que Nina a dû mettre sur la balance est donc :

Résultat:

$190$

Réfléchissons d’abord aux chiffres qui peuvent être à la place des unités. Les chiffres $2$, $4$ et $6$ ne peuvent pas être à cette place car le nombre formé serait divisible par $2$, et donc ne serait pas un nombre premier. Pour une raison analogue, $5$ ne peut pas être à la place des unités afin d’éviter que le nombre soit divisible par $5$. On peut donc dire que les chiffres $2$, $4$, $5$ et $6$ seront à la place des unités et les autres chiffres ($1$, $3$, $7$ et $9$) à la place des dizaines. La seule somme qu’on peut obtenir est donc $20+40+50+60+1+3+7+9=190$.

Remarque : Les cartes peuvent vraiment être utilisées pour former 4 nombres premiers à deux chiffres, par exemple $23$, $41$, $59$ et $67$.

Résultat:

$21$

Des droites dans le plan qui ne partagent aucun point commun sont parallèles. On cherche donc à calculer le nombre de paires de droites parallèles qui passent par les 7 point marqués.

Notons $A$, $B$, $C$, $D$, $E$, $F$ et $G$ les points que Tim a marqué. Commençons par trouver les droites qui sont parallèles à $\mathit{AB}$. Ce sont les droites $\mathit{CG}$ et $\mathit{DF}$. Ce sont ces deux droites car un heptagone est symétrique par rapport à la médiatrice du segment $\mathit{AB}$. À partir de cette symétrie, les droites $\mathit{AB}$, $\mathit{CG}$ et $\mathit{DF}$ sont perpendiculaires à la médiatrice de $\mathit{AB}$, et sont donc parallèles entre elles. Nous obtenons donc $3$ paires de droites parallèles.

En répétant le même raisonnement pour les autres lignes, on obtient $3$ paires de droites parallèles à chaque fois.

Chaque droite déterminée par les points $A$ à $G$ est rendue parallèle à l’une des droites $\mathit{AB}$, $\mathit{BC}$, $\mathit{CD}$, $\mathit{DE}$, $\mathit{EF}$, $\mathit{FG}$ et $\mathit{AG}$ (ces $7$ lignes se croisent deux à deux). Donc, de cette façon, nous obtenons toutes les paires de lignes parallèles.

Au total, Tim peut dessiner les deux paires de ligne de $7\cdot 3=21$ manières différentes.

Résultat:

$6$

L’énergie potentielle de la balle quand elle est jetée est de $E_p=\mathit{mgh}$, où $m=60g$ est sa masse, $h=1m$ est la hauteur de laquelle Sophie jette la balle et $g$ est l’accélération gravitationnelle. Avec $v=4m∕s$, l’énergie cinétique au moment du lancer est $E_k=\frac{1}{2}m{v}^2$. Tout le long du mouvement, l’énergie totale de la balle reste conservée. Donc la somme $E_p+E_k$ est constante à tout moment, en particulier au moment où la balle touche le sol. À ce moment-là, la balle est à une hauteur 0, donc son énergie potentielle est nulle. Son énergie totale est donc égale à l’énergie cinétique. Si on note $u$ l’énergie cinétique de la balle juste avant de toucher le sol, on obtient l’équation :

La vitesse de la balle juste avant l’impact est donc

Résultat:

$468$

Le seul nombre à un chiffre qui est égal à la somme de ses chiffres multiplié par $13$ est le nombre $0$. Même si on le compte parmi les nombres naturels (dans certaines branches des mathématiques $0$ est considéré comme un nombre naturel, et d’en d’autres non), cela ne changera pas la somme des nombres que Jonas a trouvé.

Si Jonas trouve un nombre à deux chiffres qui correspond à son critère, on peut l’écrire sous la forme $10A+B$, où $A$ et $B$ sont les chiffres d’un nombre $\mathit{AB}$. Toutefois la multiplication par $13$ de la somme de ces chiffres est $13(A+B)$, et $13(A+B)=13A+13B>10A+B$. Treize fois la somme des chiffres d’un nombre à deux chiffres ne sera jamais égale au nombre lui-même.

On continue avec les nombres à trois chiffres, qui peuvent être écrit sous la forme $100A+10B+C$. Comme c’est un nombre à trois chiffre, $A\ge 1$. La condition sur la somme de ses chiffres nous amène à la relation suivante :

Si $A=1$, alors on a trois possibilités pour les chiffres $B$ et $C$. Les valeurs de $(B,C)$ sont $(1,7)$, $(5,6)$ et $(9,5)$, ce qui correspond aux nombres $117$, $156$ et $195$. On a pas d’autres options pour $A$ car $A\ge 1$, pour $A\ge 2$ nous aurions $29A\ge 58$ et en même temps, on sait que à droite on a $B+4C\le 9+4\times 9=$45. Pour les autres possibilités, il n’y a pas de combinaison de nombres pour lesquels $29A=B+4C$ soit vrai. Cela résout donc le cas des nombres à trois chiffres.

La somme maximale des chiffres d’un nombre à 4 chiffres est $4\cdot 9=36$, donc $13$ fois cette somme sera toujours plus petite que $13\cdot 36<20\cdot 50=1000$ (évidemment, on pourrait aussi compter combien font $13\cdot 36$, mais même une large estimation ne serait pas suffisante pour tirer la conclusion suivante). On peut donc dire que $13$ fois la somme des chiffres ne sera jamais égale à un nombre à 4 chiffres. Jonas n’a donc pas pu trouver de nombre à 4 chiffres ou plus qui vérifient la condition.

Au total, Jonas trouve des nombres dont la somme est $117+156+195=$468.

Résultat:

$8$

Les deux diagonales d’un carré ont la même longueur et sont mutuellement perpendiculaires. On sait que la longueur d’une diagonale du panneau est de $12\mathrm{dm}$. Chacune des diagonales divise le carré en deux triangles, dont la hauteur est égale à la moitié de l’autre diagonale. Chacun de ces triangles a une aire de $12\mathrm{dm}\cdot 6\mathrm{dm}:2=36{\mathrm{dm}}^2$. Le panneau entier est constitué de deux triangles de ce type, son aire est donc de $2\cdot 36{\mathrm{dm}}^2=72{\mathrm{dm}}^2.$

La partie jaune représente $\frac{8}{9}$ du panneau entier, donc son aire est $\frac{8}{9}\cdot 72{\mathrm{dm}}^2=64{\mathrm{dm}}^2$. Son côté a donc une longueur de $\sqrt{64{\mathrm{dm}}^2}=8\mathrm{dm}$.

Résultat:

$48$

Notons $d$ la longueur du tapis roulant. En partant du cas où Jerry ne se tient que sur le tapis, on peut trouver sa vitesse. Il lui faut $t_1=30s$ pour atteindre l’autre extrémité du tapis, donc la vitesse du tapis est $v_{\mathit{tapis}}=\frac{d}{t_1}$. De même, à partir du cas où Jerry marche le long du tapis roulant, nous pouvons trouver la vitesse de Jerry. Elle lui faut $t_2=20s$ pour parcourir la distance, donc sa vitesse est $v_{\mathit{Jerry}}=\frac{d}{t_2}$.

Lorsque Jerry marche dans la direction opposée au mouvement du tapis, sa vitesse est de $v_{\mathit{Jerry}}-v_{\mathit{tapis}}$. Par conséquent, elle marche jusqu’au bout du tapis en :

Dans le cas où Jerry marche dans le sens du tapis roulant, sa vitesse est de $v_{\mathit{Jerry}}+v_{\mathit{tapis}}$. Elle atteint l’autre extrémité du tapis en :

Nous en déduisons que si Jerry marche dans la direction opposée au mouvement du tapis roulant, le temps de trajet est rallongé de :

Résultat:

$8$

Comprenons d’abord à quoi ressemblent les ensembles $A$ et $B$. La fonction $|a|$, également appelée valeur absolue, donne la distance du nombre $a$. Peut-être que ce n’est pas clair à première vue d’après la définition dans la note du problème, mais les valeurs absolues effacent le signe de $a$. Regardez $|x|+|y|$, si $x\ge 0$ et $y\ge 0$. Dans ce cas, $|x|+|y|=x+y$. La condition $|x|+|y|=3$ est alors la même que $x+y=3$, donc $y=3-x$. On a donc une droite contenant les points $(3,0)$ et $(0,3)$. Mais nous sommes dans le cas $x\ge 0$ et $y\ge 0$ ce n’est qu’un segment de droite reliant ces deux points. Pour les autres cas de signes de $x$ et $y$ on obtient que l’ensemble $A$ est constitué des segments reliant les points $(3,0)$ et $(0,3)$, les points $(0,3)$ et $(-3,0)$, les points $(-3,0)$ et $(0,-3)$ les points $(0,-3)$ et $(3,0)$. Il s’agit, en fait, d’un carré dont les sommets sont situés aux points $(0,3)$, $(3,0)$, $(0,-3)$ et $(-3,0)$.

Continuons avec l’ensemble $B$. Il est décrit par la relation $\text{max}\{|x|,|y|\}=2$. Cette fonction, appelée maximum, est égale au plus grand des nombres $|x|$ et $|y|$. Pour que cette fonction soit égale à $2$, il faut qu’au moins un des $|x|$ et $|y|$ soit égal à $2$ et que l’autre soit plus petit. Si $|x|=2$ alors $x=2$ ou $x=-2$. Dans ce cas, on doit avoir $|y|\le 2$, ce qui signifie que $-2\le y\le 2$. Pour $x=2$, cette condition est satisfaite pour les points du segment de droite reliant les points $(2,2)$ et $(2,-2)$, alors que pour $x=-2$, elle est satisfaite pour les points du segment reliant les points $(-2,2)$ et $(-2,-2)$. Nous pouvons répéter ces idées pour $|y|=2$. Cela ajoute à l’ensemble $B$ également le segment reliant les points $(-2,2)$ et $(2,2)$ et le segment reliant les points $(-2,-2)$ et $(2,-2)$. Ainsi, l’ensemble $B$ est aussi un carré, mais cette fois avec les sommets $(2,2)$, $(-2,2)$, $(-2,-2)$ et $(2,-2)$.

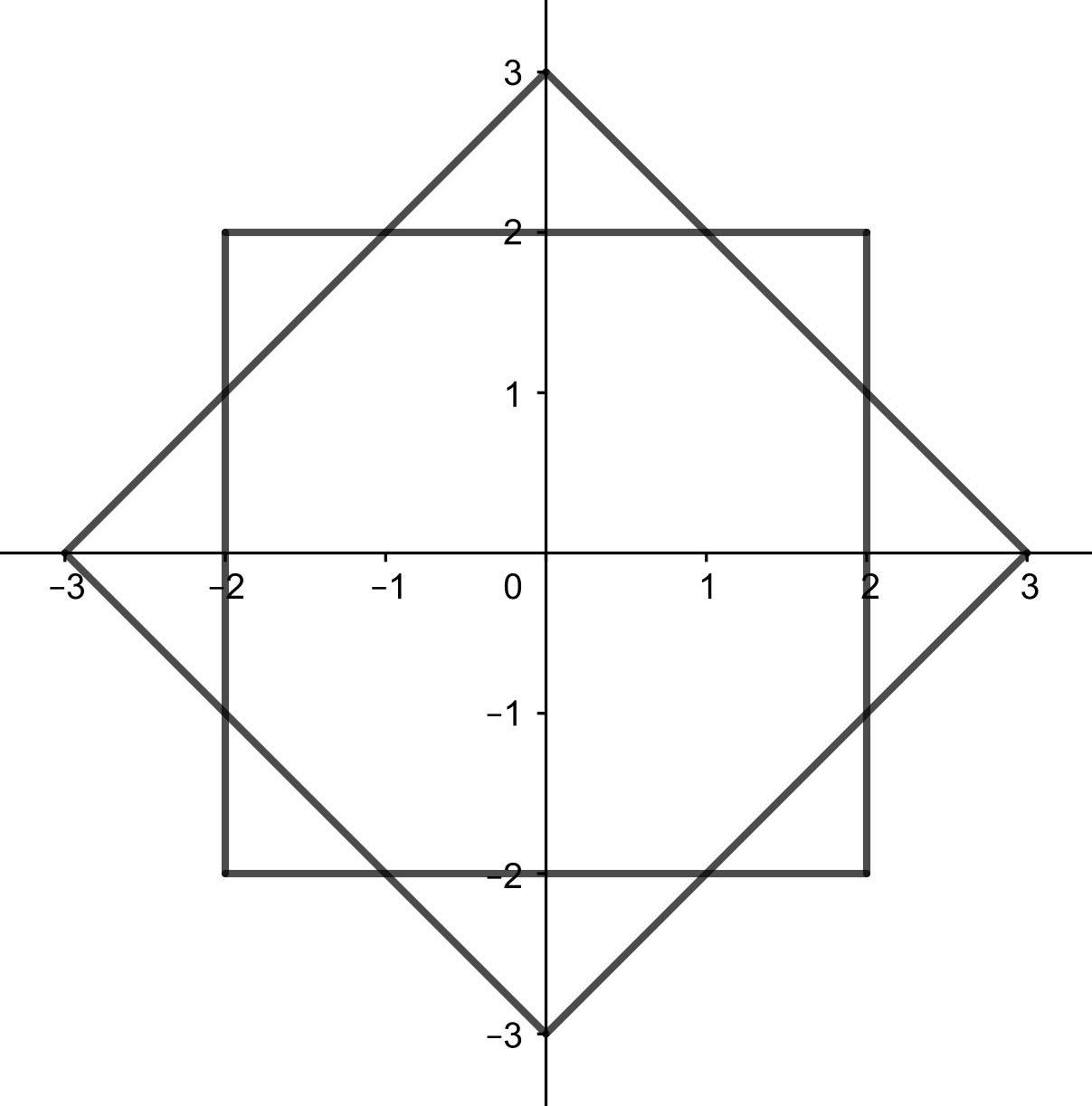
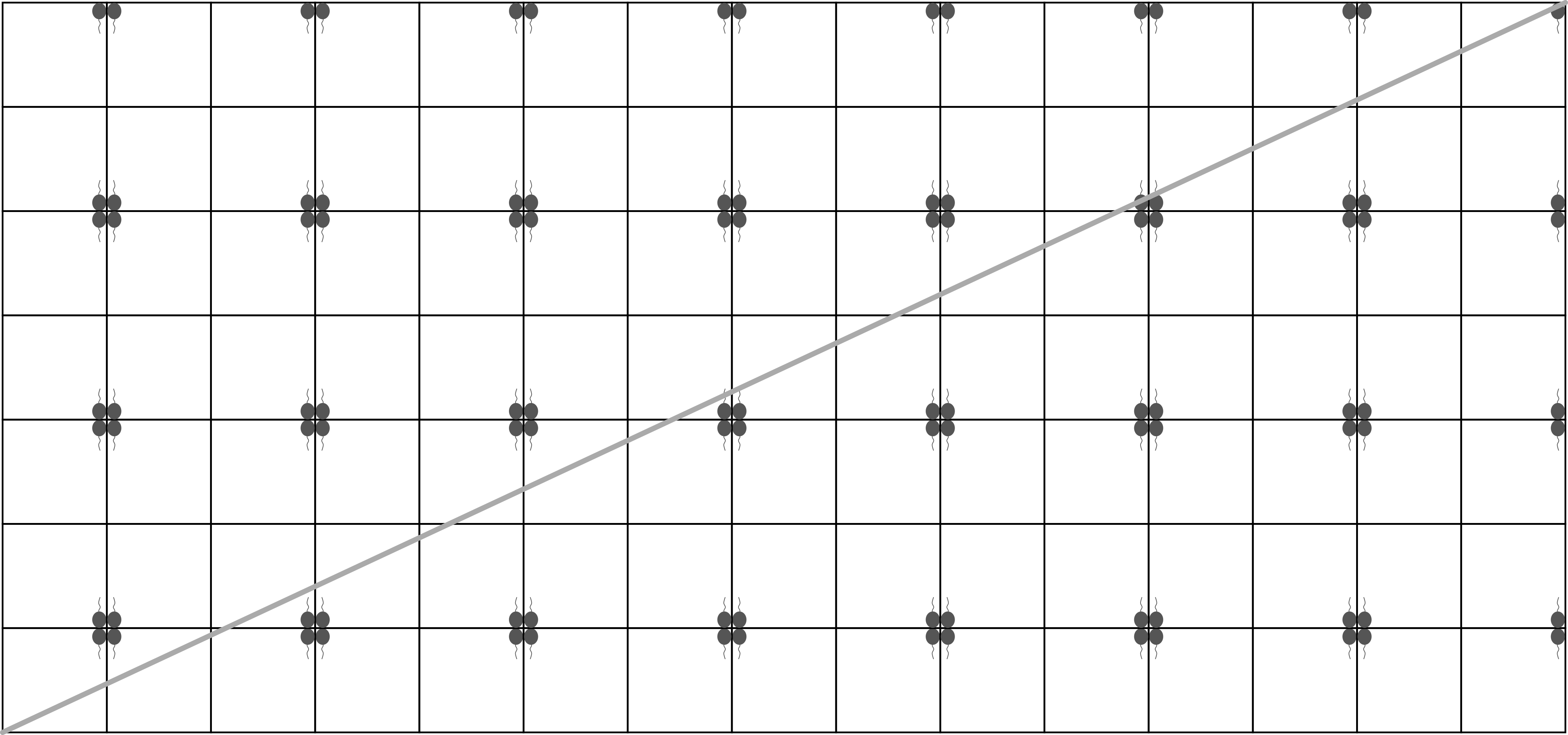
Les ensembles $A$ et $B$ sont dessinés sur la figure suivante :

D’après la figure, on voit que les carrés correspondant aux ensembles $A$ et $B$ se coupent en $8$ points, il y a donc $8$ points qui se trouvent simultanément dans l’ensemble $A$ et l’ensemble $B$.

Résultat:

$9$

Supposons qu’il y ait $a$ résistances dans la branche droite et $b$ résistances dans la branche gauche. Nous devons calculer $\frac{a}{b}$. La résistance des résistances de la branche de droite est de $\mathit{aR}$, où $R=3\mathrm{\Omega }$ est la résistance d’une résistance. Les résistances de la branche de gauche ont une résistance totale de $\mathit{bR}$. La résistance de l’ensemble du composant $R^{\prime }$ est alors :

L’énoncé du problème dit que cette résistance est $10$ fois inférieure à la résistance $\mathit{aR}$ des résistances de la branche de droite. Cela nous donne une équation, à partir de laquelle nous pouvons obtenir la valeur de $\frac{a}{b}$ :

Il y a donc $9$ fois plus de résistances dans la branche de droite que dans la branche de gauche.

Résultat:

$110$

Marianne va effectuer un travail pour soulever une pierre d’une masse de $m=5\mathrm{kg}$ suffisamment haut pour que la pierre entière puisse passer au-dessus du mur. Par conséquent, nous devons déterminer quelle est la hauteur minimale à laquelle nous avons besoin de soulever le centre de masse de la pierre.

Le centre de gravité d’un triangle divise la médiane en deux parties dont les longueurs sont de rapport $2:1$, la partie la plus longue de la médiane étant plus proche du sommet. Dans un triangle équilatéral, chaque médiane est en même temps une hauteur du triangle, ce qui signifie que la médiane a une longueur de $60\mathrm{cm}$. La distance du centre de gravité par rapport à tout côté du triangle est donc de $60\mathrm{cm}:3=20\mathrm{cm}$. Cela signifie que le centre de gravité est au moins à $20\mathrm{cm}$ de tout point du côté du triangle.

Au moment où le centre de gravité d’un triangle (et donc le centre de masse de la pierre) est directement au-dessus du mur, il existe un point situé sur un côté du triangle tel que ce point touche le mur. S’il n’en était pas ainsi, nous pourrions déplacer tout le triangle vers le bas et Marianne fournirait donc moins de travail. Ce point est au moins à $20\mathrm{cm}$ du centre de gravité du triangle. Cela signifie qu’en soulevant la pierre vers le mur, nous devons soulever le centre de gravité d’un triangle approprié (et donc le centre de masse de la pierre) à au moins $20\mathrm{cm}$ au-dessus du mur. Si l’on se demande si cela est possible, on constate que oui - par exemple, en faisant passer la pierre avec une face de la pierre parallèle au sommet du mur (horizontalement).

Cela signifie qu’en passant la pierre au-dessus du mur, Marianne doit soulever le centre de masse de la pierre de $2m$ pour amener le centre de masse au niveau du sommet du mur et de $20\mathrm{cm}$ supplémentaires pour passer la pierre au-dessus du mur. Au total, elle a dû soulever le centre de gravité de $\mathrm{\Delta }h=2m+20\mathrm{cm}=2,2m$, ce qui signifie qu’elle va augmenter l’énergie potentielle de la pierre de $\mathrm{\Delta }{E}_p=\mathit{mg}\mathrm{\Delta }h=5\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 2,2m=110J$. Marianne effectue un travail qui augmente exactement l’énergie potentielle de la pierre de $\mathrm{\Delta }{E}_p$, ce qui signifie que Marianne effectuera un travail de $110J$.

Résultat:

$3$

Notons $A$ et $B$ les deux nombres d’Andréas, alors les nombres écrits au tableau sont $A+B$ et $A-B$. Si l’un des nombres $A$ et $B$ était nul, disons $A=0$, la suite arithmétique serait constituée des nombres $0$, $B$, $B$, $B$. Deux nombres consécutifs de cette suite arithmétique devraient être par exemple $B$ et $B$, et donc, tous les deux nombres consécutifs devraient différer de $B-B=0$. En d’autres termes, tous les nombres de cette suite sont identiques, donc $B=0$. Mais ce cas ne peut pas se produire, puisque $A$ et $B$ doivent être différents.

Nous pouvons continuer en supposant que $A$ et $B$ sont supérieurs à $0$. Nous pouvons également supposer que $A>B$ (dans le cas contraire, nous échangeront simplement $A$ et $B$). En considérant ceci, nous pouvons sans aucun doute dire que le plus grand nombre écrit sur le tableau est $A+B$ et le deuxième plus grand est $A$. Puisque les nombres dans une progression arithmétique doivent continuellement augmenter ou diminuer, les nombres $A+B$ et $A$ sont deux nombres consécutifs dans cette progression. Par conséquent, deux nombres consécutifs doivent différer de $(A+B)-A$ qui est égal à $B$. Par conséquent, le troisième nombre de cette progression doit être $A-B$, un nombre qui est inférieur de $B$ à $A$. Le dernier nombre est $B$, qui doit être plus petit $A-B$ de $B$. Cela nous donne une condition :

Si Andréas choisit les nombres $B$ et $3B$ au départ, après avoir écrit la somme et la différence positive de ces nombres, il obtiendra une progression arithmétique $B$, $2B$, $3B$, $4B$. Il ne reste plus qu’à calculer, dans combien de paires de $A=3B$ et $B$ se trouvent des nombres à un chiffre. Il est facile de vérifier que $A$, $B$ ne peuvent être que $(3,1)$, $(6,2)$ et $(9,3)$. Donc Andréas aurait pu utiliser trois façons de choisir ses nombres.

Résultat:

$4$

Après avoir tiré sur la corde, les poulies libres et le poids se déplacent vers le haut sur une certaine distance. Pendant ce processus, une partie de la corde, qui sort des poulies libres, disparaît, car c’est la partie de la corde qui est passée entre nos mains. L’image montre ce qui se passe après que les poulies aient été soulevées de la ligne pointillée inférieure à la ligne pointillée supérieure - une partie de la corde de même longueur disparaît des cinq parties de la corde entre ces deux lignes. Ainsi, si nous tirons la corde sur une certaine distance, le poids et les poulies libres sont soulevés de telle manière qu’entre les lignes pointillées mentionnées précédemment disparaît la même longueur de corde que celle que nous avons tirée auparavant. Par conséquent, le poids se déplace toujours d’un cinquième de la longueur de la corde que nous avons tirée. Si nous tirons la corde à une vitesse constante de $20\mathrm{cm}∕s$, alors le poids est soulevé à une vitesse de $\frac{20\mathrm{cm}∕s}{5}=4\mathrm{cm}∕s$.

Résultat:

$1290$

Rappelons comment on calcule le plus petit commun multiple et le plus grand commun diviseur. Tout d’abord, nous devons trouver la factorisation en facteurs premiers des nombres. Nous faisons ce qui suit pour chaque facteur premier : dans le plus petit commun multiple, nous mettons ce nombre premier autant de fois qu’il est dans le nombre dans lequel il est le plus de fois. Dans le plus grand diviseur commun, nous le mettons autant de fois qu’il est dans le nombre, dans lequel il est le moins de fois. De là, on peut voir que l’égalité $\text{PPCM}(a,b)\cdot \text{PGCD}(a,b)=a\cdot b$ doit être vérifiée pour tout entier positif $a$, $b$.

Prenons maintenant comme $a$ et $b$ les deux nombres satisfaisant les conditions de Thomas. Pour ces deux nombres, nous avons $a\cdot b=37800$ et $\text{PPCM}(a,b)=42\cdot \text{PGCD}(a,b)$. En plaçant ces équations dans l’équation du paragraphe précédent, on obtient :

Les deux nombres $a$ et $b$ sont donc des multiples de $30$, nous pouvons donc les écrire sous la forme $a=30A$ et $b=30B$ pour certains entiers positifs $A$ et $B$. Maintenant, essayer de trouver une paire dont la somme maximale est $a+b=30A+30A=30(A+B)$ revient à essayer de trouver une paire $A$ et $B$ dont la somme maximale est $A+B$. Puisque le plus grand diviseur commun des nombres $30A$ et $30B$ est $30$, le plus grand diviseur commun de $A$ et $B$ doit être $1$. Nous savons également que :

La somme de deux nombres dont le produit est donné est la plus grande, si les nombres diffèrent le plus possible. Leur différence est la plus grande si $A=42$ et $B=1$ (ou l’inverse). Dans ce cas, on a bien $\text{PGCD}(42,1)=1$ et ces deux nombres ont la somme maximale possible $A+B$. Lorsque nous revenons aux nombres $a$ et $b$, nous constatons que la somme des nombres de Thomas est $a+b=30(A+B)=30(42+1)=30\cdot 43=1290$.

Résultat:

$1250$

Regardons comment les forces agissent dans ce problème. Une force gravitationnelle agit sur le pont de poids $m=400\mathrm{kg}$ en son centre. Son intensité est de $F_G=\mathit{mg}=400\mathrm{kg}\cdot 10N∕\mathrm{kg}=4000N$. A part ça, il y a une force de la chaîne qui agit sur le pont. Si le pont ne bouge pas, il ne tourne pas non plus. La condition pour ne pas tourner est que la somme totale des moments des forces agissant sur le pont soit nulle. La force gravitationnelle agissant sur le pont à une distance $r=1,5m$ provoque un moment de force $M=F_{G}r=4000N\cdot 1,5m=6000Nm$. La partie verticale de la force de la chaîne agit à une distance $r^{\prime }=3m$ et doit provoquer un moment de force $M=6000Nm$. Son intensité doit donc être de $F_2=\frac{M}{r^{\prime }}=\frac{6000Nm}{3m}=2000N$. Il y a deux chaînes, donc chacune d’elles doit être étirée dans le sens vertical avec une force $F_1=\frac{F_2}{2}=\frac{2000N}{2}=1000N$.

Nous connaissons la partie de la force qui étire la chaîne dans la dimension verticale. Mais comment trouver la force dans la direction de la chaîne? Notons que le triangle formé par la chaîne, la porte et le pont est semblable au triangle formé par les forces $\overrightarrow{F}$, $\overrightarrow{F_1}$ et la connexion de leurs extrémités. Ainsi, le rapport des grandeurs de $F_1$ et $F$ est donc le même que le rapport de la hauteur de la porte et de la longueur de la chaîne. La longueur de la chaîne peut être calculée en utilisant le théorème de Pythagore : $\sqrt{{(3m)}^2+{(4m)}^2}=5m$. Par conséquent :

Donc chacune des chaîne est étirée avec une force :

Résultat:

$25$

Trouvons d’abord la probabilité que le nombre de $1$ dans le fichier soit un nombre pair. Laissons les $2021$ premiers chiffres être quelconques. Ils peuvent donc contenir soit un nombre impair de $1$, soit un nombre pair de $1$. Le dernier chiffre est soit $0$ soit $1$. En fonction du dernier chiffre, la parité du nombre de $1$ des premiers $2021$ est soit modifiée par l’ajout du dernier chiffre, soit inchangée. Qu’elle change ou non est cependant tout aussi probable, puisqu’elle dépend uniquement du dernier chiffre et que celui-ci est choisi au hasard avec une probabilité de $0,5$ pour changer la parité et une probabilité de $0,5$ pour conserver la parité des $2021$ premiers chiffres.

Considérons maintenant uniquement les ensembles de chiffres qui ont un nombre pair de $1$. Combien d’entre eux ont un nombre de $1$ divisible par quatre? Si le nombre de $1$ écrit est pair, deux situations peuvent se produire : soit il est également divisible par quatre, soit le reste du nombre de $1$ après division par quatre est de $2$. Considérons deux ensembles, $A$ et $B$. Dans l’ensemble $A$ nous mettrons toutes les situations où le nombre de uns est divisible par quatre, et dans l’ensemble $B$ toutes les situations où le reste est $2$. Observez maintenant que nous pouvons choisir une situation dans l’ensemble $A$ et changer tous les $0$ en $1$ et vice versa. Si le nombre de $1$ dans la situation initiale était de $4n$ et le nombre de $0$ était de $2022-4n$, alors après le changement, le nombre de $1$s sera de $2022-4n$ et le nombre de $0$s sera de $4n$. Cependant, le reste de $2022-4n$ après division par quatre est de $2$. Par conséquent, la situation commutée appartiendra à l’ensemble $B$. En changeant à nouveau, nous obtiendrons à nouveau une situation de l’ensemble $A$ (la situation initiale). De cette façon, nous pouvons diviser les situations en paires, une de l’ensemble $A$ et une de l’ensemble $B$. Chaque situation doit appartenir à l’un des groupes, et donc les ensembles $A$ et $B$ doivent contenir le même nombre de situations.

Cela signifie que dans les situations qui ont un nombre pair de $1$, le nombre de situations où le nombre de $1$ est divisible par quatre a une probabilité de $0,5$. Cela signifie que la probabilité que le nombre de $1$ écrits dans le fichier soit divisible par quatre est $0,5.\cdot 0,5=0,25=25\%$.

Résultat:

$20$

Si nous essayons simplement de dessiner les premières réflexions du faisceau, nous pouvons nous rendre compte qu’il faudra relativement beaucoup de réflexions pour toucher le ballon. À chaque fois, nous devons également calculer exactement où le faisceau se reflète, ce qui n’est pas aussi simple. Essayons donc une autre approche.

Au lieu de retourner le faisceau sur la ligne perpendiculaire au mur au point de réflexion, nous allons retourner la pièce entière sur le mur qui a été touché par le faisceau à chaque fois. Supposons donc qu’à droite de notre pièce d’origine se trouve une autre pièce, en miroir, retournée sur le mur commun. Si nous permettons au faisceau de traverser le mur et d’entrer dans la pièce de droite, il se déplacera dans cette pièce miroir de la même manière que le faisceau réfléchi dans la pièce d’origine. En répétant cette manière de retourner la pièce sur le mur qui a été touché par le faisceau, nous pouvons voir que nous avons un faisceau qui se déplace en ligne droite. D’après la première réflexion, nous savons qu’à chaque fois que le faisceau parcourt $3m$ vers la droite, il parcourt également $1,4m$ vers le haut. Au bout d’un certain temps, il touchera l’un des coins du système de pièces réfléchissantes et, avec un peu de chance, ce sera un coin où se trouvera le ballon (ou l’une de ses réflexions).

Un coin est touché par le faisceau lorsque la distance parcourue vers la droite et la distance parcourue vers le haut sont toutes deux un multiple de la longueur $3m$. Si le faisceau parcourt $k\cdot 3m$ vers la droite, nous savons, à partir de la première réflexion, qu’il parcourra $k\cdot 1,4m$. Si $k$ est un nombre entier positif, alors $k\cdot 3m$ est un multiple de la longueur $3m$. Par conséquent, nous devons chercher le plus petit entier positif $k$ pour que $k\cdot 1,4m$ soit aussi un multiple de la longueur $3m$. Puisque $1,4m=\frac{7}{15}\cdot 3m$, le plus petit de ces $k$ doit être $k=15$. La situation est alors représentée sur la figure ci-dessous :

Nous pouvons voir sur la figure que le faisceau frappe réellement le coin avec le ballon. Il ne reste plus qu’à calculer le nombre de réflexions. Dans notre approche, une réflexion par un mur de la pièce d’origine est égale à la ligne droite de notre faisceau traversant un mur des pièces en miroir, sortant dans une pièce adjacente en miroir. Nous pouvons voir que le faisceau sort par le mur droit de n’importe quelle pièce $14$ fois et par le mur supérieur de n’importe quelle pièce $6$ fois. Par conséquent, il traverse un mur $14+6=20$ fois. Dans la pièce d’origine, cela signifie que le faisceau est réfléchi $20$ fois avant de toucher le ballon.

Note : Cette figure montre comment le faisceau se reflète exactement ($20$ fois) avant de frapper le ballon :

Résultat:

$1,5$

Après l’ajout de la farine de masse $m=45g$ dans le petit verre de base d’aire $S=10{\mathrm{cm}}^2$, la force de pesanteur agissant sur ce verre est augmentée de $\mathrm{\Delta }{F}_G=\mathit{mg}$. Pour que le verre flotte encore, la force de flottaison doit avoir été augmentée de la même quantité. La force de flottaison n’a pu augmenter que par l’augmentation de la partie immergée du verre. D’après la poussée d’Archimède : $\mathrm{\Delta }{F}_{\mathit{fl}}=\mathrm{\Delta }{V}^{\prime }{\rho }_{\mathit{eau}}g$, où $\mathrm{\Delta }{V}^{\prime }$ est le changement de volume de la partie immergée. À partir de cela, on obtient :

Pour que le volume d’une partie immergée augmente, le fond du plus petit verre doit descendre plus bas, et donc se rapprocher du fond du plus grand verre d’une certaine hauteur

. Au cours de ce processus, le cylindre d’eau de volume

est gêné dans sa course, et doit donc se déplacer quelque part. Il va se déplacer vers les côtés du plus petit verre. Là, il provoquera l’augmentation de la surface d’eau dans le plus grand verre de

. Le volume d’eau, qui s’est déplacé ici, peut être exprimé par

, où

est l’aire de la base du plus grand verre. Grâce à cela, nous obtenons l’équation :

Au cours de ces mouvements, la hauteur de la partie immergée du plus petit verre augmente de $h+h^{\prime }$ et donc si nous connaissons son volume, nous obtenons également l’équation :

En combinant ces $2$ équations, on obtient :

Donc la hauteur de la surface de l’eau dans le grand verre a augmenté de

Résultat:

$2043$

Ce serait dur de sommer autant de neufs. Il faudrait trouver une autre manière de sommer ces nombres. Remarquons qu’en ajoutant $1$ à chaque nombre, on obtient un nombre qui commence avec un $1$ et qui possède des zéros après. La somme $9+99+999+9999+\dots$ peut alors être réécrite sous la forme $(10-1)+(100-1)+(1000-1)+(10000-1)+\dots$

En sommant tous les $-1$, on obtient $-2022$. Le reste de la somme nous donne $11\dots 110$, avec $2022$ chiffres $1$. Le nombre que Suzanne a obtenu est ce nombre réduit de $2022$.

A quoi ressemble ce nombre? La soustraction de $2022$ n’affecte que les $5$ derniers chiffres du grand nombre. Ces $5$ derniers chiffres deviennent donc $11110-2022=9088$. Les autres $2018$ chiffres du nombre ne sont pas affectés. La somme des chiffres du nombre de Suzanne est donc $2018\cdot 1+9+0+8+8=2043$.

Résultat:

$6,4$

Supposons que les dimensions de la brique soient $a$, $b$, $c$ et que sa masse soit $m$. Alors les pressions $p_1=2400\mathrm{Pa}$, $p_2=3200\mathrm{Pa}$ et $p_3=4800\mathrm{Pa}$ de l’énoncé du problème sont liées par ces équations :

En multipliant ces $3$ équations, on obtient :

Cependant, $\mathit{abc}$ est le volume $V$ de la brique. L’équation du dessus peut être transformée en :

Il suffit de remarquer que la fraction $\frac{m}{V}$ est la densité de la brique $\rho =2400\mathrm{kg}∕m^3$. En utilisant cela, on peut trouver la masse de la brique :

La masse de la brique de Bob le bricoleur est $6,4\mathrm{kg}$.

Résultat:

$588$

Soit $P$ l’intersection des segments $\mathit{AD}$ et $\mathit{BC}$. Puisque les lignes $\mathit{AB}$ et $\mathit{CD}$ sont parallèles, les triangles $\mathit{PAB}$ et $\mathit{PDC}$ sont semblables. Le rapport des longueurs correspondantes de ces triangles est de $\frac{75\mathrm{cm}}{100\mathrm{cm}}=\frac{3}{4}$. Cela donne les relations :

Cependant, on sait que $|\mathit{PA}|=|\mathit{PD}|+|\mathit{AD}|=|\mathit{PD}|+7\mathrm{cm}$ et $|\mathit{PB}|=|\mathit{PC}|+|\mathit{BC}|=|\mathit{PC}|+24\mathrm{cm}$. En utilisant ces deux équations, on obtient :

Dans le triangle $\mathit{PCD}$ on a l’égalité ${(21\mathrm{cm})}^2+{(72\mathrm{cm})}^2={(75\mathrm{cm})}^2$. Par le Théorème de Pythagore, c’est un triangle rectangle avec l’angle droit au sommet $P$. Ainsi, le triangle $\mathit{PAB}$ est également un triangle rectangle. L’aire du trapèze $\mathit{ABCD}$ est égal à la différence des aires de ces deux triangles.

Les côtés du triangle $\mathit{PCD}$ sont de longueur $21\mathrm{cm}$ et $72\mathrm{cm}$, sont son aire est $21\mathrm{cm}\cdot 72\mathrm{cm}:2=756{\mathrm{cm}}^2$. Le triangle $\mathit{PAB}$ possède des côtés de longueur $21\mathrm{cm}+7\mathrm{cm}=28\mathrm{cm}$ et $72\mathrm{cm}+24\mathrm{cm}=96\mathrm{cm}$, donc son aire est $28\mathrm{cm}\cdot 96\mathrm{cm}:2=1344{\mathrm{cm}}^2$.

Ainsi, l’aire du trapèze $\mathit{ABCD}$ est $1344{\mathrm{cm}}^2-756{\mathrm{cm}}^2=588{\mathrm{cm}}^2$.

Résultat:

$1430$

Résolvons d’abord un problème plus facile, dans lequel Tiphaine ne marque que $4$ points. Nommons les points placés $A$, $B$, $C$ et $D$ de telle sorte qu’ils se trouvent sur le cercle dans cet ordre. Les segments dessinés ne doivent pas avoir de points communs, extrémités comprises. Par conséquent, un segment doit avoir ses extrémités dans une paire de points et l’autre segment dans l’autre paire de points. Pour cette raison, les deux segments peuvent être dessinés de trois manières différentes :

1.

les segments $\mathit{AB}$ et $\mathit{CD}$,

2.

les segments $\mathit{AC}$ et $\mathit{BD}$,

3.

les segments $\mathit{AD}$ et $\mathit{BC}$.

Nous pouvons maintenant revenir au problème, dans lequel Tiphaine a $13$ points sur un cercle. La paire de segments aura ses extrémités sur $4$ points distincts. Après avoir choisi ces $4$ points, nous pouvons appliquer ce que nous avons découvert dans le problème simplifié avec seulement $4$ points. Ainsi, après avoir choisi le quadruple des points, nous aurons $2$ façons de dessiner les segments (on avait $3$ choix en tout, mais un des choix donnait lieu à un croisement).

Il reste à calculer le nombre de façons de choisir $4$ points. Pour choisir le premier d’entre eux, nous avons $13$ possibilités, pour choisir le second $12$ possibilités, pour le troisième $11$ de possibilités et pour le quatrième $10$ possibilités. En procédant ainsi, nous avons inclus chaque quadruplet de points plusieurs fois. Plus précisément, nous l’avons inclus une fois pour chaque ordre possible des points qui le composent. Pour la première position, nous avons $4$ possibilités, pour la deuxième $3$, pour la troisième $2$ et pour la dernière $1$. Le nombre de possibilités de choisir les $4$ points est donc $(13\cdot 12\cdot 11\cdot 10):(4\cdot 3\cdot 2\cdot 1)=715$.

Si l’on ajoute à cela le fait que pour chaque quadruplet point, nous avons $2$ façons de dessiner la paire de segments, nous obtenons que Tiphaine peut dessiner les segments de $2\cdot 715=1430$ façons.