Problems and solutions

Résultat:

$27$

Quand Alice donne à Bob onze de ses galets, elle en perd $11$ et Bob en gagne $11$. Ainsi, la différence dans le nombre de galets qu’ils ont diminue de $11+11=22$. Donc, à la fin, Alice aura $49-22=27$ galets de plus que Bob.

Résultat:

$5$

Les trois premiers mois de l’année $2023$ avaient respectivement $31$, $28$ et $31$ jours. Ensemble, ils totalisent $31+28+31=90$ jours, ce qui équivaut à $90\cdot 24=2160$ heures. Tania a donc parcouru $10800\mathrm{km}$ en $2160$ heures. Par conséquent, sa vitesse moyenne doit avoir été de $\frac{10800\mathrm{km}}{2160h}=5\mathrm{km}∕h$.

Résultat:

$56$

Pour dessiner uniquement les quatre carrés du bas, Laura doit dessiner $13$ segments. Pour ajouter les trois carrés suivants, elle dessine 7 segments supplémentaires. Pour ajouter les deux carrés suivants, elle dessine 5 segments de plus. Enfin, pour dessiner le carré du haut, Laura dessine 3 segments. Au total, elle dessine $13+7+5+3=28$ segments. Chacun d’entre eux a une longueur de $2\mathrm{cm}$, donc la longueur totale des segments est de $28\cdot 2\mathrm{cm}=56\mathrm{cm}$.

Résultat:

$45$

En consultant les conversions dans la fiche de formules et constantes, nous trouvons que $36\mathrm{oz}$ équivaut à $1l$. Ainsi, le volume de la canette en litres est $\frac{12\mathrm{oz}}{36\mathrm{oz}∕l}=\frac{1}{3}l$. Par conséquent, il y a $3\cdot 150=450$ kilocalories dans un litre de coca, et $450:10=45$ kilocalories dans $100\mathrm{ml}$.

Résultat:

$7$

Si le coffre avait $48$ pièces de moins, chaque pirate recevrait $6$ pièces de moins que ce qu’il/elle a actuellement. Il doit donc y avoir $48:6=8$ pirates. Comme la question demande combien d’amis pirates Anthony a, la réponse correcte est $8-1=7$.

Résultat:

$4620$

En $18$ minutes, Andréas parcourt $18:3=6$ tours. Chaque tour a une longueur de $2\pi \cdot 70m=140\pi m$. Donc, il parcourt une distance de $6\cdot 140\pi m=840\pi m$, et autant de pas. De la même manière, Zoé parcourt $18:2=9$ tours, chacun de longueur $2\pi \cdot 35m=70\pi m$. Elle parcourt $630\pi m$ et autant de pas. Ainsi, au total, ils font $840\pi +630\pi =1470\pi$ pas. Si nous utilisons l’approximation $\pi =\frac{22}{7}$, nous obtenons qu’ils ont fait $1470\cdot \frac{22}{7}=4620$ pas.

Si nous utilisons la valeur $\pi =3,14$, nous obtiendrons le résultat $4615,8$, ce qui donnerait le même résultat après arrondissement à la dizaine la plus proche.

Résultat:

$9$

Pour ouvrir la porte avec une force minimale, nous devons atteindre l’équilibre du couple. Le couple $M$ du mécanisme de fermeture est égal à sa force multipliée par la distance par rapport aux gonds : $M=48N\cdot 15\mathrm{cm}=720N\mathrm{cm}$. En utilisant la même équation, nous obtenons la force $F$ nécessaire pour ouvrir la porte à la distance $a=80\mathrm{cm}$ :

Résultat:

$6,28$

En supposant que la Terre est une sphère parfaite, une corde enroulée autour de son équateur formera un cercle parfait. En notant le rayon de ce cercle $r$, la corde d’Ève devra mesurer $2\mathit{\pi r}$. Adam, quant à lui, prévoit de former un cercle dont le rayon est $r+1m$. Par conséquent, la corde d’Adam doit mesurer $2\pi (r+1m)$. La différence entre la corde d’Adam et celle d’Ève s’élève donc à $2\pi (r+1m)-2\mathit{\pi r}=2\pi m\doteq 6,28m$.

Résultat:

$5$

Chaque fois que le rayon lumineux touche le miroir, il change de direction de $90^{\circ }$, soit vers la droite, soit vers la gauche (en fonction de l’orientation du miroir). Il est facile de trouver une configuration des miroirs où seules $5$ réflexions sont nécessaires (l’orientation des miroirs dans les carrés vides n’a pas d’importance) :

D’autre part, il est facile de voir que le chemin le plus court passant par $3$ carrés est impossible (le rayon ne changerait pas de direction dans plusieurs carrés). De plus, on peut voir qu’il doit y avoir un nombre impair de réflexions - après chaque réflexion de nombre impair, le rayon va dans la direction verticale (et après chaque réflexion de nombre pair, il va dans la direction horizontale).

Ainsi, le nombre de réflexions doit être un nombre impair supérieur à $3$, ce qui signifie que $5$ est effectivement le nombre minimal de réflexions.

Résultat:

$45$

Si nous utilisons uniquement le chiffre $1$, nous obtenons $5$ nombres "durs" dans l’intervalle donné : $11$, $111$, $1111$, $11111$ et $111111$. De la même manière, nous obtenons $5$ nombres "durs" pour chacun des chiffres de $2$ à $9$, et nous n’obtenons aucun nombre "dur" avec le chiffre $0$. Par conséquent, il y a $9\cdot 5=45$ nombres "durs" supérieurs à dix et inférieurs à un million.

Résultat:

$1$

La somme de tous les chiffres écrits sur le tableau est $0+1+2+3+4+5+6=21$. Cela signifie que la somme des chiffres dans chaque colonne doit être $21:3=7$. Ensuite, le chiffre $0$ ne peut pas être dans la première ou la dernière colonne, car nous aurions besoin d’utiliser le chiffre $7$, que nous n’avons pas. Ainsi, le chiffre $0$ sera utilisé dans la colonne du milieu, ce qui force le produit des chiffres dans la colonne du milieu à être toujours $0$. Par conséquent, Daniel ne peut obtenir qu’un seul résultat, à savoir $0$.

Résultat:

$250$

Si Pierre n’avait pas oublié de boucher le clapet, la baignoire se serait remplie en $150l:0,2l∕s=750s$. Mais Pierre a oublié de boucher le clapet, ce qui a réduit le débit d’arrivée de l’eau à $0,2l∕s-0,05l∕s=0,15l∕s$. La baignoire se remplira maintenant en $150l:0,15l∕s=1000s$, de sorte que le temps nécessaire pour remplir la baignoire sera de $1000s-750s=250s$ de plus.

Résultat:

$16$

Après le premier mouvement, le roi peut se déplacer vers l’une des cases comme dans cette figure :

Maintenant, la question est de savoir combien de cases le roi peut atteindre à partir de n’importe laquelle des positions de la figure précédente. Nous trouvons facilement que le roi peut se déplacer vers l’une de ces $16$ cases :

Résultat:

$14$

Les deux nouveaux triangles partagent deux côtés avec le quadrilatère original et ont un côté de longueur égale à la diagonale. Cela signifie que le nouveau périmètre est égal à la somme des périmètres, plus deux fois la longueur de la diagonale. Comme le périmètre a augmenté de $77\mathrm{cm}-49\mathrm{cm}=28\mathrm{cm}$, la longueur de la diagonale est de $28\mathrm{cm}:2=14\mathrm{cm}$.

Résultat:

$10$

Après le lancer, la composante horizontale de la vitesse de la balle sera de $9\mathrm{km}∕h=2,5m∕s$ tandis que Sophie accélère à une vitesse de $18\mathrm{km}∕h=5m∕s$. Par conséquent, la vitesse relative entre Sophie et la balle sera de $5m∕s-2,5m∕s=2,5m∕s$. Par conséquent, après $4$ secondes, le moment où la balle touche le sol, Sophie sera à une distance de $2,5m∕s\cdot 4s=10m$.

Résultat:

CDAB

Dans la première étape, nous allons essayer de trouver la position d’Alice. Puisque toutes les déclarations sont fausses, Alice ne peut pas être la deuxième. Béatrice et Charlotte sont arrivées après et avant Alice, respectivement. Cela signifie qu’au moins une fille est à la fois avant et après Alice, ce qui rend impossible pour Alice d’être la première ou la quatrième. La seule possibilité pour elle est d’être arrivée en troisième. La déclaration fausse de Béatrice selon laquelle elle est arrivée avant Alice implique qu’elle doit être après Alice, ce qui en fait la dernière. Daisy n’est pas arrivée en première, ce qui lui laisse la deuxième place, car les troisième et quatrième positions sont déjà prises. Dans la dernière étape, nous attribuerons Charlotte à la première place, le seul emplacement libre restant, et il est clair que sa déclaration correspond à sa position. Par conséquent, l’ordre final d’arrivée est : Charlotte, Daisy, Alice, Bella (CDAB).

Résultat:

$5$

Calculons l’intervalle de passage du tramway $12$. Lorsque Jean voyage en tramway, sa vitesse relative par rapport aux tramways en direction opposée est deux fois plus rapide que la vitesse réelle des tramways. Cela signifie qu’il voit que la distance constante entre deux tramways consécutifs est parcourue deux fois plus rapidement. Par conséquent, l’intervalle réel de desserte de l’arrêt est deux fois plus long que l’intervalle auquel Jean observe les tramways en direction opposée. Ainsi, le tramway $12$ dessert l’arrêt toutes les $2\cdot 2=4$ minutes. En une heure, $60:4=15$ tramways $12$ desserviront l’arrêt.

De même, $60:6=10$ tramways $5$ desserviront l’arrêt en une heure. Par conséquent, le tramway $12$ dessert l’arrêt $15-10=5$ fois de plus que le tramway $5$.

Résultat:

$250$

Nous devons réfléchir à la manière dont le frottement affecte la boîte. La force de frottement n’agit que entre les solides qui agissent sur eux-mêmes avec une certaine force de pression. Mais dans notre cas, la boîte n’exerce aucune pression sur le mur vertical. Par conséquent, aucune force de frottement n’agit sur la boîte. Cela signifie que la seule force (à l’exception de celle de Bob) agissant sur la boîte est la force gravitationnelle $F_g=\mathit{mg}$, où $m=25\mathrm{kg}$ est la masse de la boîte. Bob doit agir avec une force $F$ de la même magnitude, il doit donc tirer sur la corde avec une force $F=\mathit{mg}=25\mathrm{kg}\cdot 10N∕\mathrm{kg}=250N$.

Résultat:

$50$

Les exigences de Caroline sont de prendre au moins $2$ pots de confiture de framboises, $5$ pots de confiture de myrtilles, $1$ pot de confiture de mûres, $1$ pot de confiture de groseilles et $1$ pot de confiture de fraises. Nous allons réfléchir à ce qui pourrait se passer si certaines de ces exigences ne sont pas remplies. Le pire scénario possible qui empêcherait Caroline d’avoir $2$ pots de confiture de framboises est qu’elle prenne tous les pots de différents types, sauf $1$ pot de confiture de framboises. Au total, cela ferait $1+15+7+15+9=47$ pots de confiture. Cependant, si elle en prend $48$, ce problème ne se poserait pas. De la même manière, le problème serait de prendre $4$ pots de confiture de myrtilles et tous les pots des autres types, ce qui ferait un total de $10+4+7+15+9=45$ pots de confiture. Par conséquent, elle doit prendre au moins $46$ pots de confiture. En appliquant la même idée aux mûres, aux groseilles et aux fraises, nous constatons qu’il n’y aurait pas de problème si Caroline prenait au moins $(10+15+0+15+9)+1=50$, $(10+15+7+0+9)+1=42$ ou $(10+15+7+15+0)+1=48$ pots de confiture, respectivement. En combinant tout cela, nous découvrons que les exigences seront satisfaites si le nombre de pots de confiture pris est le plus élevé parmi les nombres $48$, $46$, $50$, $42$, $48$. Par conséquent, Caroline doit prendre $50$ pots de confiture.

Résultat:

$64$

Soit $s$ la longueur du circuit et $t$ le temps du vainqueur à l’arrivée. Nous savons que la vitesse moyenne du vainqueur était de $24\mathrm{km}∕h$, donc $\frac{s}{t}=24\mathrm{km}∕h$.

Les deux tiers de la distance de la course étaient en descente, donc la longueur des descentes est $\frac{2}{3}s$. De plus, le vainqueur a passé $3$ fois plus de temps dans les montées. Par conséquent, il a passé un temps $\frac{1}{4}t$ dans les descentes. La vitesse moyenne du vainqueur dans les descentes est donc :

En remplaçant $\frac{s}{t}=24\mathrm{km}∕h$, nous trouvons que la vitesse moyenne du vainqueur dans les descentes est :

Résultat:

$95$

Regardons la dernière ligne et la deuxième colonne. Elles doivent avoir la même somme, mais elles partagent également une case en commun. Par conséquent, elles doivent également avoir la même somme pour les nombres qui ne sont pas en commun. Par conséquent, la somme des nombres $15$ et $19$ doit être la même que la somme du nombre $16$ et du nombre dans la case du milieu. Cette somme est $15+19=34$, ce qui signifie que le nombre dans la case du milieu doit être $34-16=18$.

Maintenant, nous avons tous les nombres sur l’une des diagonales. Par conséquent, la somme des nombres dans chaque ligne, chaque colonne et sur les deux diagonales doit être $17+18+19=54$. À partir de là, il est facile de compléter l’ensemble du tableau.

Enfin, nous calculons que la somme des nombres manquants est $21+22+18+14+20=95$.

Résultat:

$0,8$

Nous pouvons remplacer chaque $1m$ de fil par une résistance ayant une résistivité de $R_0=0,1\mathrm{\Omega }$. Si nous faisons cela, nous obtenons le schéma suivant :

Maintenant, nous pouvons utiliser les formules pour les résistances connectées en série et en parallèle. Nous obtenons que la résistivité entre les points $A$ et $B$ est :

Résultat:

$5$

Un volume $V=150\mathrm{hl}$ d’eau a une masse $m=V{\rho }_{\mathit{water}}$. Pour la chauffer de la température $t_1=29\circ C$ à $t_2=33\circ C$, nous devons lui ajouter la chaleur $Q=c_{\mathit{water}}m(t_2-t_1)=c_{\mathit{water}}V{\rho }_{\mathit{water}}(t_2-t_1)$. Cette chaleur doit être égale au travail exercé par les panneaux solaires. Ils ont une puissance $P_0=1,4\mathrm{kW}∕m^2$ par unité de surface, donc si la surface totale des panneaux solaires est $S$, ils ont une puissance $P=P_{0}S$. Après un certain temps $t=10h$, ils exerceront le travail $W=\mathit{Pt}=P_0\mathit{St}$. C’est le travail exercé sur l’eau, donc nous devons avoir :

Ainsi, Ann a besoin de $5m^2$ de panneaux solaires.

Résultat:

$40$

Nous pouvons représenter l’ordre des buts avec une chaîne de P et de M, où P représente un but marqué par les physiciens et M un but marqué par les mathématiciens. Avec cette notation, nous pouvons voir qu’il y a $10$ ordres possibles dans lesquels les buts de la première mi-temps ont pu être marqués : MMPPP, MPMPP, MPPMP, MPPPM, PMMPP, PMPMP, PMPPM, PPMMP, PPMPM, PPPMM. En suivant une procédure similaire pour les $4$ buts restants de la deuxième mi-temps, nous trouvons qu’il y avait $4$ ordres possibles : PMMM, MPMM, MMPM, MMMP. Comme la première et la deuxième mi-temps sont des parties indépendantes du match, n’importe quel ordre des buts de la première mi-temps peut être associé à n’importe quel ordre des buts de la deuxième mi-temps. Par conséquent, le nombre total de manières possibles dont tous les buts ont été marqués est de $10\cdot 4=40$.

Résultat:

$125$

Si le robot pousse avec une force $F$ de chaque côté, alors la force de frottement de chaque côté est $F_f=\mathit{fF}$ et elle est dirigée vers le haut, où $f$ est le coefficient de frottement $f=0,3$. D’autre part, la force gravitationnelle $F_g=\mathit{mg}$ agit sur le robot vers le bas. Pour que le robot reste stable, la force gravitationnelle doit être égale à la somme des quatre forces de frottement. Donc, nous devons avoir :

Par conséquent, la force $F$ doit être :

Résultat:

$3$

Chaque hexagone peut être divisé en $6$ triangles équilatéraux. Cela nous permet de dessiner une grille triangulaire sur la figure :

À partir de là, nous voyons immédiatement que la longueur du côté de l’hexagone (qui est la même que la longueur du côté des triangles) est de $12\mathrm{cm}:4=3\mathrm{cm}$.

Résultat:

$1100$

Le navire sombrera complètement lorsque la force gravitationnelle sera égale à la force de flottabilité. La force de flottabilité maximale qui peut agir sur le navire avec un volume $V$ est $F_{\mathit{buoy}}=V{\rho }_{\mathit{water}}g$. La force gravitationnelle se compose de deux parties : la force gravitationnelle du navire lui-même et la force gravitationnelle de l’eau qui a coulé dans le navire. La force gravitationnelle du navire avec une masse $m$ est $F_{g_1}=\mathit{mg}$. L’eau coule dans le navire avec un débit $Q$, donc après un certain temps $t$, il y aura un volume $V^{\prime }=\mathit{Qt}$ d’eau dans le navire. Donc, sa force gravitationnelle sera $F_{g_2}=\mathit{Qt}{\rho }_{\mathit{water}}g$. La condition pour la submersion est $F_{\mathit{buoy}}=F_{g_1}+F_{g_2}$, à partir de laquelle nous pouvons exprimer le temps $t$ :

Par conséquent, le navire sombrera complètement après un certain temps :

Résultat:

$1990$

Les deux amies ont ajouté les années de leur naissance au nombre $2023$. Emily a obtenu un résultat supérieur, elle a donc ajouté certaines années que Amily n’a pas incluses. Étant donné que chaque sommande est d’environ $2000$, le nombre de sommes ajoutées uniquement par Emily est de $19945:2000\doteq 10$. Cela signifie que les années ajoutées uniquement par Emily sont $x$, $x+1$, …, $x+9$, où $x$ est l’année de naissance d’Emily. Leur somme est $10x+45$. Ainsi, nous obtenons l’équation $10x+45=19945$ à partir de laquelle nous découvrons qu’Emily est née en l’an $x=\frac{19945-45}{10}=1990$.

Résultat:

$11$

Essayez les possibilités en fonction de l’orientation du premier et du dernier miroir. En fonction d’eux, nous obtenons les rangées de la figure suivante (pour une meilleure compréhension, nous ne dessinons pas les rayons et les miroirs dont l’orientation est immatérielle) :

Donc, nous constatons qu’il existe $1+3+3+4=11$ trajectoires possibles du rayon lumineux.

Résultat:

$\frac{68}{3}$

Soient les longueurs des côtés du rectangle $\mathit{ABCD}$ égales à $\mathit{AB}=9x$ et $\mathit{BC}=8x$ pour un certain $x$.

Tout d’abord, calculons le périmètre du quadrilatère $\mathit{ABEF}$. Les côtés du triangle rectangle $\mathit{ECF}$ ont des longueurs de $4x$ et $3x$. Ainsi, le triangle de Pythagore donne $\mathit{EF}=\sqrt{{(4x)}^2+{(3x)}^2}=5x$. De même, le triangle rectangle $\mathit{FDA}$ a des côtés de longueurs $6x$ et $8x$, donc $\mathit{FA}=\sqrt{{(6x)}^2+{(8x)}^2}=10x$. Par conséquent, le périmètre du quadrilatère est de $9x+4x+5x+10x=28x$.

Maintenant, calculons la surface du quadrilatère $\mathit{ABEF}$. Les triangles rectangles $\mathit{ECF}$ et $\mathit{FDA}$ ont des aires de $\frac{(4x)\cdot (3x)}{2}=6x^2$ et $\frac{(6x)\cdot (8x)}{2}=24x^2$. L’aire du rectangle $\mathit{ABCD}$ est $(9x)\cdot (8x)=72x^2$, donc l’aire du quadrilatère $\mathit{ABEF}$ est de $72x^2-6x^2-24x^2=42x^2$.

Nous savons que les valeurs numériques du périmètre et de la surface du quadrilatère $\mathit{ABEF}$ sont les mêmes, ce qui signifie :

Il reste à calculer le périmètre du rectangle $\mathit{ABCD}$, qui est de $9x+8x+9x+8x=34x=34\cdot \frac{2}{3}\text{ cm}=\frac{68}{3}\text{ cm}$.

Résultat:

$2$

Le travail du ver sera l’énergie potentielle maximale du ver pendant son ascension sur le cube (en supposant que son énergie potentielle est initialement nulle). Il est facile de voir que le maximum sera atteint précisément au moment où le ver se trouvera dans la position indiquée dans l’image de l’énoncé (plus ses parties sont élevées, plus son énergie potentielle est élevée).

Divisez le ver en 3 parties (ne vous inquiétez pas, elles se régénéreront) - deux parties verticales et une horizontale comme indiqué dans l’image de l’énoncé. Elles ont toutes une longueur de $10\mathrm{cm}$, soit un tiers de la longueur totale du ver. Le ver étant homogène, ces 3 parties ont une masse de $m_0=1g$. La partie horizontale a son centre de gravité à une hauteur de $h_2=10\mathrm{cm}$, donc l’énergie potentielle de cette partie est de $E_2=m_{0}g{h}_2=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,1m=0,001J=1\mathrm{mJ}$. Les parties verticales ont leur centre de gravité à une hauteur de $h_1=h_3=5\mathrm{cm}$, donc leur énergie potentielle est de $E_1=E_3=m_{0}g{h}_1=m_{0}g{h}_3=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,05m=0,0005J=0,5\mathrm{mJ}$.

Par conséquent, l’énergie potentielle maximale du ver sera de $E=E_1+E_2+E_3=0,5\mathrm{mJ}+1\mathrm{mJ}+0,5\mathrm{mJ}=2\mathrm{mJ}$, ce qui est également le travail que le ver doit effectuer.

Résultat:

$1050$

Nous pouvons diviser le problème en parties plus gérables. Tout d’abord, combien d’essais nous faut-il pour arriver à ABA ? Puisque l’alphabet anglais compte $26$ lettres, il faudra $26$ itérations pour changer la dernière lettre. Et BAA ? Eh bien, pour chaque $26$ itérations de la dernière lettre, la deuxième lettre augmentera de $1$, donc pour passer de AAA à BAA, nous avons besoin de $26\cdot 26=676$ essais. Maintenant, pour passer de BAA à BOA, il nous faut $26\cdot 14=364$ essais, car O est la $15$-ème lettre de l’alphabet et nous devons essayer toutes les $14$ lettres qui la précèdent. Enfin, J est la $10$-ème lettre, donc nous avons besoin de $10$ essais supplémentaires pour passer de BOA à BOJ. Tout cela fait un total de $676+364+10=1050$ essais.

Résultat:

$125$

Le mécanisme reste au repos uniquement si le moment de force agissant sur chacun des leviers s’annule. Nous devons donc examiner les moments de force agissant sur les leviers. Pour cela, commencez par comprendre les cordes. Il y aura une tension dans chaque corde, de sorte que la corde agira sur les deux leviers avec une force de même magnitude que cette tension. Par exemple, la corde reliant le levier du milieu et le levier de droite agira avec la même force sur le levier du milieu (vers la droite) que sur le levier de droite (vers la gauche). De plus, notez que ces forces agissent également à la même hauteur, elles agissent donc à la même distance des axes de rotation des leviers. Par conséquent, chaque corde agit également sur les deux leviers avec un moment de force de même magnitude.

Cela signifie essentiellement que nous pouvons oublier le levier du milieu. En effet, la force agissant sur le levier de droite provoque un certain moment de force de magnitude $M$ sur le levier de droite. Cela doit être compensé par le moment de force de la corde attachée au levier de droite. Puisque les cordes portent le moment de force, la magnitude du moment de force avec lequel la corde de droite agit sur le levier du milieu doit être à nouveau $M$. De même, le moment de force sur le levier de gauche aura une magnitude de $M$.

Par conséquent, pour que le mécanisme reste au repos, les deux forces pertinentes doivent avoir un moment de force de même magnitude. Cela nous mène à l’équation :

Ainsi, Patrick doit tirer avec une force d’intensité $125N$.

Résultat:

$2,15$

Soit les longueurs et les noms des sommets comme dans la figure suivante :

Considérons les triangles rectangles $\mathit{ABP}$ et $\mathit{ACP}$. Par le théorème de Pythagore, on obtient :

Si nous exprimons $h^2$ des deux égalités et les comparons, nous obtenons :

Maintenant, nous pouvons appliquer la formule $a^2-b^2=(a-b)(a+b)$ des deux côtés pour obtenir :

Mais nous savons que $y+x=20\mathrm{cm}$. Par conséquent, la différence des longueurs $y-x$, que nous devons trouver, est :

Résultat:

$75$

Désignons par $m$ la masse d’un chariot de montagnes russes, $r=30m$ le rayon de la boucle et $v$ la vitesse du chariot au point le plus élevé de la boucle.

D’après la première partie de l’énoncé du problème, nous savons qu’au point le plus élevé de la boucle, il doit y avoir une certaine force centripète $F_c=\frac{m{v}^2}{r}$. Il y a deux forces qui peuvent agir sur le chariot dans cette direction - la force gravitationnelle $F_g=\mathit{mg}$ et une force de la boucle. Mais nous voulons que la force centripète soit aussi faible que possible (plus la force centripète est grande, plus le chariot doit avoir de vitesse et plus l’énergie qu’il a au départ doit être élevée). Comme nous ne pouvons pas nous débarrasser de la force gravitationnelle, dans le cas minimal, nous aurons $F_c=F_g$. De cela, nous obtenons :

Maintenant, regardons les énergies. Au départ, le chariot n’a que de l’énergie potentielle $E_1=\mathit{mgh}$. Cependant, au sommet de la boucle, le chariot a à la fois de l’énergie potentielle et cinétique. Il se trouve à une hauteur $2r$ et a une vitesse $v$, donc son énergie est $E_2=\mathit{mg}(2r)+\frac{1}{2}m{v}^2$. L’énergie doit se conserver, donc $E_1=E_2$. En combinant cela avec l’équation pour $v^2$, nous obtenons :

Par conséquent, le chariot doit descendre d’une hauteur de $h=\frac{5}{2}r=\frac{5}{2}\cdot 30m=75m$.

Résultat:

$23$

La solution se divise naturellement en deux parties. Dans la première, nous montrons que $23$ matchs pourraient avoir été joués. Dans la deuxième, nous prouvons que si $24$ matchs avaient été joué, il existerait un tel groupe. Cela signifie que la réponse est de $23$.

Première partie : Numérotez les joueurs avec des numéros de $1$ à $24$. Les matchs se déroulent entre le joueur $1$ et le joueur $2$, le joueur $2$ et le joueur $3$, et ainsi de suite jusqu’au joueur $23$ et le joueur $24$. Choisissez n’importe quel groupe de joueurs. Dans ce groupe, il y a toujours un joueur avec le plus petit numéro, appelons-le $P$. Au sein de ce groupe, ce joueur ne peut jouer qu’un match avec $P+1$, car le joueur $P-1$ ne peut pas être dans le groupe (il aurait un numéro plus bas). Par conséquent, le joueur avec le numéro $P$ n’a pas joué contre au moins $2$ personnes de ce groupe. Cela vaut pour n’importe quel groupe, il n’y a donc pas de groupe de joueurs satisfaisant la condition de l’énoncé du problème. Par conséquent, $23$ matchs pourraient avoir été joués.

Deuxième partie : Nous devons prouver que si $24$ matchs étaient joués, il existe toujours un groupe avec la propriété de l’énoncé du problème. Si une paire de joueurs avait joué au moins deux matchs l’un contre l’autre, ils formeraient un groupe valide. Nous pouvons donc supposer qu’il n’y a pas de telle paire.

Maintenant, supposons que chaque joueur ait joué au moins $2$ matchs. Sélectionnez les joueurs comme suit : commencez par n’importe quel joueur, appelez-le $P_0$. Il a joué avec quelqu’un, disons $P_1$. Le joueur $P_1$ a joué avec au moins deux joueurs, il y a donc un joueur $P_2$ différent de $P_0$, avec lequel $P_1$ a joué. De la même manière, nous trouvons un joueur $P_3$ différent de $P_1$, tel que $P_2$ a joué avec $P_1$ et $P_3$. De cette façon, nous continuons à prendre des joueurs. À un moment donné, nous obtenons un joueur qui a déjà été nommé. À ce stade, nous avons des joueurs $P_k$, $P_{k+1}$, ..., $P_n$ ayant la propriété que le joueur $P_i$ a joué avec les joueurs $P_{i-1}$ et $P_{i+1}$, et les joueurs $P_k$ et $P_n$ ont joué l’un contre l’autre. En d’autres termes, nous pouvons les disposer en cercle dans l’ordre donné de telle sorte que chacun d’entre eux ait joué avec ses deux voisins. Cela prouve que ce groupe a la propriété requise. Donc, si tout le monde avait joué au moins $2$ matchs, nous avons terminé.

Il reste à vérifier ce qui se passe si un joueur a joué moins de $2$ matchs. Dans ce cas, nous oublions ce joueur. Après avoir fait cela, il nous restera moins de joueurs. Cependant, le nombre de matchs restera toujours au moins égal au nombre de joueurs. Après avoir oublié ce joueur, il y a deux possibilités : soit tout les joueurs restants ont joué au moins $2$ matchs, soit il y a à nouveau quelqu’un qui a joué moins de $2$ matchs. Dans le premier cas, l’argument précédent montre qu’il existe un groupe satisfaisant la condition de l’énoncé du problème. Sinon, nous avons un autre joueur à oublier. De cette manière, nous continuons. Si nous pouvons continuer à diminuer le nombre de joueurs, nous finirons par n’avoir que $3$ joueurs, qui ont joué au moins $3$ matchs entre eux. Ceci n’est possible que s’ils ont joué les uns contre les autres, formant ainsi le groupe que nous essayons de trouver.

Cela prouve que si $24$ matchs avaient été joués, un tel groupe existerait. En combinant tout cela, nous concluons que le nombre maximum de matchs joués est de $23$.

Résultat:

$25$

Tout d’abord, nous devons découvrir la règle de divisibilité par $125$. Le critère est que le nombre formé par les trois derniers chiffres doit être divisible par $125$ (ceci est similaire aux critères de divisibilité par $2$, $4$, $8$, $16$ …, mais aussi avec $5$, $25$, $125$ …). Pourquoi ? Écrivez un nombre comme $1000A+B$, où $B<1000$. $B$ est donc le nombre formé par les trois derniers chiffres. Remarquez que $1000$ est divisible par $125$ car $1000=8\cdot 125$. Par conséquent, pour que le nombre $1000A+B$ soit divisible par $125$, il faut que $B$ soit divisible par $125$. Cela prouve le critère.

Maintenant, voyons quelles en sont les conséquences. Les seuls nombres d’au plus $3$ chiffres divisibles par $125$ sont $0$, $125$, $250$, $375$, $500$, $625$, $750$ et $875$. Aucun d’entre eux ne commence par le chiffre $4$. Par conséquent, nous en concluons que les multiples de $125$ ne peuvent pas avoir le chiffre $4$ comme chiffre des centaines.

Enfin, revenons à notre problème initial. Nous savons que le chiffre des centaines est $4$, donc le résultat de Lucie ne peut pas être un multiple de $125$. Si elle n’avait omis aucun nombre, le produit final serait divisible par $5\cdot 15\cdot 25$. Par conséquent, la décomposition en facteurs premiers du produit contiendrait le nombre $5$ quatre fois. Nous devons donc supprimer le nombre $5$ au moins deux fois. Cela n’est possible qu’en enlevant le nombre $25$. Cela signifie que Lucie a omis le nombre $25$.

Résultat:

$28$

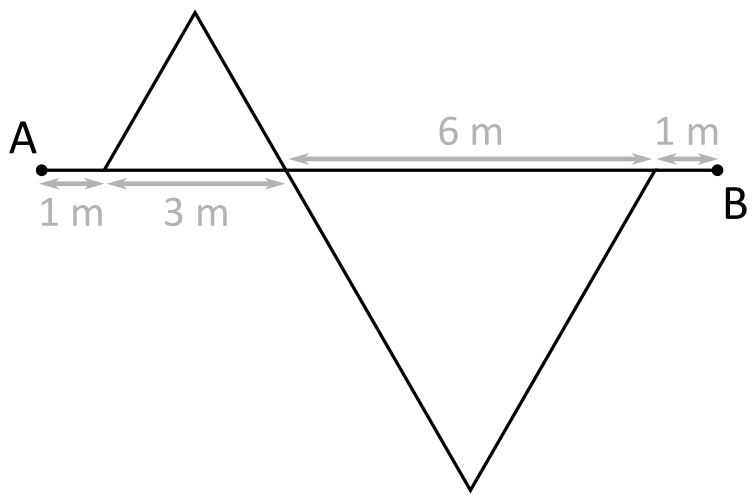
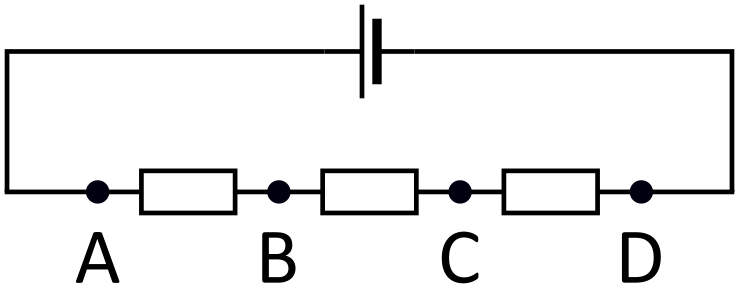
Une tension entre deux points décrit la magnitude de la différence de potentiels entre ces deux points. Le potentiel décrit uniquement l’énergie potentielle (électrique) d’une particule de charge $1C$. À chacun des points $A$, $B$, $C$ et $D$, cette particule aurait une certaine énergie potentielle, et nous pouvons attribuer ce nombre à chacun de ces points. Ensuite, les tensions ne font que décrire les différences entre ces nombres.

Nous pouvons donc reformuler le problème en un problème mathématique consistant à attribuer quatre nombres à $A$, $B$, $C$ et $D$ (maintenant, ces lettres n’ont rien à voir avec les points du problème de physique d’origine), de telle sorte que leurs différences soient de $7$, $8$, $10$, $15$, $18$ et une inconnue. Remarquez une propriété intéressante : prenons trois des nombres, disons $X$, $Y$ et $Z$, et supposons qu’ils soient ordonnés de telle sorte que $X>Y>Z$. Alors, la différence $X-Z$ est la somme des différences $X-Y$ et $Y-Z$ (clairement $(X-Y)+(Y-Z)=X-Z$). Ainsi, si nous prenons n’importe quel triplet de nombres, alors les différences entre eux auront la propriété que l’une d’entre elles sera la somme des deux autres.

Nous pouvons maintenant revenir au problème. Disons que la différence inconnue est la différence entre $C$ et $D$. Prenez les nombres $A$, $B$ et $C$. Les trois différences entre eux font partie de celles connues. Comme l’une d’entre elles doit être la somme des deux autres, nous n’avons que deux possibilités : $7+8=15$ ou $8+10=18$. La même chose doit s’appliquer au triplet $A$, $B$ et $D$, de sorte que l’une de ces paires de triplets contienne les différences $7$, $8$ et $15$ et l’autre les différences $8$, $10$ et $18$. Disons que le triplet $A$, $B$ et $C$ a (dans un certain ordre) les différences $7$, $8$ et $15$. Les triplets $A$, $B$ et $C$ et $A$, $B$ et $D$ ne coïncident que dans la différence entre $A$ et $B$, alors cette différence doit être de $8$ (c’est la seule différence dans laquelle les triplets $7$, $8$, $15$ et $8$, $10$, $18$ coïncident).

Jusqu’à présent, les nombres $A$ et $B$ peuvent être échangés, nous pouvons donc choisir la différence entre $A$ et $C$ pour être de $15$ et la différence entre $B$ et $C$ pour être de $7$. Dans le triplet $A$, $B$ et $C$, nous savons que les nombres $A$ et $C$ sont soit les plus grands, soit les plus petits. Choisissons-les de telle sorte que $A$ soit le plus grand. Maintenant, nous avons deux possibilités pour les différences entre $D$ et les nombres $A$ et $B$.

Cas 1 : Si la différence entre $A$ et $D$ est de $18$. Cela signifie que dans le triplet $A$, $B$ et $D$, l’un des nombres $A$ et $D$ est le plus grand et l’autre le plus petit. Mais dans le triplet $A$, $B$ et $C$, nous avons choisi $A$ comme le plus grand, il est donc plus grand que $B$. Par conséquent, dans le triplet $A$, $B$, $D$, nous savons que $A$ doit être le plus grand. Cela signifie que $A$ est supérieur de $15$ à $C$ et de $18$ à $D$. Par conséquent, la différence entre $C$ et $D$ est $(A-15)-(A-18)=3$. C’est la première solution.

Cas 2 : Si la différence entre $A$ et $D$ est de $10$. Cela signifie que dans le triplet $A$, $B$ et $D$, l’un des nombres $B$ et $D$ est le plus grand et l’autre le plus petit. De manière similaire au cas précédent, nous savons que $A$ est supérieur à $B$, donc $B$ doit être le plus petit. Par conséquent, nous savons que $C$ est inférieur de $7$ à $B$ et que $D$ est supérieur de $18$ à $B$. Cela signifie que la différence entre $C$ et $D$ est $(B+18)-(B-7)=25$, ce qui est la deuxième solution.

Pour résumer, nous avons découvert que la différence inconnue ne peut être que $3$ ou $25$. Dans le problème d’origine, cela signifie que la tension inconnue ne peut être que $3V$ ou $25V$. La somme de ces deux tensions inconnues possibles est donc $3V+25V=28V$.

Résultat:

$91$

Avant de commencer, examinons l’aire d’un triangle équilatéral de côté $x$. En utilisant le théorème de Pythagore, il est facile de calculer que la hauteur de ce triangle est $\frac{\sqrt{3}}{2}x$. Ainsi, l’aire d’un triangle équilatéral est $\frac{x\cdot \frac{\sqrt{3}}{2}x}{2}=\frac{\sqrt{3}}{4}{x}^2$.

Revenons maintenant au problème original. Nommons les sommets de l’hexagone $A$, $B$, $C$, $D$, $E$, $F$, de telle sorte que $\mathit{AB}=10m$, $\mathit{BC}=12m$, $\mathit{CD}=4m$, $\mathit{DE}=8m$, $\mathit{EF}=14m$, $\mathit{FA}=2m$. Faisons interagir les lignes $\mathit{AB}$, $\mathit{CD}$ et $\mathit{EF}$ pour obtenir le triangle $\mathit{KLM}$ comme dans la figure :

Puisque les angles intérieurs dans l’hexagone $\mathit{ABCDEF}$ étaient de $120^{\circ }$, nous obtenons que les triangles $\mathit{KAF}$, $\mathit{LBC}$ et $\mathit{MDE}$ sont équilatéraux. Cela donne immédiatement que le triangle $\mathit{KLM}$ est équilatéral de côté $24m$.

L’aire de l’hexagone $\mathit{ABCDEF}$ est donnée comme la différence entre l’aire du triangle équilatéral $\mathit{KLM}$ et la somme des aires des triangles équilatéraux $\mathit{KAB}$, $\mathit{LBC}$ et $\mathit{MDE}$. Par conséquent, l’aire de l’hexagone $\mathit{ABCDEF}$ est :

Cela signifie que la valeur de $a$ est $91$.

Résultat:

$75$

Désignons les surfaces du premier piston $S_1$, du deuxième piston $S_2$ et du troisième piston $S_3$. Les conditions données indiquent que $S_1=S_2+S_3$.

De plus, soit $m$ la masse du hamster et $\mathrm{\Delta }{h}_1=15\mathrm{mm}$ la hauteur de descente du premier piston lorsque le hamster y est placé. En même temps, le deuxième piston monte de $\mathrm{\Delta }{h}_2$ et le troisième piston monte de $\mathrm{\Delta }{h}_3$. Après avoir placé le hamster sur le premier piston, deux choses doivent se produire. Premièrement, l’eau provenant du premier piston doit se diviser entre les autres pistons. Cela donne la condition $S_1\mathrm{\Delta }{h}_1=S_2\mathrm{\Delta }{h}_2+S_3\mathrm{\Delta }{h}_3$. D’autre part, la pression des trois pistons doit être la même. Si $p$ était la pression initiale dans le système et $\rho$ la densité de l’eau, cela donne : $p+\frac{\mathit{mg}}{S_1}-\mathrm{\Delta }{h}_1\mathit{\rho g}=p+\mathrm{\Delta }{h}_2\mathit{\rho g}=p+\mathrm{\Delta }{h}_3\mathit{\rho g}$. Nous pouvons soustraire $p$ et diviser par $g$ pour obtenir $\frac{m}{S_1}-\mathrm{\Delta }{h}_1\rho =\mathrm{\Delta }{h}_2\rho =\mathrm{\Delta }{h}_3\rho$. La deuxième partie de cette équation donne que $\mathrm{\Delta }{h}_2=\mathrm{\Delta }{h}_3$. En utilisant cette équation dans les équations précédentes, nous obtenons :

Ou sous une autre forme :

En comparant ces deux équations, nous obtenons :

Nous redéfinissons maintenant $\mathrm{\Delta }{h}_2$ pour désigner la hauteur de descente du deuxième piston lorsque le hamster y est placé et de même $\mathrm{\Delta }{h}_3$ pour le troisième piston. De la même manière que ci-dessus, nous trouvons que :

Si nous divisons les deux premières équations et utilisons $S_1=S_2+S_3$, nous obtenons :

À partir de $S_1=S_2+S_3$, nous obtenons que $S_3=S_1-S_2=S_1-\frac{2}{3}{S}_1=\frac{1}{3}{S}_1$. En divisant les deux premières équations, nous obtenons :

Donc, si on met le hamster sur le troisième piston, il descendra de $75\mathrm{mm}$.

Résultat:

$999$

Le nombre préféré de Matthias ne peut pas être un nombre formé d’un seul chiffre. Si c’était un chiffre $a$, la condition signifierait que $a^2=a$, ce qui n’est vrai que pour $a=0$ ou $a=1$, mais le nombre doit être supérieur à $1$.

Le nombre préféré de Matthias ne peut pas non plus être un nombre à deux chiffres. En effet, si le nombre est $10a+b$, nous aurions ${(a+b)}^2=\mathit{ab}$ ou $a^2+\mathit{ab}+b^2=0$. Mais comme $a$ et $b$ sont des nombres non négatifs et que $a$ est positif, nous avons toujours $a^2+\mathit{ab}+b^2>0$, donc $a^2+\mathit{ab}+b^2=0$ ne peut jamais être vérifié.

Ensuite, nous montrons que $999$ est le seul nombre à trois chiffres ayant les propriétés données. On trouve facilement qu’il satisfait ces propriétés $({(9+9+9)}^2=27^2=3^6=9^3=9\cdot 9\cdot 9)$. Il nous reste à démontrer que c’est le seul nombre à trois chiffres qui les satisfait.

Soit $100a+10b+c$ le nombre ayant les propriétés données, ce qui signifie que ${(a+b+c)}^2=\mathit{abc}$. $a$, $b$ et $c$ sont des chiffres, donc nous devons avoir $0\le a,b,c\le 9$. De toute évidence, si l’un des chiffres est $0$, la relation ${(a+b+c)}^2=\mathit{abc}$ force tous les autres chiffres à être $0$. Nous pouvons donc supposer que $1\le a,b,c$. De plus, la relation ${(a+b+c)}^2=\mathit{abc}$ est symétrique par rapport aux valeurs de $a$, $b$ et $c$, nous pouvons donc supposer que $a\le b\le c$ (cette condition produira le plus petit nombre à trois chiffres à partir de n’importe quel triplet valide). Ainsi, nous supposons que :

Examinons de plus près ${(a+b+c)}^2=\mathit{abc}$. Il peut être écrit comme $a^2+b^2+c^2+2\mathit{ab}+2\mathit{ac}+2\mathit{bc}=\mathit{abc}$. En utilisant $c\le 9$, nous savons que $\mathit{abc}\le 9\mathit{ab}$. D’un autre côté, en utilisant $a\le b\le c$, nous savons que :

De plus, ${(a-b)}^2\ge 0$, donc $a^2+b^2\ge 2\mathit{ab}$. En combinant ces inégalités, nous obtenons :

Puisque le côté gauche et le côté droit de cette inégalité sont les mêmes, toutes les inégalités utilisées doivent être vérifiées.

• Dans l’inégalité $\mathit{abc}\le 9\mathit{ab}$, il y a égalité si et seulement si $c=9$.
• Dans l’inégalité $\mathit{ac}\ge \mathit{ab}$, il y a égalité si et seulement si $b=c$.
• Dans l’inégalité $\mathit{bc}\ge \mathit{ab}$, il y a égalité si et seulement si $a=c$.

En combinant ces trois observations, nous en concluons que le seul cas possible est $a=b=c=9$. Comme nous l’avons déjà vérifié, c’est effectivement une solution. Donc, le nombre $999$ est le seul nombre à trois chiffres satisfaisant les conditions données. Par conséquent, c’est le plus petit nombre supérieur à $1$ ayant les conditions données, ce qui signifie que $999$ est le nombre préféré de Matthias.