Probleemopgaven

Antwoord:

In 2012 was de appelboom hoog. Gedurende tien jaar werd de appelboom elk jaar hoger. Dus, de hoogte van de boom in 2022 is .

Antwoord:

Om het antwoord te vinden is het genoeg om het aantal zijden te tellen dat Anna heeft gelopen. Uit de figuur blijkt dat Anna zijden heeft gelopen, wat overeenkomt met een afstand van .

Antwoord:

De gemiddelde snelheid van George is gelijk aan de afgelegde afstand gedeeld door de tijd die nodig was om de afstand af te leggen. Uit de grafiek blijkt dat George een afstand heeft afgelegd van gedurende , wat betekend dat zijn gemiddelde snelheid was.

Antwoord:

De letter N moet als eerste worden verzameld. Als we eerst de N meenemen die twee hokes rechts van het startvak is, moet de Á daarna verzameld worden. Dat kan door een hokje naar rechts en een hokje naar beneden te bewegen. Vervolgens moet de B verzameld worden. Vanaf de huidige positie is het onmogelijk om een B te bereiken door alleen maar te bewegen naar rechts of beneden. Dat betekent dus dat de letter N onder het startvak de eerste letter moet zijn.

Als we van daaruit naar de Á willen die drie hokjes naar rechts is, lopen we tegen hetzelfde probleem aan omtrent de letter B als in de vorige alinea. Daarom nemen we de Á onder de N mee als tweede letter.

Als we van daaruit doorgaan naar de B in de linkeronderhoek, kunnen we de J alleen maar bereiken door naar rechts te gaan. Deze route is mogelijk, omdat we tussen de B en J nog de letter O bereiken. Dit is dus het eerste mogelijke pad

Als we doorgaan vanaf de B in de derde rij en de derde kolom, zijn er twee manieren waarop we een O kunnen bereiken. De O in de onderste rij geeft een enkele optie om J te bereiken. Dat is dus route 2. Vanaf de O die direct naast de B ligt zijn er drie manieren om J te bereiken. Dat zijn routes 3, 4 en 5.

Alle mogelijke routes zijn weergegeven in de figuur hieronder:

Er zijn dus vijf mogelijke manieren waarop Daniel het muntje kan bewegen.

Antwoord:

De lichtstraal die in de figuur is afgebeeld zal de linkermuur raken na 1 meter extra omhoog afgelegd te hebben. De straal raakt de linkermuur dus twee meter boven het beginpunt. Dan zal de straal zo gereflecteerd worden dat hij de rechtermuur nog een extra meter hoger raakt. Dat is dus exact waar de ballon zich bevindt. Het traject van de straal staat afgebeeld in de figuur hieronder:

De straal wordt dus twee keer gereflecteerd.

Antwoord:

Laura kan kilometer per uur fietsen. Omdat een ¨naarschool¨ 3 kilometer is, is dat naarschool per uur. Een ¨schoolles¨ is slechts van een uur. Als Laura naarschool per uur kan rijden, dan rijdt ze per driekwartier (ofwel per een ¨schoolles¨) ¨naarschool¨. Dus Laura kan 6 naarschool per schoolles fietsen.

Antwoord:

Het enige getal dat start met is . is echter geen positief getal, dus kan het geen afnemend getal zijn. Als het eerste cijfer is, kan het gevolgd worden door een of door niks. en zijn dus afnemende getallen. Als het eerste cijfer is, kan het gevolgd worden door , of niks. Dat geeft de extra oplossingen , , en . Er zijn dus afnemende getallen.

Antwoord:

Matthijs rendde met een snelheid van . Hij deed dus over de race.

Mark fietste met een snelheid van , dus had hij nodig. Omdat Mark Matthijs een voorsprong van minuten heeft gegeven, komt hij nadat Matthijs startte binnen.

Mark finishte dus voor Matthijs.

Antwoord:

Als de stoelnummers een van de getallen , , , , of bevatten, moet het getal of het omgedraaide getal een veelvoud zijn van of . De getallen waar we naar op zoek zijn mogen dus geen enkele van deze cijfers bevatten. De getallen mogen dus bestaan uit de cijfers , , en . Er zijn slechts tweecijferige getallen die aan deze voorwaarde voldoen, namelijk:

Van deze getallen zijn de volgende geen priemgetallen: , , , , en . Deze getallen vallen dus af. Ook het getal valt af, omdat geen priemgetal is. De volgende getallen blijven over:

Matthias heeft maximaal tickets kunnen bestellen.

Antwoord:

De afstand die het kind overbrugt kan berekend worden met de stelling van Pythagoras. De afstand is dus . Zoals genoemd duurt het om van de glijbaan af te gaan. Dus is de gemiddelde snelheid .

Antwoord:

Een rechthoek kan alleen in twee rechthoeken verdeeld worden door een lijnsegment dat parallel is aan twee zijden van de grote rechthoek. In dit geval is de lengte van het segment gelijk aan de lengte van de zijde waarmee het parallel loopt.

De omtrek van de grote rechthoek is , met een zijde die lang is. De andere zijde moet dan een lengte hebben zodat holds. Uit deze vergelijking volgt dat .

Het idee van deze oplossing is dat de lengte van de zijde gelijk moet zijn aan de lengte van het pad bij de andere manier van de rechthoek verdelen. Dus moet de lengte van het pad zijn.

Antwoord:

Hierzo geldt de wet van actie en reactie. Deze wet stelt dat wanneer een object een kracht uitoefent op een object , dat object een even grote kracht op uitoefent, maar in tegengestelde richting. De aarde oefent dus een kracht uit op Max van . Max moet daarom de aarde aantrekken met een even grote gravitatiekracht, dus met een kracht van .

Antwoord:

Stel de afstand die Sabine heeft afgelegd. Als ze niet zou stoppen, zou het uur duren om de afstand af te leggen. Echter, omdat ze een pauze nam van minuten, deed ze over de afstand. Door deze pauze was Sabine´s gemiddelde snelheid gelijk aan . Dat geeft de volgende vergelijking: Sabine heeft dus een afstand afgelegd van .

Antwoord:

De gok die ernaast zat met moet ofwel de grootste of kleinste zijn van de gegeven gokken. Als het de kleinste was, moet het aantal juist opgeloste opgaven of zijn. De eerste optie kan niet, omdat de rest er dan naast zit met meer dan opgaven. Voor de tweede optie verschillen de rest van de gokken met , and , wat niet overeenkomt met de gegeven getallen.

Het teamlid dat gokte moet er dus naast hebben gezeten met opgaven. Volgens een analoge redenering kan het aantal opgeloste opgaven niet , maar moet het zijn. In dit geval verschillen de gokken met de werkelijkheid met , en opgaven, wat overeenkomt met de gegeven aantallen.

Vandaar dat het team opgaven correct heeft opgelost.

Antwoord:

Laten we kijken wat er gebeurt als iemand zegt dat een ander (niet) een spion is. Annemijn zegt bijvoorbeeld dat David een spion is. Als Annemijn de waarheid vertelt (Dus als ze niet een spion is), dan is David een spion. Als Annemijn liegt (Dus als ze een spion is), dan is David niet een spion. Dit betekent dat Annemijn en David elkaars tegengestelde zijn - een van hen is een spion, de ander niet. Laten we nu kijken naar Bob’s uitspraak. Als Bob de waarheid vertelt (Dus als hij niet een spion is), dan is Casper ook geen spion. Maar als Bob liegt (en dus een spion is), dan is Casper ook een spion. Dit betekent dat Bob en Casper aan dezelfde kant zitten - ze zijn of geen van beiden een spion, of beiden een spion. Op dezelfde manier zitten David en Erik aan dezelfde kant. Als Annemijn dus een spion was, dan zijn of Bob en Casper, of David en Erik ook spionnen. In dat geval zouden we dus minstens drie spionnen hebben, wat niet het geval is. Annemijn is dus in elk geval geen spion, en ze zegt dat David een spion is, dus is David een spion. Maar als hij een spion was, dan is Erik ook een spion aangezien ze aan dezelfde kant zaten. Dus Erik is ook een spion. De overige twee, Bob en Casper, zijn geen spionnen.

De spionnen zijn dus David en Erik, van wie de som van de getallen is.

Antwoord:

Noem de grootte van Marks bestand . Als Mark het bestand uploadt zonder te comprimeren, zal het duren. Als Mark besluit het bestand te comprimeren, zal dat duren. Vanaf dat moment is de groote van het bestand . Na seconden zal Mark starten met het uploaden van het bestand en het uploaden zal duren. Dus zal het hele proces met compressie duren. Het probleem zegt dat deze tijd gelijk is aan de uploadtijd zonder compressie. Dat lijdt tot de volgende vergelijking, die we als volgt kunnen oplossen: Dus hebben we de grootte van Marks bestand als uitgerekend.

Antwoord:

We merken op dat de omtrek van de tuin gelijk is aan de som van de omtrekken van de bloembedden met omtrekken , en het bloembed met het vraagteken erin. dit is omdat sommige zijdes van deze drie bloembedden naar de zijdes van de tuin verplaatst kunnen worden om de omtrek van de hele tuin te maken:

Hieruit volgt dat de omtrek van het bloembed met het vraagteken is.

Antwoord:

Hoe groter de afstand waarop Adriaan remt, hoe kleiner de kracht die hij nodig heeft. Neem dus aan dat de auto op de afstand remt. om de auto te stoppen, moet de auto arbeid leveren om de remkracht te evenaren, wat ten koste gaat van de energie van de auto, in dit geval de kinetische energie.

De kinetische energie van de auto met massa en snelheid is . Er moet dezelfde hoeveelheid arbeid geleverd worden door de kracht met grootte , waarmee de auto de evengrote remkracht overkomt. Deze kracht levert op de afstand arbeid . Dat levert de volgende vergelijking Dus moet de remkracht op de auto minstens de volgende grootte hebben:

Antwoord:

Het bedrag kan op geen enkele manier betaald worden - we kunnen of munt met waarde gebruiken, anders zouden we boven uitkomen. In beide gevallen kunnen we de rest niet betalen met slechts munten van waarde . We kunnen echter elke prijs hoger dan betalen. Begin met de prijzen (), () en (). Als we deze drie prijzen kunnen betalen, kunnen we ook elke hogere prijs betalen - we hebben alleen maar genoeg munten van waarde nodig.

Dus is het grootste bedrag dat Merel niet zou kunnen betalen zonder geld terug te krijgen .

Antwoord:

De hele situatie is symmetrisch rond de lijn die de ballen verbindt. dat zal zo blijven, ook na de botsing, als de ballen een grotere massa vormen. Als deze massa naar links of naar rechts zou bewegen, zou de symmetrie verbroken worden. daarom moet de gevormde massa stilstaan.

Bij de botsing zullen de ballen hun kinetische energie verliezen, die, zoals aangenomen in de opgave, omgezet wordt in warmte, die de gevormde massa verhit. beide ballen (met massa en snelheid ) hebben een kinetische energie . samen hebben ze een kinetische energie van . deze energie wordt aan de gevormde massa gegeven in de form van warmte. Die heeft een massa van (het bevat beide ballen met een massa van ), een specifieke warmtecapaciteit van en zijn temperatuur verandert met . daarom geldt het volgende: Als de temperatuur van de ballen voor de botsing was, dan is de temperatuur vna de gevormde massa na de botsing:

Antwoord:

Om de wip uit te balanceren, moeten de koppels op beide zijdes van de wip gelijk zijn. Danielle, met een massa van , zit op een afstand van het draaipunt. Op Danielle werkt een zwaartekracht . Danielle levert een even grote kracht uit op de wip, en deze kracht werkt met koppel: De kubussen aan de andere kant moeten met hetzelfde moment werken. neem aan dat er kubussen zijn. De opgave geeft ons dat elke kubus een massa van en een breedte van heeft. Dan hebben ze samen een massa van en vormen ze een rechthoek met lengte . Het zwaartepunt hiervan ligt op een afstand van van het draaipunt, dus dit is de afstand waarop de zwaartekracht van de rechthoek op de wip werkt. Het koppel van deze rechthoek is dan: De koppels en moeten gelijk zijn. de bovenstaande twee vergelijkingen vergelijken geeft: Dus is het aantal kubussen die Nina op de wip moet leggen:

Antwoord:

Kijk naar de getallen die in de positie van de enkelvouden staan. De cijfers , en kunnen daar niet staan omdat het getal dan deelbaar is door , waardoor het niet priem is. Om eenzelfde reden kan er ook niet staan, omdat het getal dan deelbaar is door . Daarom zullen de getallen , , en in de positie van de tienvouden staan, en zullen de andere getallen (, , en ) in de enkelvouden staan. Dus is de enige, en dus ook de maximale som van vier priemgetallen .

De kaarten kunnen echt gebruikt worden om -cijferige priemgetallen te maken. Bijvoorbeeld zo: , , en .

Antwoord:

Lijnen in een vlak die niet snijden, lopen parallel aan elkaar. Dus proberen we het aantal paren parallelle lijnen te vinden bepaald door de aangegeven punten.

Noem de aangegeven punten , , , , , en . We beginnen met alle lijnen vinden die parallel zijn aan de lijn . Dat zijn de lijnen en . Dat is omdat de regelmatige zevenhoek symmetrisch is in de middelloodlijn van , en dus paargewijs parallel is. Zo krijgen we paren parallelle lijnen.

Door hetzelfde idee te herhalen voor de lijnen , , , , en , krijgen we paren parallelle lijnen in elk van de gevallen.

Elke lijn bepaald door de punten tot maken we parallel aan een van de lijnen , , , , , and (deze lijnen snijden elkaar met hun paren). dus vinden we zo alle paren parallelle lijnen.

In totaal kan Tessa dus de paren lijnen op verschillende manieren tekenen.

Antwoord:

De hoogte-energie van de bal als hij gegooid wordt is , waarin de massa is, de hoogte vanwaar hij gegooid wordt is en de valversnelling is. Als we zeggen , dan is de kinetische energie van de bal, als hij gegooid wordt, . tijdens de beweging blijft de totale hoeveelheid energie van de bal gelijk. Dus is de som op elk moment gelijk. Dus is die som ook gelijk net voor de bal de grond raakt. Op dat moment heeft de bal geen hoogte, dus is de hoogte-energie nul. dus is de totale energie op dat moment de kinetische energie. Als we zeggen dat de kinetische energie van de bal is vlak voor de landing, krijgen we de volgende vergelijking: Dus is de snelheid van de bal vlak voor de landing:

Antwoord:

Het enige een-cijferige getal dat gelijk is aan keer de som van de cijfers, is het getal . Zelfs als een natuurlijk getal is (in sommige delen van de wiskunde is een natuurlijk getal, in anderen niet), zou het de som niet aanpassen.

Als Jonas een werkend tweecijferig getal vindt, zouden we het kunnen schrijven als , waar en de cijfers zijn. De som keer van dit getal is echter en . Daarom zal dertien keer de som van de cijfers van een twee-cijferig getal nooit gelijk zijn aan het getal zelf.

Laten we nu kijken naar de driecijferige getallen, waarvan elke geschreven kan worden in de vorm . Omdat het getal uit drie cijfers bestaat, weten we . De som van de cijfers leidt tot de volgende relatie: Als hebben we drie opties voor de cijfers en . De waardes van zijn daarin , en , die overeenkomen met de getallen , en . we hebben geen andere opties voor , aangezien , en voor hebben we , terwijl we tegelijkertijd moeten hebben. In andere opties voor zijn er dus geen en die aan voldoen. Dus we hebben alle driecijferige getallen gehad.

Een viercijferig getal heeft een som van de cijfers van maximaal , dus het -voud van de som van de cijfers zal zeker minder zijn dan (We kunnen natuurlijk ook uitreken, maar deze manier laat ons al tot de volgende conclusie komen). Daarom zal het -voud van de som van de cijfers zeker kleiner zijn dan het getal zelf. Daarom zal Jonas zeker geen viercijferig getal gevonden hebben. Om eenzelfde reden zal Jonas ook geen getallen gevonden hebben met meer cijfers.

Alles samengenomen zal Jonas dus getallen met een som van gevonden hebben.

Antwoord:

Beide diagonalen van een vierkant bord hebben dezelfde lengte en snijden elkaar loodrecht. we weten dat de lengte van een van de diagonalen is. elk van de diagonalen verdeelt het vierkant in twee driehoeken, waarvan de hoogte de helft van de andere diagonaal is. Zo’n driehoek heeft oppervlakte . Het hele bord bestaat uit twee zulke driehoeken, dus de oppervlakte is = 72 dm².

Het gele deel is van het hele bord, dus is de oppervlakte ervan . De zijkant is daarom lang.

Antwoord:

Noem de lengte van de loopband . Van het geval waarin Julia alleen op de loopband staat, kunnen we de snelheid vinden. Het kost Julia om bij de andere kant van de band te komen, dus de snelheid van de band is . Op dezelfde wijze kunnen we van het geval dat Julia ernaast loopt haar snelheid vinden. Het kost haar , dus haar snelheid is .

Als Julia tegen de band in loopt, is haar snelheid . Dus bereikt ze de andere kant van de loopband in: In het geval dat Julia met de loopband mee loopt, heeft ze een snelheid van . Dan bereikt ze de andere kant van de loopband in: Dus als Julia tegen de loopband in loopt, doet ze er de volgende tijd langer over dan als ze met de loopband mee loopt:

Antwoord:

We moeten eerst begrijpen hoe de groepen en er uitzien. De functie , ook de absolute waarde genoemd, geeft de afstand van de oorsprong to . Misschien is het niet direct duidelijk, maar de absolute waarde haalt het teken ( of ) van het getal weg. Kijk naar . Als en . In dit geval geldt . De conditie is dan hetzelfde als , dus . Dit is een lijn die en bevat, maar we zitten in het geval en , dus is het slechts het lijnstuk dat die punten verbindt. Met de andere gevallen van de tekens ( of ) van en erbij krijgen we dat groep bestaat uit lijnstukken die de punten en verbinden, die de punten en verbinden, die de punten en verbinden en die de punten and verbinden. Dit is een vierkant met als hoekpunten , , en .

Nu kijken we naar de groep . Die wordt bepaald door de vergelijking . Deze functie, maximum genoemd, neemt de grootste waarde aan van en . Om dit gelijk te krijgen aan , moet dus minstens een van en zijn, en moet de ander kleiner zijn. Als , dan geldt of . In dat geval moet , wat betekent dat . Voor geldt dit voor alle punten op het lijnstuk dat en verbindt, terwijl voor dit geldt voor alle punten op het lijnstuk dat en verbindt. we kunnen dit idee herhalen voor . dit voegt de lijnstukken die en verbinden en die en verbinden toe. Groep is dus ook een vierkant, met hoekpunten , , en .

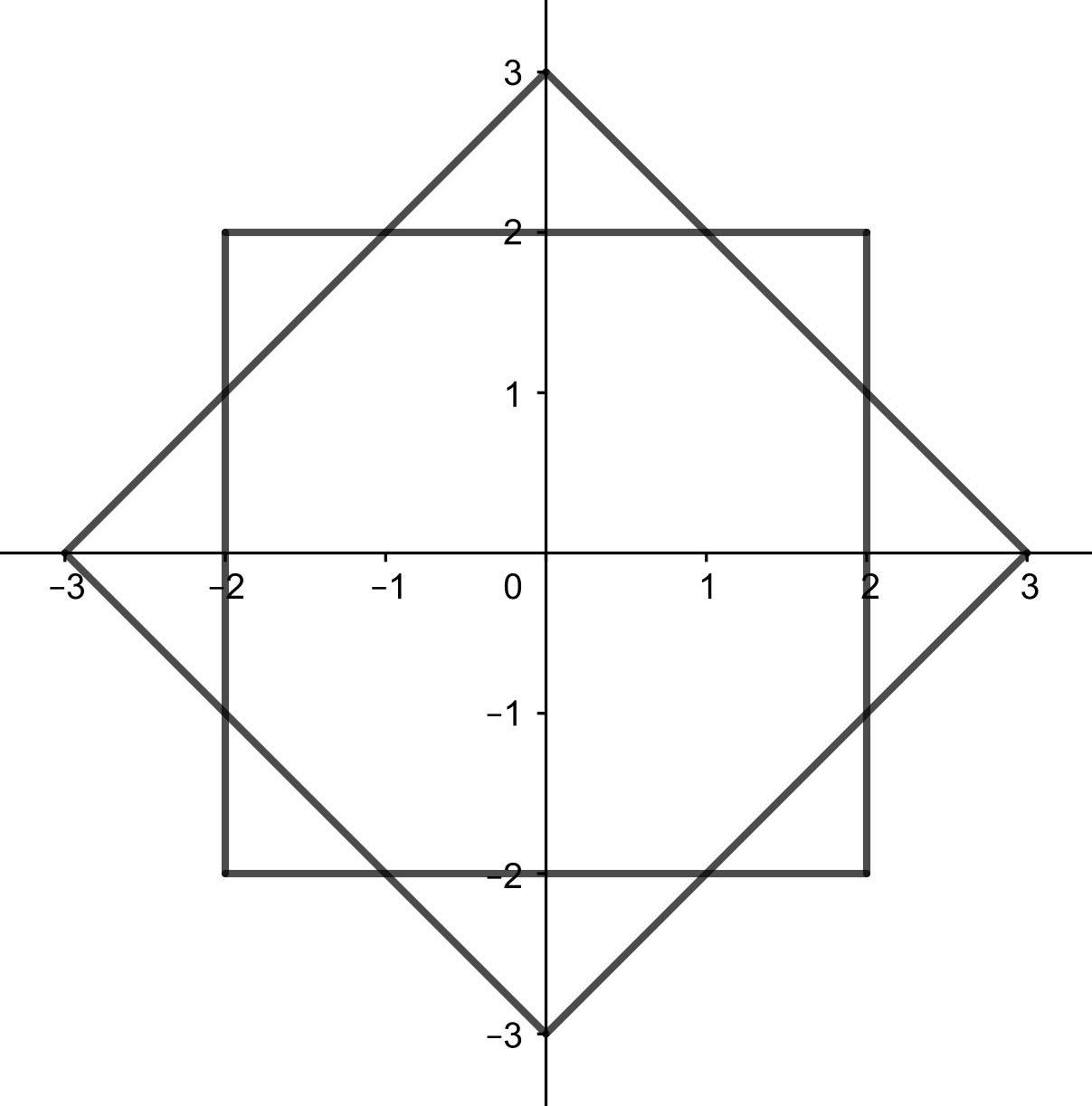
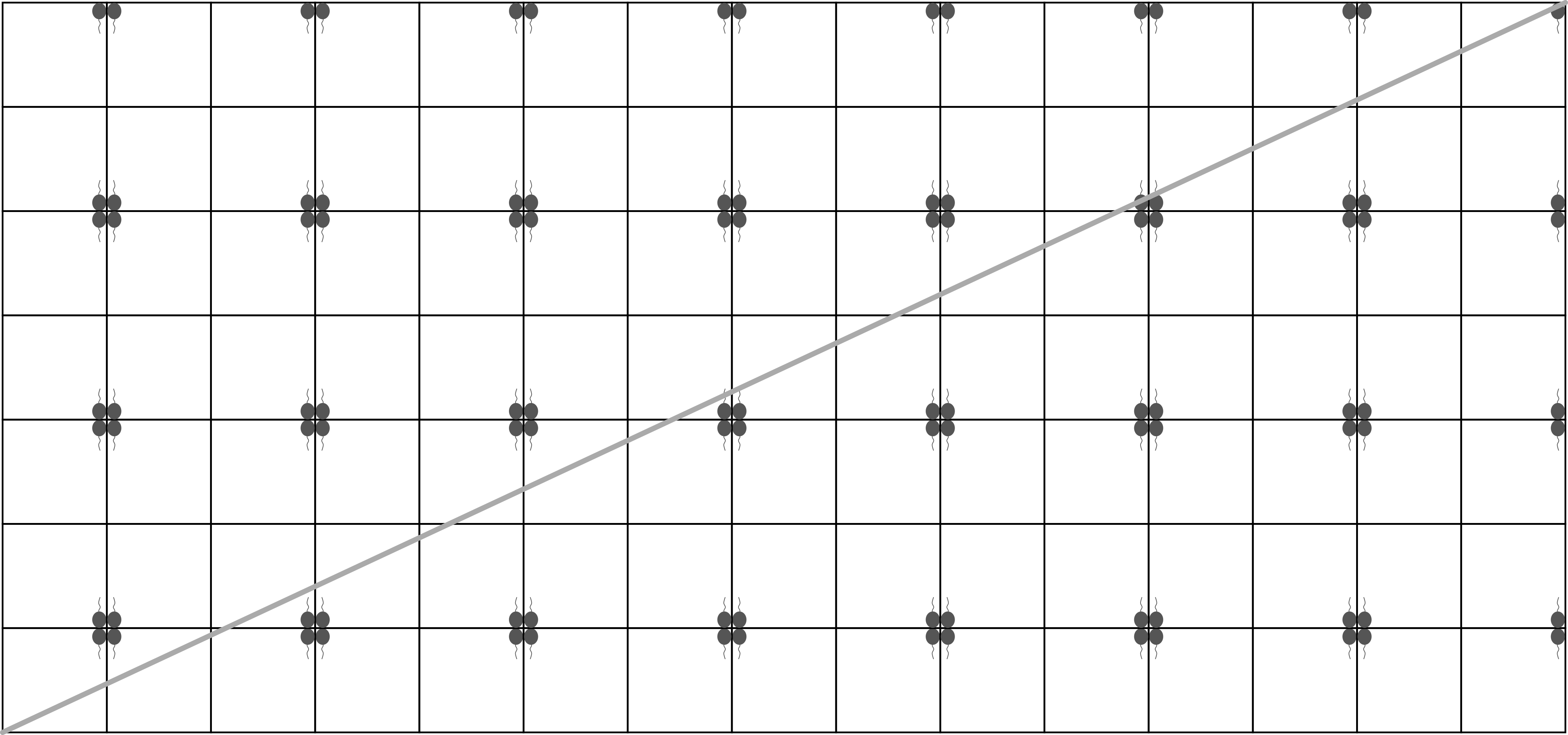
Groepen en zijn getekend in deze afbeelding:

In deze afbeelding kunnen we zien dat de vierkanten die met groep en overeenkomen in punten snijden, dus dat er punten in zowe groep als groep zitten.

Antwoord:

Zeg dat de linkertak bestaat uit weerstanden en de rechtertak uit . Dan moeten we dus berekenen. De weerstand van de rechtertak is , waar de waarde van één weerstand is. De weerstand van de linkertak is dan . Nu is de weerstand van de hele component: Volgens de opgave is dit een tiende van , de weerstand van de rechtertak. Hiermee kunnen we een vergelijking opstellen, waarmee we kunnen bepalen: Er zijn dus negen keer zoveel weerstanden in de rechtertak als in de linkertak.

Antwoord:

Marianne zal arbeid moeten verrichten om een steen met een massa van hoog genoeg op te tillen zodat de hele steen over de muur heen kan bewegen. We moeten dus uitzoeken wat de kleinst mogelijke afstand is waarmee we (het zwaartepunt van) de steen omhoog moeten verplaatsen.

Het zwaartepunt van een driehoek verdeelt de zwaartelijnen in twee lijnstukken met lengteverhouding , waar het langere lijnstuk aan een hoekpunt ligt. In een gelijkzijdige driehoek is een zwaartelijn tegelijk ook een hoogtelijn van een driehoek, zodat de zwaartelijnen lang zijn. De afstand van het zwaartepunt tot een zijde is dus . Dat betekent dat het middelpunt ten minste verwijderd is van elk willekeurig punt op de omtrek van de driehoek.

Op het moment dat het zwaartepunt van een driehoek (en dus ook het zwaartepunt van de steen) direct boven de muur ligt, is er een punt op de omtrek van de driehoek dat de muur raakt. Als dat niet zo was, dan hadden we de hele driehoek omlaag kunnen bewegen en hadden we zo minder arbeid kunnen verrichten. Dit punt is minstens verwijderd van het zwaartepunt van de driehoek. Dus als we de steen optillen langs de muur moeten we het zwaarepunt van een passende driehoek (en dus het zwaartepunt van de steen) tenminste tot boven de muur optillen. Het is ook mogelijk om het hiermee te doen - bijvoorbeeld door de steen horizontaal over de muur te verplaatsen met een zijkant parallel aan de bovenkant van de muur.

Dit betekent dat Marianne, terwijl ze de steen over de muur tilt, het zwaartepunt van de steen moet optillen om op gelijk niveau te zijn met de bovenkant van de muur, en dan nog om de steen over de muur heen te krijgen. In totaal moet ze dus het zwaartepunt optillen, zodat ze de potentiële energie van de steen vergroot met . Marianne verricht arbeid om deze extra potentiële energie aan de steen te geven, en verricht dus aan arbeid.

Antwoord:

Noem Andrews getallen en . Dan zijn de getallen op het bord en . Als een van de twee getallen en nul is, bijvoorbeeld als , dan zou de rekenkundige rij bestaan uit de getallen , , , . Nu zouden twee opeenvolgende termen in de rij en zijn, en zouden dus alle verschillen tussen opeenvolgende getallen moeten zijn. Met andere woorden: alle getallen zijn hetzelfde, dus . Maar dan zijn en hetzelfde en dat mag niet.

Dan kunnen we nu dus aannemen dat en beiden groter dan zijn. We kunnen ook aannemen dat . (Anders zouden we gewoon de namen omdraaien). Dan weten we dus dat het grootste getal op het whiteboard is en het daaropvolgende grootste getal is. Omdat een rekenkundige rij of stijgend of dalend is, moeten deze getallen dus opeenvolgend zijn in de rij. Dus alle opeenvolgende getallen moeten hetzelfde verschil hebben als en , namelijk . Het derde getal in de rij zou dus moeten zijn (want het verschil is ). Dan moet het laatste getal zijn, dat kleiner moet zijn dat . Dit geeft ons de volgende vergelijking: Als Andrew aan het begin de getallen en kiest, dan krijgt hij (met de som en het verschil) een rekenkundige rij , , , . Het enige wat we nog moeten doen is vinden hoeveel paren met er zijn zodat en beide eencijferige getallen zijn. Het is makkelijk te controleren dat de enige mogelijkheden voor zijn: , and . Andrew kon dus op drie manieren zijn getallen kiezen.

Antwoord:

Als Juraj aan het touw trekt, bewegen het gewicht en de katrollen die eraan bevestigd zijn een bepaalde afstand omhoog. Terwijl dit gebeurt, “verdwijnt” een deel van het touw van de katrollen omdat het deel uitmaakt van hetzelfde touw dat langs onze handen wordt verplaatst. Op het plaatje is afgebeeld wat er gebeurt als het gewicht wordt verplaatst van de onderste naar de bovenste lijn - in alle vijf de delen van het touw tussen de twee lijnen verdwijnt een even lang stuk touw. Als we het touw een stuk uittrekken, dan is de lengte van het stuk gelijk aan de som van de lengtes die op deze plekken verdwijnen. Het gewicht wordt dus een vijfde van de lengte van het stuk opgetild. Als we met een constante snelheid van aan het touw trekken, dan beweegt het gewicht met te snelheid .

Antwoord:

Laten we nog eens bedenken hoe we het kleinste gemene veelvoud en de grootste gemene deler van twee getallen kunnen bepalen. Eerst bepalen we de priemfactorisatie van beide getallen. Voor elk priemgetal doen we het volgende: aan het kgv voegen we dit priemgetal even vaak toe als het voorkomt in het getal waarin het het vaakst voorkomt, en aan de ggd voegen we dit priemgetal even vaak toe als het voorkomt in het getal waarin het het minst voorkomt. Hieruit kunnen we zien dat moet gelden voor elke natuurlijke getallen .

Neem nu voor en de twee getallen die aan Thomas’ voorwaarden voldoen. Voor deze getallen geldt dat en . Als we deze vergelijking combineren met het gegeven uit de vorige paragraaf krijgen we: Nu zijn zowel en dus veelvouden van 30, zodat we kunnen schrijven dat en voor natuurlijke getallen en . Merk op dat met maximale som overeenkomen met met maximale som .

Aangezien de ggd van de getallen en is, moet de ggd van en zijn. Bovendien weten we dat: De som van twee getallen met een bepaald product is zo groot mogelijk als de getallen zoveel mogelijk verschillen. Hun verschil is maximaal als en (of andersom). In dit geval is ook en hebben de getallen de maximale som . Als we dan weer kijken naar en , kunnen we zien dat de som van Thomas’ getallen is.

Antwoord:

Bekijk hoe bij deze opgaven de krachten staan. Er is de zwaartekracht op het zwaartepunt van de brug met massa . De grootte ervan is . Bovendien is er de kracht die de ketting uitoefent op de brug. De brug staat stil en draait dus ook niet. Dan moet de totale koppel op de brug dus nul zijn. De zwaartekracht die op een afstand van op de brug werkt veroorzaakt een koppel van . De verticale component van de kracht die de ketting uitoefent op de brug werkt op een afstand van en moet een koppel van teweegbrengen. Dus de grootte moet zijn: . Er zijn twee kettingen, dus beiden worden verticaal uitgerekt met een kracht .

Nu weten we de component van de kracht die de ketting in de verticale richting uitrekt. Maar hoe vinden we de kracht in de richting van de ketting? Merk op dat de driehoek die wordt gevormd door de ketting, poort en brug gelijkvormig is aan de driehoek die bestaat uit de krachten , en de vector die hun eindes verbindt. Dus de verhouding van de groottes van and moet gelijk zijn aan de verhouding van de hoogte van de poort en de lengte van de ketting. Deze lengte kunnen we berekenen met de stelling van Pythagoras: . Dus: Dus de spankracht in elke kabel is:

Antwoord:

Eerst berekenen we de kans dat het aantal enen in het bestand even is. Hiertoe bekijken we de eerste 2021 cijfers apart. Ze hebben een even of oneven aantal enen. Dan bepaalt de pariteit (even of oneven) van het laatste cijfer of de pariteit van de eerste 2021 cijfers verandert of hetzelfde blijft. De kans dat het verandert is even groot als de kans dat dat niet zo is omdat het alleen afhangt van het laatste cijfer, dat willekeurig is gekozen met een kans van om de pariteit te veranderen en kans om de pariteit van de eerste 2021 getallen hetzelfde te houden.

Nu beperken we ons tot reeksen cijfers met een even aantal enen. Hoeveel hiervan hebben een aantal enen dat deelbaar is door vier? Aangezien er een even aantal enen is, zijn er twee mogelijkheden - het aantal is ook deelbaar door vier of het heeft rest 2 na deling door vier. Neem twee verzamelingen en . bevat alle gevallen waar het aantal enen deelbaar is door vier, en alle gevallen waar de rest 2 is. Merk op dat we een reeks uit kunnen nemen en alle nullen naar enen kunnen veranderen en vice versa. Als het aantal enen eerst was en het aantal nullen , dan is na de verandering het aantal enen en het aantal nullen . Maar de rest van na deling door vier is 2. Dus de veranderde situatie maakt deel uit van . Als we weer terugveranderen, krijgen we weer een reeks uit verzameling (namelijk die waarmee we begonnen). Nu kunnen we dus alle mogelijkheden in paren opdelen, één uit en één uit . Elke mogelijkheid moet van een van de twee groepen deel uitmaken, en dus moeten de verzamelingen en evenveel mogelijkheden bevatten.

Dit betekent dat bij van de reeksen met een even aantal enen de kans op een aantal enen deelbaar door 4 is. Dat betekent dat de kansdat het aantal enen deelbaar is door vier gelijk is aan .

Antwoord:

Als we gewoon de eerste paar weerkaatsingen van de straal proberen te tekenen, komen we erachter dat de straal best vaak wordt herkaatst voordat hij de ballon raakt. Elke keer moeten we opnieuw berekenen waar de straal de muren raakt, was niet zo simpel is. Daarom proberen we iets anders.

Laten we - in plaats van de straal te reflecteren in een lijn die loodrecht op de muur staat in het raakpunt - steeds de hele kamer reflecteren in de muur die is geraakt. Dan nemen we aan dat er rechts van onze kamer een spiegelbeeld van de kamer is. Als we vervolgens de straal door de muur laten schijnen tot in de gespiegelde kamer, zal hij zich hetzelfde gedragen als in de originele kamer. Door dit steeds weer te herhalen als de straal een muur raakt, kunnen we zien dat de straal nu in een rechte lijn zal voortbewegen. Van de eerste weerkaatsing weten we dat de straal voor elke naar rechts omhoog beweegt. Op een gegeven moment zal de straal een van de hoekpunten van deze groep gespiegelde kamers raken, en als we geluk hebben is het de hoek hoek met de ballon (of een spiegelbeeld daarvan).

Een hoek wordt door de straal geraakt wanneer de afstand die de straal naar boven en naar rechts heeft afgelegd beiden een veelvoud van zijn. Als de straal omhoog beweegt, dan gaat hij naar rechts. Als een positief geheel getal is, dan is ook een geheel getal. We moeten dus de kleinste vinden zodat ook een veelvoud van is. Omdat , is de kleinste die voldoet . De situatie is dan zoals op de afbeelding hieronder is weergegeven:

We zien dat de straal ook echt de hoek met de ballon zal raken. Wat we nu nog moeten doen is het aantal weerkaatsingen berekenen. Een weerkaatsing gebeurt als onze straal naar een naburige kamer gaat. We zien dat de straal keer door een rechtermuur gaat en keer door een linkermuur. In totaal gaat hij dus keer door een muur. Dat betekent dat de straal dus keer weerkaatst moet zijn voordat hij de ballon raakte.

Deze afbeelding geeft weer hoe de straal (20 keer) weerkaatst wordt voordat hij de ballon raakt:

Antwoord:

Nadat er meel is toegevoegd aan het kleine glas (met grondvlak met een oppervlakte van ), is de zwaartekracht op het glass groter. Om het glas nog steeds te laten drijven, moet de drijfkracht evenveel zijn toegenomen. Met de wet van Archimedes krijgen we dat , waar de verandering in het verplaatste volume van het glas is. Dan krijgen we: Om het verplaatste volume te vergroten, moet de onderkant van het kleinere glas dieper liggen, en dus met een hoogteverschil dichter bij de bodem komen. Omdat dit gebeurt moet er een cylinder van water met volume zijn verplaatst, dat zich naar de zijkanten van het kleinere glas moet verplaatsen. Daar zal het de wateroppervlakte met stijgen. Het volume water dat wordt verplaatst kan worden uitgedrukt als , waar de oppervlakte van de onderkant van het grote glas is. Hiermee krijgen we de dat: Terwijl het kleine glas naar beneden beweegt zal de hoogte van het onder water liggende gedeelte van het glas stijgen met en als we het volume ervan berekenen, krijgen we de vergelijking: Als we deze vergelijkingen combineren krijgen we dat: Dus het wateroppervlak in het grotere glas stijgt met

Antwoord:

Het zou veel werk zijn om zoveel getallen op te tellen. Dus zoeken we een andere manier om de getallen op te tellen. Merk op dat we, als we bij een getal dat bestaat uit negens 1 optellen, we een getal krijgen dat bestaat uit een 1 gevolgd door nullen. We kunnen daarom de som herschrijven als .

Als we alle -1’en optellen krijgen we . De andere termen hebben als som , met 2022 enen. Het getal dat Susan krijgt is dit getal min 2022.

Hoe ziet dit getal eruit? 2022 aftrekken van heeft alleen een effect op de laatste 5 cijfers, die worden. De andere 2018 enen blijven hetzelfde. De cijfersom van Susans getal is .

Antwoord:

Noem de afmetingen van de baksteen en de massa . Dan zijn de verschillende waarden , en als volgt uit te drukken: Als we deze vergelijkingen met elkaar vermenigvuldigen krijgen we: Maar we weten dat het volume van de baksteen is. Dan herschrijven we de vergelijking als volgt: Merk tenslotte op dat de verhouding de dichtheid van de baksteen is. Hiermee kunnen we de massa van de baksteen bepalen: De massa van Bobs baksteen is .

Antwoord:

Zij het snijpunt van en . Aangezien en parallel lopen zijn driehoeken en gelijkvormig. De verhouding tussen de zijden van deze driehoeken is . Hiermee krijgen we de gelijkheden: Maar we weten dat en dat . Met deze vergelijkingen krijgen we dat: In driehoek geldt de vergelijking , dus met de stelling van Pythagoras moet het een rechte driehoek zijn met een rechte hoek bij . Dan is driehoek ook rechthoekig. De oppervlakte van het trapezium is gelijk aan het verschil tussen de oppervlaktes van deze driehoeken.

De rechthoekszijden van driehoek zijn en lang, dus de oppervlakte is . De rechthoekszijden van driehoek zijn a , dus de oppervlakte is .

Dan is de oppervlakte van het trapezium .

Antwoord:

Eerst lossen we een eenvoudigere opgave op, waarin Tessa maar 4 punten heeft gemarkeerd. Noem de punten , , and zodat ze op die volgorde op de cirkel liggen. De lijnstukken mogen elkaar niet snijden, ook niet op eindpunten. Dan moeten de lijnstukken allebei verschillende eindpunten hebben, en hebben we drie mogelijkheden:

1. en ,

2. en ,

3. en .

In het tweede geval snijden de lijnstukken elkaar, in de andere niet. Dus met vier punten hebben we precies twee manieren om de lijnstukken te tekenen.

Nu bekijken we weer het geval met 13 punten op de cirkel. Een paar lijnstukken zal vier verschillende eindpunten hebben. Op deze vier punten kunnen we het simpelere geval toepassen: als we vier punten hebben gekozen zullen we op twee manieren de lijnen kunnen tekenen.

Dan moeten we nu berekenen hoeveel mogelijkheden we hebben om vier punten te kiezen. Voor het eerste hebben we 13 mogelijkheden, voor het tweede 12, voor het derde 11 en voor het vierde 10. Maar nu hebben we elk viertal meerdere keren gekozen. We hebben het precies zovaak gekozen als er volgordes zijn waarop we de punten kunnen zetten. Voor de eerste positie hebben we 4 mogelijkheden, voor de tweede 3, voor de derde 2 en voor de laatste 1. Dan is het aantal manieren om vier punten uit te kiezen .

Omdat we voor elk viertal punten twee manieren hebben om het paar lijnstukken te tekenen, krijgen we dat Tessa de lijnstukken op manieren kan tekenen.

Antwoord:

Noem de massa van de blokken , , en de wrijvingscoëfficiënt . Bekijk de krachten die op de blokken werken. Ze werken als op de volgende afbeelding:

Op het plaatje zijn , and de zwaartekracht op de blokken. Omdat de bovenste twee blokken een kracht uitoefenen op het blok eronder zijn er normaalkrachten en . Het bovenste blok werkt met een naar beneden gerichte kracht met de grootte op het middelste blok. Volgens de derde wet van Newton krijgen we in hetzelfde punt een omgekeerde even grote normaalkracht van het middelste blok op het bovenste blok. Hetzelfde geldt voor het middelste en onderste blok met de kracht . Bovendien werkt de grond op het onderste blok met de normaalkracht .

In horizontale richting werken de krachten , die Marja zet op het onderste blok, en en , de spankracht in de touwen. Als laatste hebben we nog wrijvingskracht. Op het bovenste blok, dat naar rechts zou worden getrokken, werkt een wrijvingskracht naar links. De derde wet van Newton zegt dan dat het middelste blok moet werken op het bovenste blok met een kracht met de grootte van maar naar rechts gericht. De wrijvingskrachten tussen het middelste en onderste blok werken analoog, en de grond werkt het onderste blok met een wrijvingskracht .

Omdat elk blok in rust blijft (en dus niet versnelt) is de som van de krachten die erop werken nul in alle richtingen. Voor de krachten die in verticale richting werken krijgen we: En horizontaal krijgen we: De zwaartekrachten kunnen we berekenen met , waar de valversnelling is. Als Marja de maximale kracht zet, moeten de wrijvingskrachten ook maximaal zijn - als ze net iets meer kracht zou zetten, dan zou het systeem beginnen te bewegen en zouden de wrijvingskrachten hun maximale groottes bereiken. Hun grootte kan dan worden berekend als . Dan kunnen we alle onbekende grootheden uitdrukken met de bovenstaande vergelijkingen om te krijgen dat: Dus de grootst mogelijke kracht die Marjo kan zetten op het touw is: