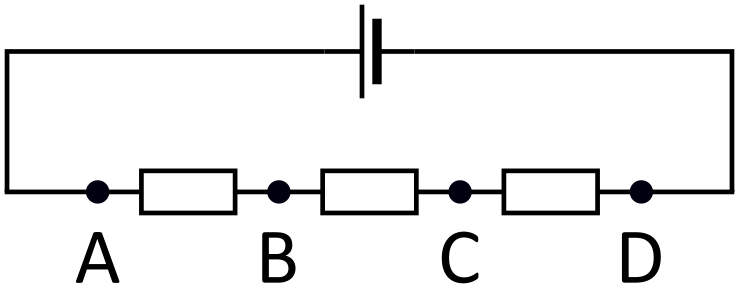
Antwoord:
Een spanning tussen twee punten beschrijft de grootte van het verschil van potentialen in deze twee punten. Het potentiaal beschrijft alleen de (elektrische) energie van een deelte met lading . Op elk van de punten , , , heeft dit deeltje een zekere potentiële energie en we kunnen dit getal aan elk van de punten toekennen. Dan beschrijven de spanningen enkel de verschillen tussen deze getallen.
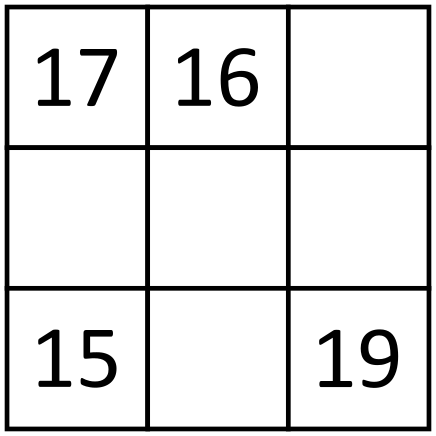
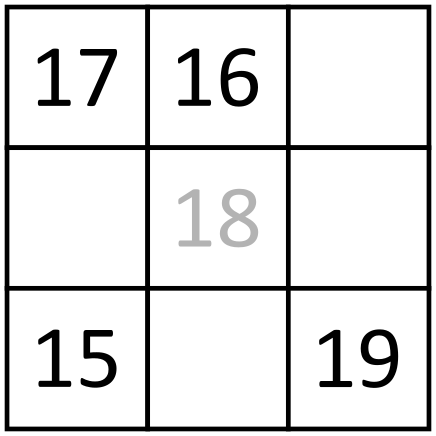
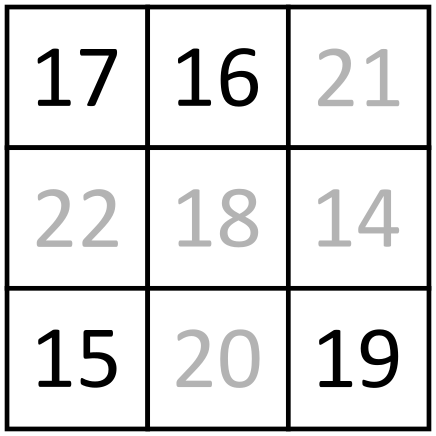
We kunnen nu het probleem herformuleren tot de wiskundige opgave van vier getallen toekennen aan , , en (nu hebben deze letters niks meer te maken met de natuurkunde opgave), zodat hun verschillen , , , , en de onbekende waarde zijn. Merk één interessante eigenschap op. Als je drie getallen neemt, zeg , en , zodat , dan is het verschil de som van de verschillen en (want ). Dus als we een willekeurig drietal getallen nemen, dan zullen hun verschillen de eigenschap hebben dat één de som van de andere twee is.
We kunnen nu teruggaan naar de opgave. Stel het onbekende verschil is het verschil tussen en . Neem de getallen , en . Elk van deze verschillen zijn bekend. Omdat één van deze de som van de andere twee moet zijn, hebben we enkel twee mogelijkheden: of . Iets vergelijkbaars moet gelden voor drietal , en , dus één van deze drietallen heeft verschillen , en en de andere heeft verschillen , en . De drietallen , , en , , overlappen enkel in en , dus dit verschil moet zijn (dit is het enige verschil waarin de drietallen , , en , , overlappen).
De getallen en spelen dezelfde rol, dus zonder verlies van algemeenheid kunnen we stellen dat de verschillen van en en van en respectievelijk en zijn. In het drietal , en weten we nu dat beide getallen en ofwel de grootste, ofwel het kleinste getal zijn. Kies ze zo, zodat de grootste is. We hebben nu twee mogelijkheden voor wat de verschillen van en de getallen en kunnen zijn.
Geval 1: Het verschil tussen en is . Dit betekent dat in het drietal , en , een van de getallen en het grootste en de andere het kleinste is. Maar in het drietal , en kozen we als grootste, dus is groter dan . Dus in het drietal , , weten we dat de grootste moet zijn. Dit alles betekent dat is groter is dan en groter is dan . Dus het verschill tussen en is . Dit is de eerste oplossing.
Geval 2: Het verschil tussen en is . Dit betekent dat in het drietal , en één van de getallen en het grootste en de andere het kleinste is. Op vergelijkbaar wijze met het vorige geval weten we dat groter is dan , dus moet de kleinste zijn. Dus weten we dat met kleiner is dan en dat met groter is dan . Dit betekent dat het verschil tussen en gelijk aan is. Dit is de tweede oplossing.
Om samen te vatten, we hebben gevonden dat het onbekende verschil enkel of kan zijn. In het originele probleem betekent dit dat de onbekende spanning enkel of kan zijn. Dus de som van de twee mogelijke onbekende spanningen is .





.png)

.png)



.png)

.png)