Probleemopgaven

Antwoord:

$2.45$

Matej betaalde met een $5€$ bankbiljet voor drie ijsjes, waarvan de totale prijs $0.80€+0.70€+1.05€=2.55€$ was. Dus de ijscoman gaf Matej $5€-2.55€=2.45€$ terug.

Antwoord:

$30$ $s$

Alle vier zijden van het vierkante deel zijn even lang, $0,5$ $m$. Alle zijden van het driehoekige dak hebben ook een onderling identieke lengte. Merk op dat een van de lijnen een zijde is van zowel het vierkant als de driehoek. Daarom moeten alle lijnen in de afbeelding dezelfde lengte hebben, dat wil zeggen $0,5$ $m$. De afbeelding bestaat uit zes van dergelijke lijnen en dus is de som van al hun lengtes $6\cdot 0,5m=3m$. Elke seconde trekt Naty $1$ $\mathrm{dm}$ lijn, dus voor elke $10$ seconde die is verstreken, trekt ze een lijn met een totale lengte van $10\cdot 1\mathrm{dm}=10\mathrm{dm}=1m$. Om het volledige plaatje te tekenen, moet ze drie keer zoveel tekenen, dus de tekening zal haar nemen $3\cdot 10s=30s$.

Antwoord:

$1050$ $g$

Ook al drijft het hout omdat het door een opwaartse kracht wordt ondersteund, dit heeft geen invloed op de gemeten massa. De weegschaal meet alleen de totale massa van de container en zijn inhoud, die niet wordt beïnvloed door krachten tussen de objecten in de container (aangezien deze objecten in rust zijn). Daarom kunnen we eenvoudig de massa’s van de objecten optellen: de container weegt $250$ $g$, een halve liter water weegt $500$ $g$ en het stuk hout weegt $300$ $g$. De schaal zal $250g+500g+300g=1050g$ meten.

Antwoord:

$10$

Laten we alle mogelijkheden opschrijven. Begin met wiskunde op de eerste plaats: MMPPP, MPMPP, MPPMP, MPPPM. Kijk nu naar de combinaties waar de natuurkunde eerst staat: PMMPP, PMPMP, PMPPM, PPMMP, PPMPM, PPPMM. Er zijn dus $10$ mogelijke dienstregelingen van Patric.

Antwoord:

$10$

Er is $3$ voet in $1$ yard en $12$ inch in $1$ voet. Dus $1$ yard is gelijk aan $3\cdot 12=36$ inches. Slakken moeten $100$ yards passeren, wat overeenkomt met $100\cdot 36=3600$ inches. Het duurt $10$ seconden om elke centimeter veld te passeren. Daarom duurt het $10\cdot 3600=36000$ seconden om het veld over te steken. Er zijn $60$ minuten in elk uur en $60$ seconden in elke minuut. Dus $1$ uur = $60\cdot 60=3600$ seconden. Als gevolg hiervan heeft de slak $36000÷3600=10$ uur nodig om het hele veld over te steken.

Antwoord:

$81$

Als we het getal $111111111$ met zichzelf vermenigvuldigen, krijgen we nummer $12345678987654321$. De som van de cijfers van dit nummer is $1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1=81$.

Antwoord:

$46$

Laten we eerst tellen hoeveel vierkanten volledig zijn gevuld. Er zijn $40$ volledig gevulde vierkanten, overeenkomend met $40$ gram inkt. Naast deze vierkanten zijn er enkele gedeeltelijk gevulde vierkanten. Als we alle volledig gevulde vierkanten van de afbeelding verwijderen, zien we $6$ geverfde driehoeken.

Alle driehoeken op dezelfde verticale lijn kunnen worden gekoppeld om $3$ verschillende rechthoeken te vormen. De eerste rechthoek beslaat $3$ vierkanten; de tweede beslaat $2$ vierkanten en de derde beslaat $1$ vierkanten. Om ze te vullen is $3+2+1=6$ gram inkt nodig. Daarom heeft Susan $46$ gram inkt nodig om het hele plaatje te schilderen.

Antwoord:

$8$ $\mathrm{km}∕h$

Als Adam zijn tempo aanhield, zou hij $20$ keer $400m$ rennen en dus $20\cdot 400m=8000m$ in één uur. Dit komt overeen met de snelheid van $8$ $\mathrm{km}∕h$. Hoe zit het met zijn gemiddelde snelheid? Aangezien Adam zijn snelheid de eerste $20$ minuten niet veranderde, moet $8$ $\mathrm{km}∕h$ zijn gemiddelde snelheid zijn geweest. Zijn gemiddelde snelheid tijdens de eerste $20$ minuten was dus $8$ $\mathrm{km}∕h$.

Antwoord:

$5$

Een enkele reis tussen twee eindstations duurt

. Daarom duurt een terugreis van een willekeurige bus $2\cdot 24\min =48\min$. Als we willen dat de passagiers nooit langer dan $10$ $\min$ wachten, moeten er op het moment dat de eerste bus arriveert minstens $4$ verschillende bussen het station verlaten. Er zijn dus vijf bussen nodig.

Antwoord:

$101$

Als Jaro de printer vanuit de vergaderruimte gebruikt, verspilt hij tijd door alleen maar terug te gaan naar zijn kantoor, namelijk één minuut. Om liever in de vergaderruimte te printen, moet hij een bepaald aantal pagina’s printen zodat de printer in de vergaderruimte minstens $1$ minuut sneller is dan de printer van Jaro’s kantoor. Dat betekent dat als Jaro zowel in zijn kantoor als in de vergaderruimte tegelijkertijd hetzelfde aantal pagina’s begint te printen, op het moment dat de printer in de vergaderruimte stopt, de printer op kantoor nog minimaal één minuut langer moet printen. Merk op dat de printer op kantoor $20$ pagina’s per minuut afdrukt en dat de printer in de vergaderruimte $25-20=5$ pagina’s per minuut sneller is. Daarom moet de printer op kantoor minstens $4$ minuten blijven afdrukken om $20$ pagina’s achter te laten op de snellere printer, en dus moet het totale aantal pagina’s meer dan $100$ pagina’s zijn. Daarom is het voor Jaro sneller om de printer vanuit de vergaderruimte te gebruiken bij het afdrukken van minimaal $101$ pagina’s.

Antwoord:

$995$

Bij afronding op tientallen is het maximale verschil tussen het resultaat en Pedro’s favoriete getal $5$. Het kleinste positieve gehele getal dat het resultaat kan zijn van afronding op duizendtallen is $1000$. Dus Pedro’s favoriete nummer moet minstens $1000-5=995$ zijn. Men kan gemakkelijk merken dat $995$ aan alle eisen voldoet.

Antwoord:

$50$

Nina liep twee ronden, dus de totale afstand is $2\cdot 6\mathrm{km}=12\mathrm{km}$, met gemiddelde snelheid $8$ $\mathrm{km}∕h$. Daarom moet de totale duur van de run zijn:

Aangezien Nina de eerste ronde in $40$ minuten liep, moest ze de tweede ronde in $90-40=50$ minuten lopen.

Antwoord:

$12$

De gebeurtenis dat iemand verloor, gebeurde precies $10+9+8=27$ keer – dit moet het totale aantal gespeelde games zijn. Daarom moet het totale aantal gewonnen games ook $27$ zijn. Dit betekent dat Constance $27-7-8=12$ games moest winnen.

Antwoord:

$1$kg

De lange arm van elke hefboom is tweemaal de korte arm. Daarom moet, om elke hefboom in evenwicht te brengen, de massa van alles dat aan het korte uiteinde wordt gehangen, tweemaal de massa zijn van alles dat aan het lange uiteinde wordt opgehangen. Aan het korte uiteinde van de eerste hendel bevindt zich het gewicht $18$ $\mathrm{kg}$. Aan het lange uiteinde hangt de tweede hendel, wat betekent dat de massa van alles wat aan de tweede hendel wordt gehangen $18\mathrm{kg}:2=9\mathrm{kg}$ moet zijn. Op de tweede hendel hebben we een ander gewicht, evenals de derde hendel. Evenzo, om de tweede hendel in balans te brengen, moeten we het gewicht (op de korte arm) twee keer zo zwaar hebben als de derde hendel (op de lange arm). Daarom zal dat gewicht massa $6$ $\mathrm{kg}$ hebben en de twee gewichten op de derde hefboom een gecombineerde massa van $3$ $\mathrm{kg}$. Tenslotte verdelen we deze massa over de twee gewichten in de gebruikelijke $2:1$ verhouding. We vinden dat het gewicht aan het lange uiteinde van de derde hefboom $1$ $\mathrm{kg}$ weegt.

Antwoord:

$40$

Als het water niet wegliep in het opvangsysteem en niet over de randen van het dak zou lopen, zouden we aan het einde van de regenbui een blok water op het dak aantreffen. Ervan uitgaande dat de regen even dicht over het zwembad is gevallen als over het dak, zal de waterspiegelstijging in het zwembad gelijk zijn aan de hoogte van dit denkbeeldige waterblok op het dak. Het waterblok heeft volume $4000L=4000{\mathrm{dm}}^3=4m^3$. De oppervlakte van de basis is gelijk aan de oppervlakte van het dak: $100$ $m^2$. We weten dat het volume van het blok het product is van de hoogte en het basisoppervlak. Daarom is de hoogte $\frac{4m^3}{100m^2}=0,04m=40\mathrm{mm}$. Hierdoor is het waterpeil in het zwembad gestegen met $40$ $\mathrm{mm}$.

Antwoord:

$22$

De voorwaarde dat de getallen in aangrenzende cellen ten minste $2$ verschillen, betekent dat getallen die slechts $1$ verschillen, niet naast elkaar kunnen liggen.

Laten we eens kijken naar de tweede en derde cel in de middelste rij. Beide cellen grenzen aan alle andere cellen behalve één. Welke getallen kunnen we op deze cellen plaatsen? Alleen getallen, die $1$ verschillen van precies één ander getal in het bereik $1$ - $8$. Het is duidelijk dat alleen de nummers $1$ en $8$ aan deze voorwaarde voldoen. Vanwege de symmetrie van de tablet maakt het niet uit in welke volgorde we die nummers plaatsen, en dus doen we het op deze manier:

Nummers $1$ en $8$ hebben beide slechts één ander nummer waarvan ze verschillen met $1$. Dat zijn respectievelijk $2$ en $7$. We moeten daarom $2$ en $7$ in de overige twee cellen van de middelste rij plaatsen.

De cel met nummer $2$ kan niet grenzen aan de cel met nummer $3$, die dus boven of onder nummer $1$ moet liggen. Om vergelijkbare redenen moet het nummer $6$ zich boven of onder het nummer $8$ bevinden. Dit laat ons twee mogelijkheden over. Als we zowel $3$ als $6$ in één rij plaatsen, zullen we in de resterende rij getallen $4$ en $5$ naast elkaar moeten plaatsen, wat verboden is. We moeten dus voor de tweede optie gaan, bijvoorbeeld $3$ en $6$ in verschillende rijen plaatsen. Nu merken we dat $4$ en $3$ niet naast elkaar kunnen liggen, wat precies één manier laat om de tabel in te vullen:

Ten slotte berekenen we dat de som van de getallen die grenzen aan de cel met het getal $4$ $22$ zal zijn.

Antwoord:

$250$ $m$

Laten we voor het gemak de snelheid veranderen van kilometers per uur naar meters per seconde:

De trein met snelheid $30$ $m∕s$ die zich voor $75$ $s$ voortbeweegt, passeert afstand $75s\cdot 30m∕s=2250m$. Daarom passeert de locomotief $2250$ $m$ vanuit de tunnel. Omdat de tunnel $2000$ $m$ lang is, was de locomotief na $75$ seconden $2250m-2000m=250m$ achter de tunnel. De trein moet $250$ $m$ lang zijn.

Antwoord:

$57$ $\mathrm{mm}$

Aangezien het gemiddelde van Ella’s potloden $12$ $\mathrm{mm}$ is, moet de som van hun lengte $6\cdot 12\mathrm{mm}=72\mathrm{mm}$ zijn. Om een bepaald potlood het langste te maken, moet het andere $5$ zo kort mogelijk zijn. Daarom moeten ze respectievelijk de lengten $1$ $\mathrm{mm}$, $2$ $\mathrm{mm}$, $3$ $\mathrm{mm}$, $4$ $\mathrm{mm}$, $5$ $\mathrm{mm}$ hebben, wat in totaal $15$ $\mathrm{mm}$ is. Voor het langste blijft potlood $72\mathrm{mm}-15\mathrm{mm}=57\mathrm{mm}$.

Antwoord:

$4$ $m$

Door het behoud van energie verliest de steen een kinetische energie als gevolg van een werkende kracht die een werk op de steen doet. Aanvankelijk heeft de steen met massa $m=18,6\mathrm{kg}$ en snelheid $v=2m∕s$ een kinetische energie $E_k=\frac{1}{2}m{v}^2$. De kracht die de steen afremt is de wrijvingskracht $F_t$, die gelijk is aan het product van de normaalkracht van het ijs en de wrijvingscoëfficiënt $f$. In deze situatie is de normaalkracht de zwaartekracht van de aarde $F_G=\mathit{mg}$ waarbij $g$ de zwaartekracht van de aarde is. Als de steen een afstand verschuift $s$, werkt de wrijvingskracht op de steen $W=F_{t}s=F_G\mathit{fs}=\mathit{mgfs}$. Als de steen stopt met glijden, heeft hij een snelheid van nul en dus ook geen kinetische energie. Dan kunnen we de afstand $s$ als volgt berekenen:

Gezien de bovenstaande waarden zal de steen een afstand van $s=\frac{{(2m∕s)}^2}{2\cdot 0.05\cdot 2m∕s^2}=4m$ van Jim’s hand afschuiven.

Antwoord:

$50\circ$

Aangezien de punten $A$ en $D$ op middelloodlijn van lijnstuk $\mathit{BC}$ liggen, zien we dat de driehoeken $\mathit{ABC}$ en $\mathit{DBC}$ gelijkbenig zijn met basis $\mathit{BC}$. Met behulp van dit feit kunnen we de maten van hoeken aan de basis berekenen in driehoek $\mathit{ABC}$ als $\frac{180\circ -40\circ }{2}=70\circ$ en in driehoek $\mathit{DBC}$ als $\frac{180\circ -140\circ }{2}=20\circ$. Vandaar dat de maat van een hoek $\mathit{ACD}$ $|\measuredangle \mathit{ACD}|=|\measuredangle \mathit{ACB}|-|\measuredangle \mathit{DCB}|=70\circ -20\circ =50\circ$ is.

Antwoord:

$2$ $\mathrm{kg}$

De verbrandingswarmte van hout is $21\mathrm{MJ}∕\mathrm{kg}=21000\mathrm{kJ}∕\mathrm{kg}$. Aangezien de efficiëntie van het verbranden van hout in een kampvuur slechts $0.5\%$ is, krijgen we door het verbranden van één kilogram $21000\mathit{kJ}∕\mathit{kg}\cdot 0.005\cdot 1\mathit{kg}=105\mathit{kJ}$ energie. Om het water aan de kook te brengen, dat wil zeggen door de temperatuur te verhogen van $0\circ$C naar $100\circ$C, heeft Kate een energie nodig van $(100\circ C-0\circ C)\cdot 4.2\mathit{kJ}∕(\mathit{kg}\cdot \circ C)\cdot 0.5\mathit{kg}=210\mathit{kJ}$, wat precies twee keer $105\mathit{kJ}$ is. Daarom heeft Kate $2\mathit{kg}$ hout nodig.

Antwoord:

$68$

Geef A aan als het aantal appelsnoepjes en B als het aantal bananensnoepjes. In het begin waren er twee keer zoveel appelsnoepjes als bananensnoepjes, wat betekent $A=2\cdot B$. Nadat Lenka $17$ appel en $17$ bananensnoepjes had gegeten, had ze drie keer meer appelsnoepjes dan bananensnoepjes, wat $A-17=3\cdot (B-17)$ betekent. Als we $A$ vervangen door $2\cdot B$ (dit weten we uit de eerste vergelijking) krijgen we:

Daarom zaten er aanvankelijk $34$ bananensnoepjes en $68$ appelsnoepjes in de verpakking.

Antwoord:

$20$

Laten we eerst eens kijken naar Jerry’s eerste zin. Als het waar was, zou het zelf Jerry’s enige ware zin zijn, dus haar tweede zin zou onwaar moeten zijn. Als de eerste zin onwaar was, zou de tweede zin weer niet waar kunnen zijn - anders zou de eerste zin ook waar moeten zijn. We kunnen dus met zekerheid zeggen dat Jerry’s tweede zin onwaar is. Maar over haar eerste zin kunnen we nog niets zeggen.

Jerry’s tweede zin is onjuist. Daarom moet Marcel één ware en één valse zin hebben gezegd. Laten we bespreken wat er zou gebeuren als zijn eerste of zijn tweede zin de ware zou zijn.

Als het waar zou zijn dat "alle verdachten minstens één valse straf hebben uitgesproken", dan zou Marcels zin, dat hij de Naboj niet heeft, onjuist zijn. Daarom zou hij de dief moeten zijn. Maar dan zouden beide zinnen van Matthew waar moeten zijn, wat onmogelijk zou zijn, aangezien we de zin van Marcel "alle verdachten hebben minstens één valse zin" als correct beschouwen.

Daarom moet de ware zin Marcels tweede zin zijn, dat hij de Naboj niet heeft, en omdat zijn eerste zin onwaar is, moet er iemand zijn die twee ware zinnen heeft gezegd. Dat kan nu alleen Majo of Matthew zijn. Maar aangezien Marcel de Naboj niet heeft, kan Matthew geen twee ware zinnen hebben gezegd. Daarom is degene wiens beide zinnen waar zijn Majo, die zegt dat Matthew de Naboj heeft. Daarom is Matthew de dief.

Ten slotte moeten we onderzoeken hoeveel zinnen correct kunnen zijn. We hebben bewezen dat beide zinnen van Majo waar waren. Van de zinnen van Matthew was alleen de tweede correct. Evenzo was alleen de tweede zin van Marcel correct. We zien nu dat Jerry’s eerste zin waar of onwaar kan zijn. Er kunnen dus $4$ of $5$ ware zinnen zijn geweest. De som van mogelijke hoeveelheden ware zinnen is dus $4\cdot 5=20$.

Antwoord:

$216$ $J$

Boeken op de vloer vormen een balk met een hoogte van $8\cdot 5\mathrm{cm}=40\mathrm{cm}$, dus hun zwaartepunt bevindt zich ter hoogte van $20\mathrm{cm}=0,2m$ boven de grond. Als de boeken op de plank zouden worden geplaatst, zouden ze een balk vormen met een hoogte van $20$ $\mathrm{cm}$ en het zwaartepunt op de hoogte $10\mathrm{cm}=0,1m$ boven de plank. Aangezien de plank $1,6$ $m$ boven de grond is, is het verschil in de hoogte van het zwaartepunt van de boeken voor en na het optillen op de plank $1,6m-0,2m+0,1m=1,5m$. Het volume van de boeken is $15\mathrm{cm}\cdot 20\mathrm{cm}\cdot 40\mathrm{cm}=12000{\mathrm{cm}}^3=12{\mathrm{dm}}^3$ en hun dichtheid is $1200\mathrm{kg}∕m^3=1,2\mathrm{kg}∕{\mathrm{dm}}^3$. Daarom is hun massa $12{\mathrm{dm}}^3\cdot 1,2\mathrm{kg}∕{\mathrm{dm}}^3=14,4\mathrm{kg}$. Het verschil in potentiële energie tussen de boeken op de grond en op de plank is dan gelijk aan $14,4\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 1,5m=216J$. Dat betekent dat Maria een werk van $216$ $J$ moet doen.

Antwoord:

$51$ $\mathrm{cm}$

Het belangrijkste aspect van dit probleem is om te onthouden dat voor elke driehoek de driehoeksongelijkheid geldt. In het bijzonder zegt de driehoeksongelijkheid dat de som van elke twee zijden van een gegeven driehoek strikt groter moet zijn dan de derde zijde. Laten we eens kijken naar de twee kortere zijden van de driehoek: $\mathit{BC}$ en $\mathit{AC}$,. We weten dat hun lengte respectievelijk maximaal $8$ $\mathrm{cm}$ en $18$ $\mathrm{cm}$ kan zijn. Op basis hiervan kunnen we stellen dat wil de driehoek überhaupt bestaan, zijn derde zijde korter moet zijn dan $8\mathrm{cm}+18\mathrm{cm}=26\mathrm{cm}$, dus hoogstens $25$ $\mathrm{cm}$. De driehoek met zijden van $8$ $\mathrm{cm}$, $18$ $\mathrm{cm}$ en $25$ $\mathrm{cm}$ voldoet aan de driehoeksongelijkheid en kan dus bestaan. Bovendien hebben de twee kortere zijden hun maximaal toegestane lengte en moet de derde zijde korter zijn dan de som van die twee, dus de omtrek van $8\mathrm{cm}+18\mathrm{cm}+25\mathrm{cm}=51\mathrm{cm}$ is de grootst mogelijke.

Antwoord:

$5600$ $\mathrm{kJ}$

Kinetische energie neemt toe met de tweede macht van de snelheid. Dus om $3$ keer hogere snelheid te krijgen moet men $3\cdot 3=9$ keer meer energie verbruiken. Om dus van nul naar $120$ $\mathrm{km}∕h$ te accelereren, heeft Sabine $9\cdot 700\mathrm{kJ}=6300\mathrm{kJ}$ energie nodig. Om te versnellen van $40$ $\mathrm{km}∕h$ naar $120\mathit{km}∕h$ gebruikte Sabine $6300\mathrm{kJ}-700\mathrm{kJ}=5600\mathrm{kJ}$ energie.

Antwoord:

$1$

Laten we alle getallenparen uit het eerste artikel onderzoeken. We beginnen met paren die nummer $1$ bevatten. De verschillen in getallen tussen deze paren zijn precies alle getallen van $1$ tot $99$. Laten we vervolgens kijken naar alle paren die $2$ bevatten maar niet $1$ (of als alternatief, paren waarbij $2$ het kleinste getal is). De verschillen in getallen tussen deze paren zijn precies alle getallen van $1$ tot $98$. Op dezelfde manier kunnen we doorgaan totdat we alle paren bekijken waarbij $99$ het kleinste getal is; in zo’n geval hebben we maar één paar waarvan het aantalverschil $1$ is. In al deze gevallen was alleen nummer $1$ altijd een van de verschillen, en daarom verschijnt het nummer $1$ het vaakst op het tweede vel papier.

Antwoord:

$10$

Laten we zeggen dat er $n$ weerstanden zijn en dat elke weerstand weerstand $R$ heeft. Wanneer we de multimeter op één weerstand aansluiten, meten we de weerstand in een schakeling met parallel geschakelde weerstanden. In de ene tak hebben we $1$ weerstand en in de tweede tak $n-1$ weerstanden. Evenzo, als we de multimeter op twee weerstanden aansluiten, hebben we $2$ weerstanden in één tak en $n-2$ weerstanden in de tweede. Dit leidt ons naar het stelsel vergelijkingen:

Na vermenigvuldiging van de vergelijkingen met de noemers krijgen we het stelsel:

Als we de haakjes uitbreiden, krijgen we:

Trek nu de tweede vergelijking van de eerste af:

Dus de getalswaarde van weerstand van een weerstand in ohm is gelijk aan het aantal weerstanden. Deel de hele vergelijking door ohm en vul deze informatie in de vergelijking $\mathit{nR}-R=9n\mathrm{\Omega }$:

Daarom zijn er ofwel $n=0$ of $n=10$ weerstanden. De behuizing $n=0$ slaat echter nergens op, dus er moeten $n=10$ weerstanden zijn geweest.

Antwoord:

$14$

Onderscheid de gevallen afhankelijk van het hoekpunt waarmee het hoekpunt is verbonden $A$. Als het hoekpunt $A$ verbonden is met enkele van de hoekpunten $C$, $E$ of $G$, dan verdeelt dit lijnsegment de andere hoekpunten in twee groepen met een oneven aantal hoekpunten. Ze kunnen echter niet in paren worden verdeeld, dus we kunnen geen lijnsegmenten tekenen die voldoen aan de voorwaarden van het probleem. Als het hoekpunt $A$ verbonden is met hoekpunt $B$, blijven de andere $6$ hoekpunten over die verbonden moeten worden. We hebben deze $5$ manieren om dat te doen:

We zouden vergelijkbare $5$ manieren krijgen als we vertex $A$ zouden verbinden met vertex $H$. Als we het hoekpunt $A$ met het hoekpunt $D$ zouden verbinden, zouden we meteen de hoekpunten $B$ en $C$ moeten verbinden. Voor de andere $4$ hoekpunten hebben we deze twee manieren:

Analoog krijgen we $2$ manieren als we hoekpunten $A$ en $H$ verbinden. We hebben alle gevallen overwogen, met welk hoekpunt het hoekpunt $A$ kan worden verbonden, dus er zijn precies $5+5+2+2=14$ manieren waarop Laura de lijnsegmenten kan tekenen.

Antwoord:

$4000$ $\mathrm{kg}∕m^3$

Als we een vat met massa $m_{\mathit{vessel}}=250g$ op de schaal zetten en water met volume $V=0,5L$ erin gieten, geeft de schaal massa aan:

Na het inbrengen van een kiezelsteen aan een touwtje toonde de weegschaal massa $m=1\mathrm{kg}$. Wat veroorzaakte de toename van de massa? Twee krachten werken op de kiezelsteen - zwaartekracht en drijvend. Het is de opwaartse kracht waarmee het water op de kiezelsteen inwerkt. Volgens de wet van actie-reactie moet de kiezelsteen op het water inwerken met een kracht van dezelfde grootte maar met tegengestelde richting. Dit is de enige kracht die de massa zal veranderen, zoals de schaal aangeeft. De grootte van kracht $F$, op basis waarvan de schaal de massa aangeeft, moet dan gelijk zijn aan de som van de grootte van de zwaartekracht $F_G$ en de grootte van de opwaartse kracht van water op kiezelsteen $F_b$:

Hieruit halen we dat het volume van kiezel is:

Uit de tweede weging weten we dat de massa van de kiezelsteen $m_{\mathit{pebble}}=1\mathit{kg}$ is. Daarom moet de dichtheid van de kiezelsteen zijn:

Antwoord:

$6$ $m∕s$

Terwijl Winnie de Poeh naar beneden glijdt, blijft de totale mechanische energie behouden. De afname van potentiële energie van Pooh moet dus gelijk zijn aan zijn kinetische energie. De afname van de hoogte is $\mathrm{\Delta }h=a{x}^2$. Dit moet dus gelden:

Wanneer we de waarden uit de probleemstelling vervangen, realiseren we ons dat Pooh snelheid zal hebben:

Antwoord:

$18$

Drie van de zijkanten van de originele kubus moesten blauw worden geverfd en drie moesten oranje zijn. Wat meer is, om overstaande zijden tegenovergestelde kleuren te laten hebben, moeten alle drie de zijden van dezelfde kleur één gemeenschappelijk hoekpunt hebben gehad. Laten we dus eens kijken welke kleine kubussen een blauwe en een oranje kant kunnen hebben. Dat soort kubus moet een rand gemeen hebben met de originele kubus - een rand die werd gedeeld door een blauwe en een oranje zijde van de originele kubus. Langs elke dergelijke rand van de oorspronkelijke kubus werden $5$ kleinere kubussen gemaakt. Maar daarvan hebben $2$ ook een gemeenschappelijk hoekpunt met de initiële kubus, en dus hebben ze eigenlijk een derde geschilderde zijde. Daarom zullen er langs elke dergelijke rand van de initiële kubus, waar de blauwe en oranje zijde samenkomen, slechts $5-2=3$ kleine kubussen zijn die precies 1 blauwe en precies 1 oranje zijde hebben. Van de randen van de originele kubus zijn er $6$ randen waar een blauwe en een oranje kant samenkomen, vandaar dat er $6\cdot 3=18$ kleine kubussen zijn van het soort dat we zoeken.

Antwoord:

$1413$

Merk op dat wanneer we $2021$ van tweeën vermenigvuldigen met $2021$ van vijfen, het resultaat de vermenigvuldiging van $2021$ tienen zou zijn. We kunnen gemakkelijk zeggen hoe dit getal eruit ziet - het begint met cijfer één, gevolgd door $2021$ nullen. Het product van $2021$ getallen tien bevat dus $2022$ cijfers.

Kijk vervolgens naar het aantal cijfers van het product van twee getallen. Het aantal cijfers van een product is ofwel de som van het aantal cijfers van de factoren of de som van het aantal cijfers van de factoren min één. Merk op dat het laatste geval alleen gebeurt als de twee factoren klein zijn, zodat we geen tien overdragen op de hoogste positie.

Het getal dat begint met cijfer één gevolgd door $2021$ nullen is het kleinste getal met $2022$ cijfers. Het kan op twee manieren worden gecreëerd. Ofwel hebben we twee getallen vermenigvuldigd die beginnen met cijfer één, gevolgd door alleen nullen, of we hebben een tien overgenomen. We hebben ons $2022$-cijferige getal als een product van getal dat een product is van $2021$ nummer twee en een getal dat een product is van $2021$ nummer vijf. Daarom moeten we een tien hebben overgedragen. Dit betekent dat deze factoren $2022$ cijfers hebben gecombineerd. We weten dat het getal dat een product is van $2021$ getallen twee, $609$ cijfers heeft. Vandaar dat het aantal cijfers van het getal dat het product is van $2021$ getallen vijf en dat Adams computer teruggeeft, $2022-609=1413$ is.

Antwoord:

$60$ $g$

Als de zuigers niet bewegen, moet er van beide kanten dezelfde kracht op de zuiger werken, dus de som van de krachten is $0$. Omdat de zuiger aan beide zijden hetzelfde oppervlak heeft, moet er dezelfde druk op de zuiger staan. De druk die op de kleine zuiger werkt vanuit de richting van de zuiger met water, heeft twee componenten: hydrostatische druk en druk veroorzaakt door externe kracht (gewicht van het object op 1. zuiger). Hydrostatische druk van de waterkolom met hoogte $h_1=20\mathrm{cm}$ is:

Druk geïnduceerd door object met gewicht $m_1=100g$ geplaatst op zuiger met oppervlakte $S_1=10{\mathrm{cm}}^2$ is:

Evenzo zijn hydrostatische druk van oliekolom met hoogte $h_2=30\mathrm{cm}$ en druk veroorzaakt door object met onbekend gewicht $m_2$ op zuiger met oppervlakte $S_2=20{\mathrm{cm}}^2$:

Zoals we zeiden $p_{h1}+p_{t1}=p_{h2}+p_{t2}$. Dus we kunnen zeggen:

Vanaf hier kunnen we $m_2$ uitdrukken:

Matej moet een object met gewicht $60$ $g$ op de tweede zuiger plaatsen.

Antwoord:

$15$

Laten we eerst de twee personen kiezen die de stoelen niet hebben gewisseld. Deze twee personen verdelen de rest van de mensen in drie groepen - links van beide vaste stoelen, in het midden tussen de vaste stoelen en rechts van beide vaste stoelen. In zo’n indeling beschouwen we een groep van geen mensen toch als een "groep". Merk op dat een lid van elke groep op een stoel moet gaan zitten die vroeger toebehoorde aan een ander lid van dezelfde groep om er zeker van te zijn dat deze van de buurman was.

Laten we nu kijken naar een rand van een niet-lege groep - een stoel naast de stoel van een vaste persoon of de rand van de rij. Aangezien de stoel slechts één buur binnen de groep heeft, heeft de persoon die oorspronkelijk op deze stoel zat voordat de ruil plaats vond, slechts één optie waar te zitten. Evenzo heeft de persoon die aan de rand van de groep zit nadat de ruil een plaats heeft ingenomen, maar één optie waar hij eerder had kunnen zitten. Dit betekent echter dat het genoemde koppel van plaats verwisseld heeft, waardoor er een nieuwe "edge" ontstond. Daarom kunnen we in een groep mensen koppelen die gewoon van stoel moeten wisselen. Dit betekent dat elke groep een even aantal leden moet hebben om ze allemaal in overeenstemming met de probleemstelling te kunnen plaatsen.

We kunnen vervolgens elk van deze twee "samenvoegen" tot één persoon, waardoor $4$ "samengevoegde personen" ontstaan. De vraag blijft nu, op hoeveel manieren kunnen we de vaste personen daartussen plaatsen? Met de twee vaste personen hebben we $6$ posities om een persoon op te plaatsen. Daarom kunnen we de eerste vaste persoon op $6$ manieren plaatsen en de andere vaste persoon vervolgens op $5$ manieren, waardoor we $6\cdot 5=30$ opties krijgen. Maar tot nu toe hebben we elke optie twee keer geteld, want als we de twee vaste personen verwisselen, krijgen we geen nieuwe optie. Dit betekent dat de mensen op $15$ verschillende manieren van stoel hadden kunnen wisselen.

Antwoord:

$2$ $N∕\mathrm{cm}$

Als we de verbonden veren met een kracht $F$ uitrekken, worden beide veren met deze kracht uitgerekt. De veer met veerconstante $k_1=3N∕\mathrm{cm}$ verlengt met $\frac{F}{k_1}$. Evenzo wordt de veer met veerconstante $k_2=6N∕\mathrm{cm}$ langer met $\frac{F}{k_2}$. Als we de onbekende veerconstante van verbonden veren aanduiden als $k$, dan moeten de verbonden veren met $\frac{F}{k}$ verlengen. Daarom moet gelden dat:

Dus de verbonden veren hebben een veerconstante:

Antwoord:

$100$

Nadat Jaro $n$ zetten heeft uitgevoerd, wordt het fiche met $2+4+6+\cdots +2n$ tegels verplaatst. Als we nummer twee weghalen en een uitdrukking gebruiken voor de som van de eerste $n$ positieve gehele getallen, krijgen we: $2+4+6+\cdots +2n=2\cdot (1+2+3+\cdots +n)=2\cdot \frac{n(n+1)}{2}=n(n+1)$ Om het fiche te krijgen na het verplaatsen van $n(n+1)$ tegels op de tegel waar het begon, moet het getal $n(n+1)$ deelbaar zijn door $2020$. De priemfactorisatie van het getal $2020$ is $2020=2\cdot 2\cdot 5\cdot 101$. Dus speciaal het getal $n(n+1)$ moet deelbaar zijn door het priemgetal $101$. Het minste $n$ waarvoor het gebeurt is $n=100$ wanneer $n+1=101$. In dat geval is ook $n=100$ een factor $2\cdot 2\cdot 5=20$. Dus voor $n=100$ is het getal $n(n+1)$ deelbaar door $2020$. We hebben dus aangetoond dat na $100$ zetten de fiche op de begintegel komt en dat dit niet gebeurt na minder zetten. Daarom voert Jaro minimaal $100$ zetten uit.

Antwoord:

$10$ $\mathrm{cm}$

De enige externe kracht die op elke bal inwerkt, is de zwaartekracht en de normaalkracht van het oppervlak, die allemaal in verticale richting werken. Daarom kan het zwaartepunt van het systeem niet in horizontale richting bewegen. Wanneer het systeem stopt met bewegen, moet het zwaartepunt van het systeem zich boven het contactpunt van de grotere bal en het oppervlak bevinden. We hoeven alleen uit te zoeken hoe ver in horizontale richting van het oorspronkelijke contactpunt het massamiddelpunt van het systeem zich vóór de beweging bevindt. Het zwaartepunt van de grotere bal ligt boven het middelpunt met een afstand van $0$ $\mathrm{cm}$ in horizontale richting. Het zwaartepunt van de kleinere bal ligt echter op een afstand van $20$ $\mathrm{cm}$ in horizontale richting. Omdat de ballen een gelijke massa hebben, bevindt het massamiddelpunt van het systeem zich in het middelpunt van het lijnsegment dat de massamiddelpunten van de ballen verbindt. Dit betekent dat het oorspronkelijke zwaartepunt van het systeem zich op een afstand van $10$ $\mathrm{cm}$ horizontaal van het oorspronkelijke contactpunt met het oppervlak bevindt. De grotere bal beweegt daarom $10$ $\mathrm{cm}$ vanaf zijn oorspronkelijke contactpunt met het oppervlak.

Antwoord:

$22$

Bob trekt met kracht aan het touw $F=800N$. De spanning in het touw is dus gelijk aan de kracht $F$ in elk punt. Dit geldt ook voor de onderste katrol, aan beide zijden van het touw rond de onderste katrol. Daarom werkt het touw met een kracht van $2F$ en beweegt het omhoog. Dit geldt natuurlijk voor elke keer dat het touw om de onderste katrol gaat. Als het touw om de katrol $n$ keer draait, is de werkende kracht op de onderste katrol $2\mathit{nF}$. Om Scoop met zijn massa $m=3500\mathrm{kg}$ op te tillen, moet deze kracht groter zijn dan de zwaartekracht die op Scoop werkt. Daarom

En we kunnen zien dat het touw minstens $22$ keer om de onderste katrol moet gaan.

Antwoord:

$3$ $\mathrm{cm}$

Geef met $r$ de lengte van de straal van de kleinere cirkel aan. Als we een figuur tekenen, kunnen we enkele van de lengtes opschrijven:

Focus op het gemarkeerde rechter trapezium. De bases zijn stralen van de grotere en de kleinere cirkel. Het been dat loodrecht op de basis staat, heeft ook de lengte als de straal van de grotere cirkel. Ten slotte heeft het laatste been de lengte die de som is van de lengtes van de stralen van een kleinere en grotere cirkel. Verdeel dit trapezium over een rechthoek en een rechthoekige driehoek. In de rechthoekige driehoek staan de lengtes van de zijden $12$ $\mathrm{cm}$, $12\mathrm{cm}-r$, $12\mathrm{cm}+r$. Deze driehoek is juist, dus de stelling van Pythagoras geeft:

Dit betekent dat de straal van de kleinere cirkel $r=3\mathrm{cm}$ lang is.

Antwoord:

$39$ $\mathrm{mm}$

Wanneer Lucy de kiezelsteen of het marmer in een kubus bevriest, verandert ze het volume niet, maar verhoogt ze de massa. Dit verandert de gemiddelde dichtheid van de kubus. Als de kubus niet zinkt, is het volume van het onderwatergedeelte van de kubus recht evenredig met de gemiddelde dichtheid, daarom moet ook de hoogte van het onderwatergedeelte recht evenredig zijn met de gemiddelde dichtheid. Bovendien verhoogt het toevoegen van de kiezelsteen (of het marmer) altijd de gemiddelde dichtheid met dezelfde waarde. Dit verhoogt dus altijd de hoogte van het onderwaterdeel van de kubus met dezelfde waarde, wat ook betekent dat het altijd de hoogte van het deel boven het wateroppervlak met dezelfde waarde verlaagt.

Toen we in een kubus alleen de kiezelsteen hadden en we voegden het marmer toe, nam de hoogte van het deel boven water af met $3,2\mathrm{mm}-1,9\mathrm{mm}=1,3\mathrm{mm}$. Vandaar dat het toevoegen van het marmer altijd de hoogte van het deel boven water verlaagt met $1,3$ $\mathrm{mm}$. Als we de kubus met alleen het marmer zouden nemen en het marmer zouden weghalen, zou de kubus met alleen ijs de hoogte hebben van het deel boven water $2,6\mathrm{mm}+1,3\mathrm{mm}=3,9\mathrm{mm}$.

Voor een kubus met zijdelengte $a$, volume van het onderwatergedeelte $V^{\prime }$ en hoogte van het gedeelte boven water $h=3,9\mathrm{mm}$ halen we bovendien uit het principe van Archimedes dat:

Daarom had de kubus van Lucy een zijdelingse lengte $39\mathrm{mm}$.

Antwoord:

$24$

Het lijkt erop dat er geen patroon is in de eerste cijfers van de nummers in de eerste lijst. Het omgekeerde is echter de waarheid. Als we enkele van de eerste nummers in de tweede lijst noteren, valt het ons misschien op dat het nummer $1$ daar verdacht vaak voorkomt. Van daaruit nemen de aantallen toe totdat ze weer terugkomen op nummer $1$.

Laten we ons concentreren op de informatie, welke nummers elk vast nummer kunnen volgen:

• Het nummer $1$ mag alleen worden gevolgd door nummers $2$ of $3$.
• Het nummer $2$ mag alleen worden gevolgd door nummers $4$ of $5$.
• Het nummer $3$ mag alleen worden gevolgd door nummers $6$ of $7$.
• Het nummer $4$ mag alleen worden gevolgd door nummers $8$ of $9$.
• De nummers $5$, $6$, $7$, $8$ en $9$ mogen alleen worden gevolgd door nummer $1$ omdat een tien wordt overgedragen.

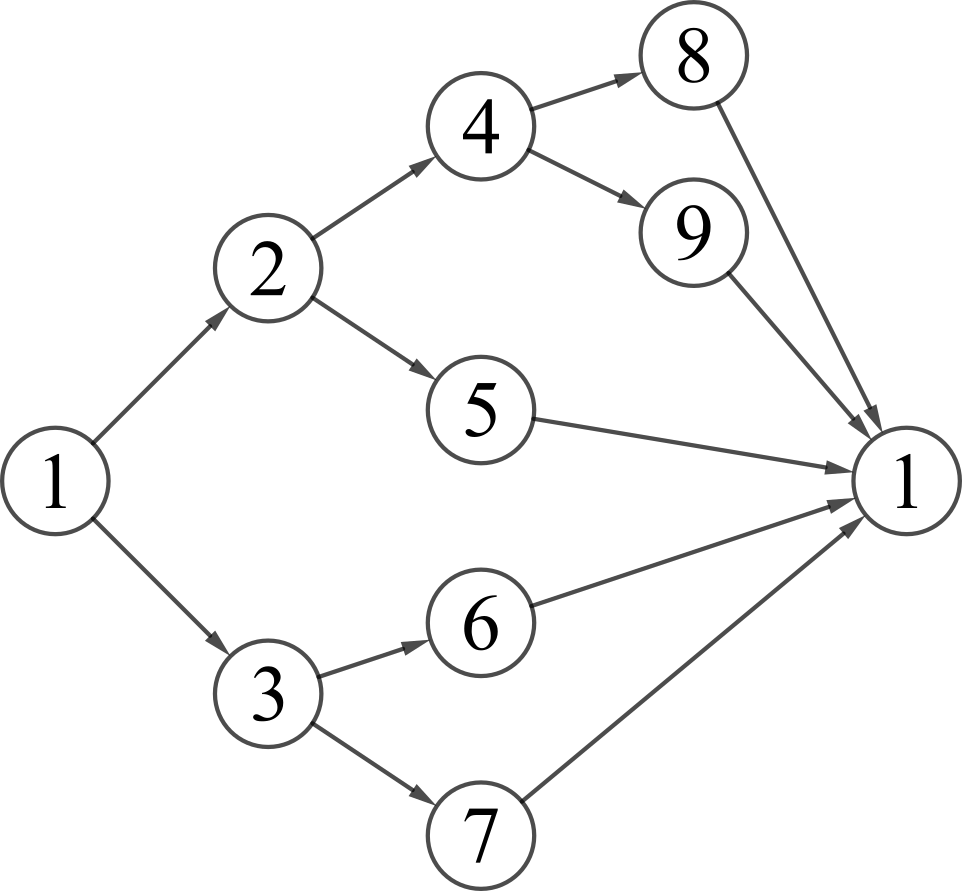
De mogelijke volgers van de getallen zijn in deze figuur getekend:

Hier kunnen we zien dat degenen de nummers in de tweede lijst in blokken verdelen. Bovendien zullen bijna alle blokken worden gevormd door exact $3$ getallen (inclusief nummer $1$). Er zijn slechts twee blokken die $4$ nummers bevatten - blok $1$, $2$, $4$, $8$ en blok $1$, $2$, $4$, $9$. Bovendien zijn dit de enige blokken die de nummers $8$ en $9$ bevatten.

We moeten ons nog één ding realiseren. Wanneer we een nummer $1$ in de tweede lijst bereiken, dan zal het respectieve nummer in de eerste lijst één cijfer meer hebben dan het nummer ervoor in de eerste lijst - dit komt omdat het nummer $1$ als eerste cijfer na het dragen van een tien.

Nu brengen we alles samen. We weten dat de laatste drie cijfers in de tweede lijst $1$, $2$, $5$ zijn, dus we slagen erin om het hele blok te voltooien. Met de nummers in het eerste blok kwamen de eencijferige nummers in de eerste lijst overeen en met het laatste blok kwamen de $167$-cijferige nummers in de eerste lijst overeen. Er moeten dus $167$ blokken zijn. Als ze allemaal uit $3$ getallen zouden bestaan, zouden ze in totaal $3\cdot 167=501$ getallen hebben. Dus $4$ getallen moeten in $555-501=54$ blokken staan. Dus $54$ keer moeten enkele van de getallen $8$ of $9$ in de tweede lijst voorkomen. Aangezien het getal $8$ $30$ keer voorkomt, moet het getal $9$ $54-30=24$ keer voorkomen.