Zadání a řešení úloh

Výsledek:

V roku 2012 byla výška jabloně . Během každého z následujících desíti roků vyrostla jabloň o . V roce 2022 má proto jabloň výšku .

Výsledek:

Stačí nám spočítat, po kolika stranách čtverce Anička prošla. Lehce spočítáme, že prošla po stranách, což odpovídá vzdálenosti .

Výsledek:

Janova průměrná rychlost je rovna podílu dráhy, kterou Jan uběhl, a času, za který tuto dráhu uběhl. Z grafu můžeme vyčíst, že Jan uběhl dráhu za , takže jeho průměrná rychlost byla .

Výsledek:

Jako první musíme vzít písmeno N. Když vezmeme písmeno N o dvě políčka doprava od počátečního políčka žetonu, tak dále musíme pokračovat písmenem A vpravo dolů od tohoto písmena N. Z něho už ale pohyby doprava a dolů nemůžeme vzít žádné písmeno B. To znamená, že musíme jako první vzít písmeno N pod políčkem, ve kterém začíná žeton.

Kdybychom dále chtěli vzít písmeno A o tři políčka doprava, dostali bychom se do stejného problému s písmenem B jako v předešlém úseku. jako druhé tak vezmeme písmeno A pod písmenem N.

Když budeme pokračovat písmenem B v levém dolním rohu, tak se do políčka s písmenem J můžeme dostat jen jedním způsobem. Když během toho projdeme také přes písmeno O, tak tímto dostáváme jednu možnost posouvání žetonu.

Jestli budeme pokračovat písmenem B ve třetím řádku a třetím sloupci, tak opět dostaneme dvě možnosti, jak pokračovat k písmenu O. V případě, že si vybereme písmeno O ve spodním řádku, tak do písmena J budeme moct přejít jediným způsobem. Když však půjdeme do druhého O, tak získáme tři možnosti.

Všechny možnosti, přesouvání žetonů jsou zobrazené na následujícím obrázku:

Dohromady má Dušan možností na přesouvání žetonů.

Výsledek:

Vyjadřujme se o směrech jako na obrázku. Paprsek se od pravé stěny na obrázku odrazí tak, že trefí levou stěnu o další metr směrem nahoru. To znamená, že levou stěnu trefí o metry nad místem, ze kterého byl paprsek vyslán. Od levé stěny se potom odrazí tak, že pravou stranu trefí o další metr výše, takže se trefí přesně do rohu s balónkem. Dráhu paprsku je možné vidět také na následujícím obrázku:

Dohromady se paprsek od stěny odrazí -krát.

Výsledek:

Laura ujede za jednu hodinu kilometrů. Jestli kilometry jsou doškoly, tak Laura ujede za hodinu doškoly. Jedna školohodina však trvá hodiny. Jestli Laura dokáže jet doškoly za hodinu, tak za tři čtvrtě hodiny (t.j. za jednu školohodinu) ujede doškoly. Laura tak dokáže jezdit na kole rychlostí doškoly za školohodinu.

Výsledek:

Rozdělme případy podle hodnoty první cifry. Jediné číslo, které začíná nulou, je číslo . To ale není kladné, takže podle Alexe není sestupné. Jestli je první cifra , tak za ní může následovat cifra nebo tam být nemusí. To dává možnosti a . Jestli je první cifra , tak za ní můžou následovat cifry a . To dává možnosti , , a . Celkem tak existuje sestupných čísel.

Výsledek:

Petr běžel na trase dlouhé rychlostí . To znamená, že celou trasu uběhl za .

Marek jel na kole rychlostí , takže ujet mu trvalo . Když dal Petrovi náskok minut, tak do cíle dorazil po tom, co Petr vyrazil.

Marek tak přijel do cíle dříve.

Výsledek:

Mohla se v číslech sedadel vyskytnout některá z cifer , , , , nebo ? Pokud by se tak stalo, bylo by příslušné číslo násobkem dvojky nebo pětky, nebo bychom dostali násobek dvojky nebo pětky po záměně cifer. Hledané čísla sedadel tak nemohou obsahovat žádnou z těchto cifer. Proto budou obsahovat pouze cifry , , nebo . To splňuje pouze čísel:

Z těchto čísel nejsou prvočísla čísla , , , , a . Tato čísla tak musíme vyloučit. Stejně musíme vyloučit číslo , kterému když vyměníme cifry, tak dostaneme složené číslo . Zůstanou tak už jen čísla:

Mário proto mohl objednat nejvýše lístků.

Výsledek:

Z Pythagorovy věty dokážeme vypočítat vzdálenost, kterou dítě projede při sklouznutí se po skluzavce. Tato vzdálenost je . Ze zadání víme, že sklouznutí trvá . Průměrná rychlost dítěte tak bude .

Výsledek:

Rozdělit obdélník na dva menší obdélníky jde pouze pomocí úsečky rovnoběžné s některou ze stran velkého obdélníku. V takovém případě bude mít tato úsečka stejnou délku jako ta strana, se kterou je rovnoběžná.

Zadání nám tedy říká, že máme obdélník s obvodem , jehož jedna strana má délku . Druhá strana tak musí mít takovou délku , že platí . Z toho vypočítáme .

Použitím úvahy ze začátku tohoto řešení máme, že strana s délkou musí mít stejnou délku jako cestička v druhém způsobu rozdělení obdélníku na dva stejné. V druhém způsobu by tak měla cestička délku .

Výsledek:

Použijeme zákon akce a reakce. Ten říká, že jestli nějaké těleso působí na jiné těleso nějakou silou , tak také těleso působí na těleso stejně velkou silou, ale opačného směru. V situaci z naší úlohy přitahuje Země Matouše gravitační silou s velikostí . Matouš tedy musí působit na Zemi stejně velkou gravitační silou, tedy silou s velikostí .

Výsledek:

Označme dráhu, kterou Sebinka ujela. Kdyby nezastavovala, tak by jí trvalo ujet tuto dráhu . Jestli však Sebinka zastavila na minut, tak tuto dráhu ujela za . Právě kvůli tomuto zastavení byla Sebinčina průměrná rychlost pouze . To vede k rovnici: Z toho vyplývá, že Sebinka ujela .

Výsledek:

U úloh se musel zmýlit někdo, kdo dal největší nebo nejmenší tip. Jestli to byl ten s nejmenším tipem, tak skutečný počet správně vyřešených úloh musel být buď , nebo . První možnost nevyhovuje, protože v takovém případě by se všichni ostatní zmýlili o víc než úloh. V druhé možnosti se zase ostatní lidé zmýlili u , a úloh, což nejsou rozdíly ze zadání.

O úloh se proto musel zmýlit ten člen týmu, který si tipl . Z podobného důvodu jako v předešlém případě nemůže být počet správně vyřešených úloh , ale . V tomto případě dostáváme, že zbylí členové se zmýlili o , a úlohy. To jsou rozdíly shodné se zadáním.

Tým tedy správně vyřešil úloh.

Výsledek:

Zamysleme se co znamená, když někdo o někom říká, že (není) je špión. Například Alice tvrdí, že Dan je špión. Pokud Alice říká pravdu (tedy ona není špión), tak je Dan špión. Jestli Alice neříká pravdu (tedy ona je špión), tak Dan není špión. To znamená, že Alice a Dan jsou na opačných stranách - jeden z nich je špión a druhý ne.

Ještě se podívejme například na Baščino tvrzení. Jestli Baška říká pravdu (tedy ona není špión), tak Cyril také není špión. Ale jestli Baška neříká pravdu (tedy ona je špión), tak Cyril je také špión. To znamená, že Baška a Cyril jsou na stejných stranách - buď ani jeden z nich není špión, nebo jsou oba špióni.

Podle tvrzení, která zazněla, jsou Baška a Cyril na stejných stranách. Také Dan a Erik jsou na stejných stranách. Pokud by byla Alice špiónem, tak by kromě ní musela být jedna z dvojic Baška a Cyril, nebo Dan a Erik dvojicí obsahující dva špióny. V takovém případě bychom měli alespoň tři špióny, což je problém. Tím pádem Alice není špión. O Danovi ale tvrdí, že je špión, takže Dan musí být špión. Ten je na stejné straně jako Erik, který proto musí být také špión. Zbylí dva, Baška a Cyril, špióny nejsou.

Takže špióni jsou Dan a Erik, jejichž součet čísel je .

Výsledek:

Označme hledanou velikost Petrova souboru. Jestli Petr nahraje soubor bez komprese, potrvá to . Jestli se však Petr rozhodne zkomprimovat soubor, tak komprese bude trvat . Od tohoto momentu bude mít soubor velikost . Po sekundách ho Petr začne nahrávat do úložiště a nahrávání bude trvat . Takže v případě komprese to Petrovi potrvá . Tento čas se podle zadání rovná času bez komprese. To vede k rovnici, kterou vyřešíme následujícím způsobem: Vypočítali jsme, že velikost Petrova souboru je .

Výsledek:

Všimněme si, že obvod celé zahrady se rovná součtu obvodů částí s obvody , a části s otazníkem. To proto, že některé strany těchto tří častí můžeme přesunout na obvod celé zahrady a dostaneme tím celý obvod zahrady:

Z toho vyplývá, že obvod části označené otazníkem je .

Výsledek:

Čím větší bude vzdálenost, na které bude Adrian brzdit, tím menší sílu bude potřebovat. Předpokládejme proto, že auto zabrzdí na dráze . Aby auto brzdilo, musí na úkor své energie, v tomto případě kinetické, konat práci na překonání brzdné síly. Auto zastaví, když spotřebuje všechnu kinetickou energii.

Kinetická energie auta s hmotností a rychlostí je . Takovou práci musí vykonat síla s velikostí , kterou auto překonává brzdnou sílu se stejnou velikostí. Na dráze tato síla vykoná práci . To vede na vztah: Na auto tedy musí působit brzdná síla s velikostí alespoň:

Výsledek:

Sumu nedokážeme zaplatit žádným možným způsobem. Můžeme totiž použít buď nebo minci s hodnotou - když bychom použili víc, překročili bychom sumu . V obou případech ale nemůžeme zbytek sumy zaplatit pouze mincemi v hodnotě . Zároveň dokážeme zaplatit všechny větší sumy než . Začneme s (), () a (). Když dokážeme zaplatit tyto tři sumy, tak dokážeme už zaplatit také libovolnou větší sumu - stačí k těmto sumám přidávat mince s hodnotou .

Proto je největší suma, kterou Klára nemůže zaplatit bez toho, aby jí prodavač vrátil, suma .

Výsledek:

Celá situace je osově souměrná podle osy úsečky, která spojuje obě kuličky. To zůstane i po nárazu, když se kuličky spojí do větší masy. Pokud by se tahle masa pohybovala doleva nebo doprava, tak by situace už nebyla symetrická. Výsledná plastelínová masa tak zůstane po nárazu stát.

Při nárazu každá z kuliček ztratí svoji kinetickou energii, která se podle předpokladu ze zadání přemění na teplo. To se potom dodá mase, která se tím ohřeje.

Každá z kuliček (s hmotností a rychlostí ) má kinetickou energii . Spolu tak mají kinetickou energii . Tato energie se ve formě tepla dodá plastelínové mase. Ta má hmotnost (jsou v ní obě kuličky s hmotností ), měrnou tepelnou kapacitu a její teplota se změní o . Proto platí: Jestli byla teplota kuliček před srážkou , tak teplota masy po srážce bude:

Výsledek:

Aby byla Houpačka v rovnováze, musí se rovnat momenty sil působící na obou stranách houpačky. Danka, s hmotností , sedí ve vzdálenosti od osy otáčení. Na Danku tak působí tíhová síla . Danka tak na houpačku působí stejně velkou tíhovou silou a ta působí na houpačku momentem: Stejně velkým momentem musí působit kostky na opačné straně. Předpokládejme, že těchto kostek je . Ze zadání mají hmotnost a stranu dlouhou . Spolu mají hmotnost a tvoří kvádr dlouhý . Jeho těžiště se nachází ve vzdálenosti od osy otáčení, takže takhle dlouhé je také rameno tíhové síly působící na kostky brané jako jeden velký kvádr. Moment síly, kterým působí kvádr na houpačku, je potom: Dosazením těchto momentů do rovnosti dostáváme: Počet kostek, které Ninka musela položit, je proto:

Výsledek:

Zamysleme se, které cifry mohou být na místě jednotek. Nemohou tam být cifry , a , protože by dané číslo bylo násobkem a tím pádem by nebylo prvočíslem. Podobně je problém také s cifrou , pro kterou by bylo vzniklé dvojciferné číslo násobkem . Tak můžeme určit, že cifry , , a budou na místě desítek a zbylé cifry , , a na místě jednotek. Jediný, a tedy také maximální, možný součet všech čtyř prvočísel proto musí být .

Poznámka: Kartičky se také opravdu dají rozdělit tak, abychom dostali dvojciferná prvočísla. Například takhle: , , , .

Výsledek:

Dvě přímky v rovině, které se neprotínají, jsou rovnoběžné. Hledáme tedy počet dvojic rovnoběžných přímek, které jsou určené sedmi vyznačenými body.

Označme vyznačené body postupně , , , , , a . Hledejme všechny přímky určené těmito body, které jsou rovnoběžné s přímkou . To jsou přímky a . Je to proto, že pravidelný sedmiúhelník je symetrický podle osy úsečky . Přímky , a jsou z této symetrie kolmé na osu úsečky , a tedy navzájem rovnoběžné. Tímto dostáváme první dvojice rovnoběžných přímek.

když podobnou úvahu zopakujeme také pro přímky , , , , a , dostaneme pokaždé dvojice rovnoběžných přímek.

Každou z přímek určených body až tímto určíme jako rovnoběžnou s některou z přímek , , , , , a (těchto přímek je navzájem rovnoběžných). Tím dostáváme všechny dvojice rovnoběžných přímek.

Celkem tedy může Tete nakreslit dvojici přímek způsoby.

Výsledek:

Při vyhození míčku má míček potenciální energii , kde je jeho hmotnost, je výška, ze které Serena vyhodila míček, a je tíhové zrychlení. Když označíme , tak kinetická energie míčku při vyhození je . Během celého pohybu se zachovává celková energie míčku. Tedy součet je v každém momentě stejný. Například také v momentě těsně před dopadem. Zde se míček nachází v nulové výšce, takže jeho potenciální energie je nulová. Celá energie se tak v tomto momentě bude rovnat kinetické energii. Jestli si označíme rychlost míčku těsně před dopadem, tak dostáváme rovnost: Rychlost míčku těsně před dopadem je tedy:

Výsledek:

Jediné jednociferné číslo, které se rovná -násobku svého ciferného součtu, je číslo . I kdybychom nulu brali mezi přirozené čísla (v některých částech matematiky se bere nula jako přirozené číslo, v některých ne), tak by to nezměnilo součet čísel, která Jonáš našel.

Pokud by Jonáš našel nějaké vyhovující dvojciferné číslo, tak bychom si ho mohli napsat ve tvaru , kde a jsou jeho cifry. Avšak -násobek ciferného součtu tohoto čísla je a platí . Třináctinásobek ciferného součtu dvojciferného čísla tak nikdy nebude rovný tomuto číslu.

Pokračujme s trojcifernými čísly, přičemž každé z nich si můžeme zapsat ve tvaru . Jestli je toto číslo trojciferné, tak . Podmínka s ciferným součtem vede ke vztahu: Když , tak pro cifry a dostáváme tři možnosti. Hodnoty jsou v nich , a , což odpovídá číslům , a . Jiné možnosti pro nemáme, jestli , pro bychom tak dostali a zároveň o pravé straně víme, že . V dalších možnostech by tedy nemohla platit rovnost . Tím jsme vyřešili případ trojciferného čísla.

Čtyřciferné číslo má ciferný součet nejvýše , takže -násobek ciferného součtu bude určitě menší, než (samozřejmě, mohli bychom také spočítat, kolik je , ale na vytvoření následujícího závěru nám stačí takovýto hrubý odhad). Můžeme tak říct, že -násobek ciferného součtu určitě nebude čtyřciferné číslo. Jonáš proto nemohl najít žádné čtyřciferné číslo. Ze stejného důvodu Jonáš nemohl najít ani žádné číslo s větším počtem cifer.

Jonáš tedy našel čísla se součtem .

Výsledek:

Čtverec má obě svoje úhlopříčky stejně dlouhé a navzájem kolmé. Víme, že úhlopříčka celé značky je dlouhá . Každá z úhlopříček rozděluje celý Čtverec na dva trojúhelníky, jejichž výška je tvořena polovinou druhé úhlopříčky. Takový trojúhelník tak má obsah . Celá značka, skládající se ze dvou takových trojúhelníků, má proto obsah = .

Žlutá část zabírá celé značky, takže má obsah . Její strana je proto dlouhá .

Výsledek:

Nechť má pás délku . Z případu, když Jerry stojí pouze na páse, můžeme zjistit jeho rychlost. Jestli se v tomto případě Jerry doveze na konec pásu za čas , tak je rychlost pásu . Podobně v případě, když Jerry kráčí podél pásu, můžeme určit rychlost Jerry. Když jí to trvá , tak má rychlost .

Když Jerry kráčí proti směru pohybu pásu, tak její rychlost je , a proto Jerry trvá přejít pás: V případě, kdy Jerry kráčí ve směru pásu, je její rychlost . Na konec pásu tedy přejde za čas: Z toho dokážeme zjistit, že když bude Jerry kráčet proti směru pohybu pásu, bude jí to trvat déle o čas:

Výsledek:

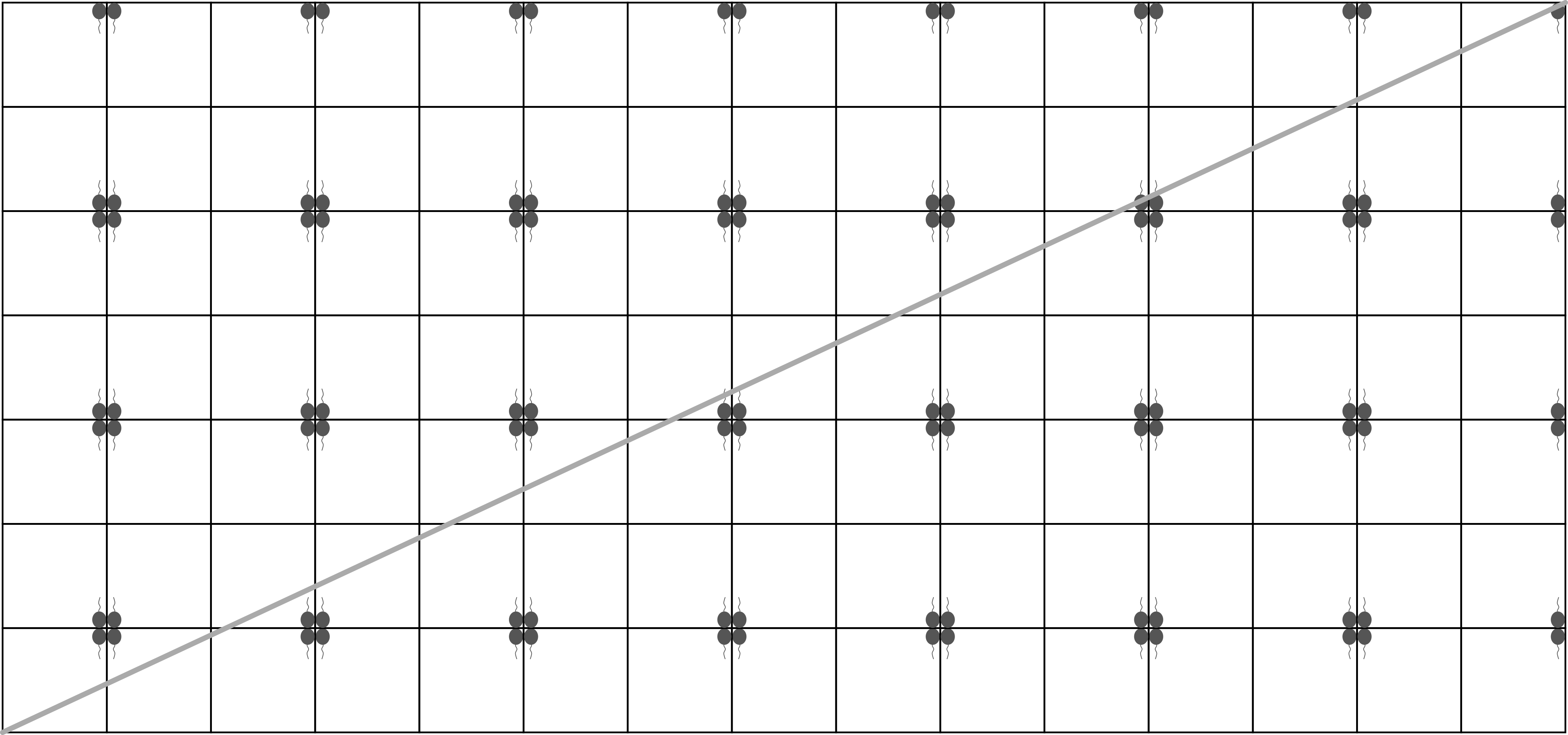
Pochopme nejprve, jak vypadají množiny a .

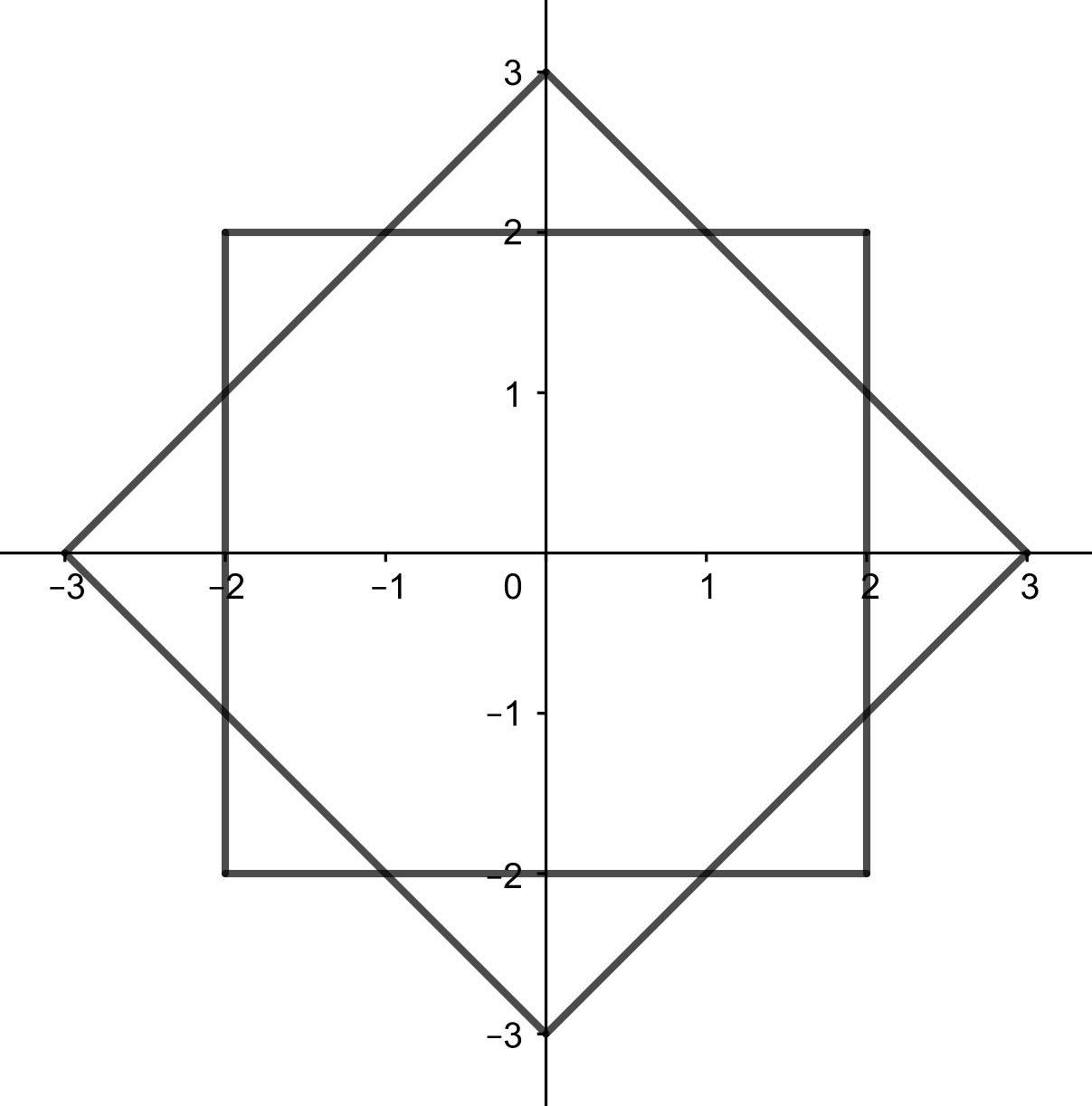
Funkce , nazývaná také absolutní hodnota, udává vzdálenost čísla od nuly. Možná to tak na první pohled z definice uvedené v poznámce není vidět, ale absolutní hodnota maže znamínko . Podívejme se na , jestli a . Když . Podmínka tedy dává , a tedy . To je nějaká přímka, na které leží body a . Vzhledem k podmínce a to je však pouze úsečka spojující tyto dva body. Pro ostatní případy znamének a dostáváme, že množinu tvoří úsečky spojující body a , body a , body a , body a . Toto je ve skutečnosti Čtverec s vrcholy v bodech , , a .

Pokračujme množinou . Ta je popsána vztahem . Tato Funkce, nazývaná maximum, má jako hodnotu větší z a . Aby se tato Funkce rovnala , tak některé z a musí být a to druhé musí být menší. Jestli , tak nebo . V tom případě má být , což znamená, že . Pro to splňují body na úsečce mezi body a . Pro to zas splňují body na úsečce spojující a . Když uděláme podobný rozbor pro , tak se do množiny přidá úsečka spojující a a úsečka spojující a . Množina tak bude také Čtverec, tentokrát s vrcholy , , a .

Množiny a jsou nakreslené na tomto obrázku:

Odtud vidíme, že čtverce odpovídající množinám a se protínají v bodech, takže bodů, které leží současně v aj je .

Výsledek:

Předpokládejme, že v pravé větvi je rezistorů a v levé větvi rezistorů. Potřebujeme najít hodnotu . Odpor sériově zapojených rezistorů v pravé větvi je , kde je odpor jednoho rezistoru. Odpor rezistorů v levé větvi je zase . Odpor celého zapojení je potom: Podle zadání je ale tento odpor -krát menší, než odpor v v pravé větvi. Odtud dostáváme rovnost, které úpravou získáme hodnotu : V pravé větvi je tedy zapojeno -krát více rezistorů.

Výsledek:

Marianka bude konat práci na to, aby zvedla kámen s hmotností dostatečně vysoko na to, aby celý kámen přelezl přes zeď. Potřebujeme tak zjistit, do jaké nejmenší výšky musíme zvednout těžiště.

těžiště v trojúhelníku rozděluje těžnici na dvě části, kterých délky jsou v poměru , přičemž delší část těžnice je při vrcholu. V rovnostranném trojúhelníku je každá těžnice zároveň výškou, takže je těžnice dlouhá . těžiště je proto vzdálená od každé strany tohoto trojúhelníku . Proto je těžiště od každého bodu na některé straně trojúhelníku vzdálená aspoň .

V momentě, když bude těžiště trojúhelníku přesně nad zdí, tak nějaký bod na nějaké straně trojúhelníku se bude dotýkat vrchu zdi (když by to tak nebylo, tak bychom mohli celý trojúhelník posunout dolů a Marianka by vykonala menší práci). Tento bod je od těžiště vzdálený alespoň . Proto musíme při přenášení kamene nad zeď zvednout těžiště kamene alespoň nad vrch zdi. Z opačného pohledu kámen dokážeme opravdu přenést tak, abychom těžiště zvedli jen do výšky nad vrch zdi. Stačí přitom například udržovat jednu ze stran trojúhelníku vodorovně.

To znamená, že Marianka při přehazování kamenu nad zdí musí zvednout těžiště kamenu o , aby dostala těžiště do výšky vrchu zdi, a ještě o dalších . Celkem tedy zvedne těžiště o . přitom zvýší potenciální energii kamenu o . Marianka vykonala práci přesně na to, aby kamenu zvedla potenciální energii o , takže vykonala práci .

Výsledek:

Jestli si na začátku vybral Andrej čísla a , tak na tabuli budou také čísla a . Kdyby bylo některé z čísel a nulové, řekněme , tak by aritmetickou posloupnost musela v nějakém pořadí tvořit čísla , , , . Některá dvě po sobě jdoucí čísla této aritmetické posloupnosti musí být a , a tak se každé dvě po sobě jdoucí čísla této postupnosti liší o . Jinými slovy, všechna čísla v ní jsou stejná. Proto také . To ale nemůže nastat, protože a mají být různá.

Dále tedy můžeme předpokládat, že i jsou větší než . Také můžeme předpokládat, že (pokud by platila opačná nerovnost, tak jen přeměňujeme a ). V takovém případě dokážeme říct, že největší mezi čísly na tabuli je číslo a druhé největší je číslo . jestli v aritmetické postupnosti musí čísla postupně narůstat nebo klesat, tak a musí být dvě po sobě jdoucí čísla v této postupnosti. Dvě po sobě jdoucí čísla se tak musí lišit o .

Z tohoto vidíme, že třetí číslo v aritmetické postupnosti musí být číslo , neboť to musí být číslo o menší než . Poslední číslo potom bude , které má být o menší než . To dává podmínku: Opravdu když si na začátku Andrej vybere čísla a , tak připsáním jejich součtu a kladného rozdílu dostane aritmetickou posloupnost , , a .

Zbývá už pouze dořešit, kolik dvojic a je navíc takových, že i jsou jednociferná čísla. Lehce ověříme, že takové dvojice jsou jen , a . Andrej si tak mohl vybrat dvojici čísel způsoby.

Výsledek:

Když potáhneme lano, tak se volné kladky spolu se závažím vytáhnou o nějakou vzdálenost směrem nahoru. Přitom jakoby zmizí část lana, která z nich vychází, protože to je ta část lana, která prošla našima rukama. Na obrázku je vidět, co se stane, když se kladky zvednou z dolní čárkované čáry na horní čárkovanou čáru - ze všech pěti úseků lana mezi těmito dvěma čarami jakoby zmizí stejně dlouhý kus lana. To znamená, že když potáhneme lano o nějakou délku, tak se závaží spolu s volnými kladkami zvednou tak, aby mezi příslušnými čárkovanými čarami zmizelo přesně tolik lana, o kolik jsme lano potáhli. Takže závaží se vždy zvedne o pětinu toho, o kolik jsme potáhli lano. Jestli tedy taháme lano rychlostí , tak se závaží zvedá rychlostí .

Výsledek:

Připomeňme si, jak počítáme nejmenší společný násobek a největší společný dělitel dvojice čísel. Nejprve potřebujeme zjistit prvočíselný rozklad jednotlivých čísel. Potom pro každé prvočíslo uděláme to, že do nejmenšího společného násobku dáme toto prvočíslo tolikrát, kolikrát se nachází v tom čísle, kde se nachází vícekrát. Do největšího společného dělitele ho dáme tolikrát, kolikrát se nachází v tom čísle, kde se nachází méněkrát. Z toho, jak rozdělujeme tato prvočísla se dá vidět, že musí platit vztah pro libovolná dvě přirozená čísla , .

Vezměme si teď za , dvojici čísel, která splňují Tomášovi podmínky. Pro tato dvě čísla platí a . Dosazením do získaného vztahu dostáváme z předešlého úseku: Obě čísla i jsou proto násobkem , a tedy je můžeme napsat ve tvaru , pro nějaké přirozená čísla a . Zároveň se snažíme najít dvojici s maximálním součtem je stejné jako snažit se najít dvojici a s co největším .

Jestli největší společný dělitel čísel a byl , tak největší společný dělitel čísel a musí být . Taktéž víme, že: Dvě čísla s daným součinem mají největší součet, když se od sebe liší co nejvíce. Nejvíce se liší, když a (nebo naopak). V tomto případě také opravdu platí, že a tato dvě čísla dávají také největší možný součet . Po návratu k číslům , dostáváme, že součet Tomášových čísel je .

Výsledek:

Podívejme se, jak v této úloze působí síly. Na most, který váží , působí v jeho středu tíhová síla . Kromě toho na most působí síla ze řetězu. Aby se tento most nehýbal, tak nesmí ani rotovat. Nerotuje v moment, kdy se momenty sil působících na most navzájem vyruší. Tíhová síla působí ve vzdálenosti na most momentem síly . Svislá složka síly od řetězu působí ve vzdálenosti a musí působit momentem . Musí tak mít velikost . Každému řetězu z toho připadá poloviční síla, tedy síla .

Máme tedy složku síly napínající řetěz ve svislém směru. jak ale najít sílu ve směru řetězu? Všimněme si, že trojúhelník tvořený řetězem, bránou a mostem je podobný s trojúhelníkem tvořeným hledanou silou , silou a spojnicí jejich koncových bodů. Poměr velikostí a je proto stejný jako poměr výšky brány a délky řetězu. Délku řetězu dokážeme spočítat z Pythagorovy věty jako . Proto: Každý z řetězů je proto napínán silou:

Výsledek:

Nejprve hledejme pravděpodobnost, že počet jedniček je sudý. Nechť je prvních cifer úplně náhodných. Sudost počtu jedniček mezi nimi je nějaká. Poslední cifra je buď , nebo . Podle toho, jakou má hodnotu, má počet cifer v celém souboru buď stejnou, nebo opačnou paritu jako počet cifer mezi prvními ciframi. Obě situace však nastanou se stejnou pravděpodobností, a tak je počet jedniček v celém souboru sudý s pravděpodobností .

Dále se podívejme na to, jaká část možností, jak dostat sudý počet jedniček, obsahuje počet jedniček dělitelný čtyřmi. Když je v souboru sudý počet jedniček, tak mohou nastat dvě situace - buď je počet jedniček dělitelný čtyřmi, nebo jejich počet dává po dělení čtyřmi zbytek . Dejme do skupiny všechny možnosti s počtem jedniček dělitelným čtyřmi a do skupiny všechny možnosti s počtem jedniček dávajícím zbytek po dělení čtyřmi. Všimněme si následující věci. Vezměme si možnost ze skupiny a změňme všechny nuly na jedničky a všechny jedničky na nuly. Jestli v původní možnosti bylo jedniček a nul, tak po této záměně dostaneme možnost, ve které je jedniček a nul. Číslo dává zbytek po dělení čtyřmi. Tímto tedy můžeme změnit libovolnou možnost ze skupiny na možnost ze skupiny . Když opět změníme jedničky a nuly na nuly a jedničky, tak dostaneme opět původní možnost ze skupiny .

Takto rozdělíme možnosti na dvojice obsahující jednu možnost ze skupiny a jednu možnost ze skupiny . Každá možnost je z přesně jedné skupiny. Proto musí mít skupiny a stejnou velikost. To ale znamená, že pravděpodobnost, že v možnosti se sudým počtem jedniček je ve skutečnosti počet jedniček dělitelný čtyřmi, je .

proto je pravděpodobnost, že počet zaznačených jedniček je dělitelný čtyřmi, rovna .

Výsledek:

Když zkusíme několikrát odrazit paprsek, tak to vypadá, že netrefí balónek tak brzo. Navíc musíme pokaždé počítat, kde přesně se odrazí, což není až tak jednoduché a příjemné. Zkusme tedy něco jiného.

Zkusme namísto překlápění paprsku kolem kolmice na stěnu, do které paprsek narazil, překlápět samotnou místnost. Řekněme, že vedle pravé stěny se nachází přesně stejná místnost, akorát že překlopená podle pravé stěny původní místnosti. Kdybychom náš paprsek nechali projít skrz pravou stěnu, tak by v této zrcadlové místnosti svítil přesně stejně, jako by svítil odražený stěnou v původní místnosti. Opakováním takového překlápění můžeme předpokládat, že paprsek se pohybuje pouze přímo a překlápíme místnost.

Z informace o prvním odraze v původní situaci víme, že vždy, když se přímý paprsek posune na obrázku doprava o , tak se posune nahoru o . Po určitém čase se paprsek trefí přesně do rohu některé překlopené místnosti a s trochou štěstí to bude ten, ve kterém se nachází i balónek. Paprsek trefí nějaký roh, když bude jeho uražená vzdálenost doprava i nahoru nějakým násobkem délky . Když paprsek projde doprava, tak Podle první věty tohoto odstavce projde nahoru. Když je celé číslo, tak je násobkem délky , Hledáme tedy nejmenší celé číslo , pro které je násobkem . Jestli , tak nejmenší takové musí být . Situace poté dopadla tak jako na obrázku:

Z obrázku vidíme, že jsme opravdu trefili správný roh (ten, ve kterém je balónek). Jak ale spočítat počet odrazů od stěny? Odraz v našem předělání úlohy odpovídá tomu, že paprsek prošel do jiné místnosti. Z obrázku je vidět, že paprsek -krát prošel do místnosti vpravo a -krát do místnosti nahoře. Dohromady tedy prošel do jiné místnosti -krát, takže v původní formulaci úlohy se odrazil -krát.

Poznámka: Na tomto obrázku je možné vidět, jak přesně se paprsek -krát odrazil, než trefil balónek:

Výsledek:

Po přisypání mouky s hmotností do sklenice s podstavou s obsahem se tíhová síla působící na tuto sklenici zvýšila o . Na to, aby sklenice stále plavala, se musela vztlaková síla zvýšit o stejnou velikost. Vztlaková síla se mohla zvýšit jen tím, že se zvětšila ponořená část této sklenice. Pro tuto změnu máme z Archimedova zákona vztah , kde je změna objemu ponořené části. Odtud dostáváme: Aby se mohl zvětšit objem ponořené části, tak dno menší nádoby musí klesnout, a tedy se přiblížit ke dnu větší nádoby o nějakou výšku . Při tom mu v cestě jakoby zavazí válec vody s objemem , který se tak musí někam přesunout. Přesune se k boku menší sklenice. Tam způsobí nárůst hladiny vody ve větší sklenici o . Objem vody, který se sem přesunul, dokážeme vyjádřit také jako , kde je obsah podstavy větší sklenice. Tím získáváme vztah: Při těchto posunech se výška ponořené části menšího válce zvětší o a tedy jestli známe její objem, tak dostáváme také vztah: Zkombinováním obou získaných vztahů dostáváme: Takže hladina se ve větší sklenici zvedla o výšku:

Výsledek:

Spočítat takhle mnoho devítek by bylo velmi náročné. Hledejme proto jiný způsob, jak Zuzčina čísla sčítat. Všimněme si, že když každé číslo zvětšíme o , dostaneme číslo začínající jedničkou, za kterou následuje několik nul. Součet proto dokážeme zapsat jako . Když dáme všechny čísla dohromady, dostaneme . Ostatní čísla součtu vytvoří číslo , ve kterém se nachází jedniček. Zuzčiným výsledkem je toto velké číslo zmenšené o .

Jak toto číslo vypadá? Odečítání ovlivňuje jen posledních cifer velkého čísla, které se změní na . Zbylých jedniček zůstává neměnných. Ciferný součet Zuzčina výsledku je proto .

Výsledek:

Předpokládejme, že cihla má rozměry , , a hmotnost . Poté tlaky , a ze zadání dokážeme vypočítat jako: Když tyto tři vztahy navzájem vynásobíme, dostaneme: Jenže je objem cihly. Vztah tedy dokážeme upravit na tvar: Dále si potřebujeme už jen uvědomit, že podíl je hustota cihly . Z toho už dokážeme získat hmotnost cihly: Bobova cihla tedy měla hmotnost .

Výsledek:

Protněme přímky a . Jejich průsečík nazveme . Díky rovnoběžnosti a jsou trojúhelníky a podobné. Koeficient podobnosti těchto trojúhelníků je . Tato podobnost dává vztahy: Víme však, že a . Použitím těchto vztahů dostáváme: V trojúhelníku platí , takže Podle Pythagorovy věty je tento trojúhelník pravoúhlý s pravým úhlem při vrcholu . Takže také trojúhelník je pravoúhlý. Obsah lichoběžníku se rovná rozdílu obsahů těchto dvou trojúhelníků.

Trojúhelník má odvěsny dlouhé a , takže jeho obsah je . Trojúhelník má odvěsny dlouhé a , takže jeho obsah je . Lichobežník má proto obsah .

Výsledek:

Vyřešme nejprve jednodušší příklad, kdyby měla Tete na kružnici jen body. Označme si tyto body , , a tak, aby šly po kružnici v tomto pořadí. Nakreslené úsečky nesmí mít společné ani krajní body, takže jedna úsečka bude mít svoje krajní body v jedné dvojici bodů a druhá úsečka bude mít svoje krajní body v druhé dvojici vyznačených bodů. To znamená, že dvojici úseček můžeme nakreslit pouze třemi způsoby:

1. úsečky a ,

2. úsečky a ,

3. úsečky a .

V druhém případě se úsečky protínají, ve zbylých případech ne. V případě pro body tak máme možnosti jak nakreslit dvojici úseček.

Teď se můžeme vrátit k příkladu, ve kterém má Tete na kružnici bodů. Dvojice úseček bude mít krajní body v nějakých různých bodech. Když vybereme, které body to budou, tak budeme moci aplikovat příklad, ve kterém máme pouze body. Tím pádem budeme mít po výběru čtveřice bodů možnosti jak nakreslit úsečky.

Zbývá tedy spočítat, Kolika způsoby můžeme vybrat body. Na vybrání prvního z nich máme možností, na druhý možností, na třetí a na čtvrtý možností. Přitom jsme ale každou čtveřici započítali vícekrát. Konkrétně jsme ji započítali za každé možné zařazení těchto čtyř bodů. Na výběr prvního z těchto čtyř máme možnosti, na druhý , na třetí a na poslední možnost. Možností, jak vybrat body, je proto .

Spolu s tím, že pro každou čtveřici máme možnosti nakreslení dvojice úseček, dostáváme, že Tete může nakreslit úsečky způsoby.

Výsledek:

Označme si hmotnosti jednotlivých kvádrů jako , , a koeficient smykového tření . Podívejme se na síly, které působí na jednotlivé kvádry. Ty působí tak, jako na tomto obrázku:

Síly , a jsou tíhové síly působící na jednotlivé kvádry. Pokud kvádry na sebe navzájem tlačí, vznikají normálové síly a . Silou s velikostí působí horní kvádr na prostřední směrem dolů. Zároveň Podle zákonu akce a reakce tlačí stejně velkou silou, jen směrem nahoru, i prostřední kvádr na horní kvádr. podobně to platí také mezi prostředním a spodním kvádrem se silou o velikosti . Zároveň podložka tlačí na spodní kvádr normálovou silou .

Vodorovně působící síly jsou síla , kterou bude Majo působit na spodní kvádr, a síly a , které odpovídají napětí v laně. Nakonec posledními sílami jsou třecí síly. Na vrchní kvádr, který by se chtěl pohybovat doprava, působí směrem doleva třecí síla . Opět ze zákona akce a reakce musí působit i na prostřední kvádr síla s velikostí , ale směrem doprava. Podobně působí také třecí síly mezi prostředním a spodním kvádrem. Také podložka působí na spodní kvádr třecí silou .

Aby se žádný kvádr nehýbal, musí být součet sil působících na ně nulový, a to v každém směru. Ve svislém směru to dává rovnice: Ve vodorovném směru zase rovnice: Tíhové síly vypočítáme jednoduše ze vztahu , kde je tíhové zrychlení. Když bude Majo působit maximální možnou silou, tak i třecí síly budou maximální možné - v té chvíli totiž platí, že když by Majo působil o trochu větší silou, celá soustava by se hýbala a třecí síly by působily maximální možnou velikostí. Jejich velikosti tak vypočítáme pomocí vztahu . Už stačí jen postupně vyjadřovat neznámé velikosti ze šesti rovnic výše, čímž dostaneme: Největší síla, kterou může Majo působit, má tedy velikost: