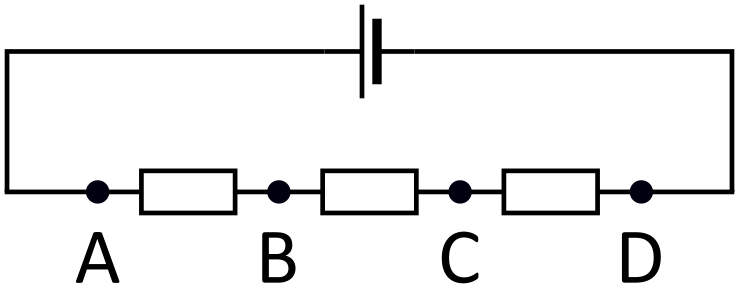
Výsledek:
Napětí mezi dvěma body popisuje velikost rozdílu potenciálů v těchto dvou bodech. Potenciál vyjadřuje pouze (elektrickou) potenciální energii částice s nábojem . V každém z bodů , , a by tato částice měla určitou potenciální energii. Takové číslo můžeme přiřadit každému z bodů. Napětí potom pouze popisuje rozdíly mezi těmito čísly.
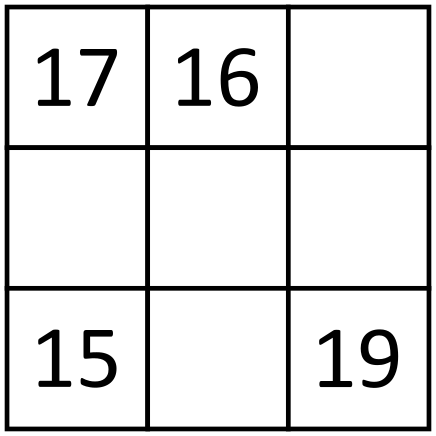
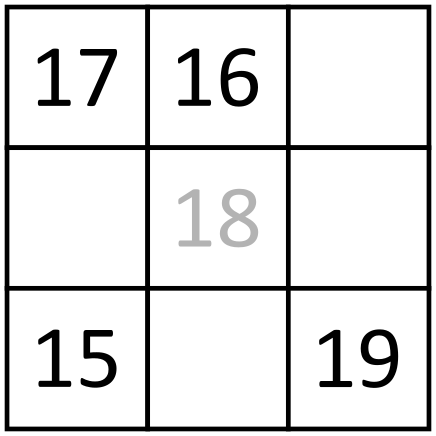
Můžeme tedy reformulovat úlohu na přiřazení čtyř čísel k , , a (tato písmena nyní nemají nic společného s písmeny v původním zadání), tak, aby jejich rozdíly byly , , , , a poslední neznámý. Všimněme si jedné zajímavé vlastnosti. Vezmeme 3 z našich čísel, řekněme , a , a uspořádejme je tak, že . Potom rozdíl je součet rozdílů a (zřejmě ). Pokud tedy vezmeme libovolná čísla, pak rozdíl mezi nimi bude mít tu vlastnost, že jedno bude součtem zbylých dvou.
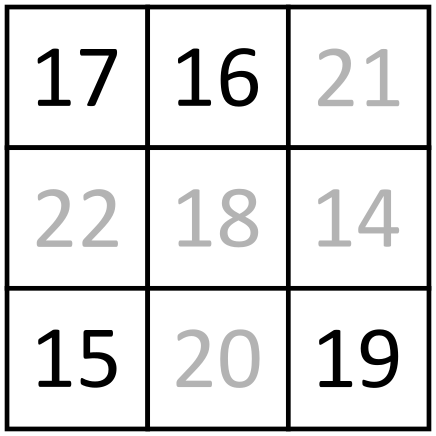
Nyní se vraťme zpět k našemu problému. Řekněme, že náš neznámý rozdíl je rozdíl mezi a . Vezměme čísla , a . Všechny rozdíly mezi nimi jsou mezi známými. Protože jeden z nich musí být součet zbylých dvou, máme pouze dvě možnosti: nebo . Obdobná vlastnost musí platit i pro trojici , a , takže jedna z trojic bude mít rozdíly , a a druhá bude mít rozdíly , a . Řekněme, že trojice , a má (v určitém pořadí) rozdíly , a . Trojice , , a , , se shodují pouze v rozdílu mezi a , takže tento rozdíl musí být (je to jediný rozdíl, ve kterém se trojice , , a , , shodují).
Čísla a můžeme vzájemně zaměnit, takže si můžeme vybrat rozdíl mezi a takový, aby byl , a rozdíl mezi a . Ve trojici , a víme, že obě čísla a jsou buď největší nebo nejmenší. Vybereme je tak, že je to největší. Nyní máme dvě možnosti, jaký může být rozdíl mezi a čísly a .
Případ 1: Rozdíl mezi a je . Dostáváme, že ve trojici , a je jedno z čísel a největši a druhé nejmenší. Ve trojici , a jsme si ale vybrali, že je největší, takže je větší, než . Tím pádem víme, že ve trojici , , , je největší. Z toho plyne, že je o větší než a o větší než . Takže rozdíl mezi a je . Tohle je naše první řešení.
Případ 2: Rozdíl mezi a je . To znamená, že ve trojici , a je jedno z čísel a největší a druhé nejmenší. Obdobně jako v předchozí části víme, že je větší než , takže musí být nejmenší. Takže je o menší než a je o větší než . To znamená, že rozdíl mezi a je , což je naše druhé řešení.
Zjistili jsme, že naše neznámé hodnoty mohou být nebo . V našem původním problému to vyjadřuje fakt, že hodnoty napětí mohou být pouze nebo . Součet obou možných napětí je tedy .

.png)
.png)



.png)
.png)

.png)
.png)
.png)
.png)
.png)
.png)

.png)