Zadání a řešení úloh

Výsledek:

$2,45$

Matěj platil bankovkou v hodnotě $5e$ za tři zmrzliny, jejichž celková cena byla $0,80e+0,70e+1,05e=2,55e$. Prodavač mu tedy vrátil $5e-2,55e=2,45e$.

Výsledek:

$30$

Všechny strany čtverce mají stejnou délku, $0,5$ $m$. Všechny strany trojúhelníka mají rovněž stejnou délku. Jak je vidět, jedna z čar je jak stranou daného čtverce, tak i trojúhelníku. Všechny čáry na obrázku tedy musejí mít stejnou délku $0,5$ $m$. Obrázek se skládá z šesti takových čar a součet všech jejich délek je $6\cdot 0,5m=3m$. Každou sekundu Naty nakreslí $1$ $\mathrm{dm}$ čáry, takže za každých $10$ sekund nakreslí čáru o celkové délce $10\cdot 1\mathrm{dm}=10\mathrm{dm}=1m$. Aby měla celý obrázek, musí nakreslit třikrát delší čáru, takže jí kreslení zabere $3\cdot 10s=30s$.

Výsledek:

$1050$

I když dřevo plave (protože ho nadnáší vztlaková síla) nebude to mít žádný vliv na naměřenou hmotnost. Váha měří pouze celkovou hmotnost nádoby a jejího obsahu a ta není nijak ovlivněna silami mezi objekty v nádobě (vzhledem k tomu, že tyto objekty jsou v klidu). Díky tomu můžeme hmotnosti předmětů jednoduše sečíst: nádoba váží $250$ $g$, polovina litru vody $500$ $g$ (neboť hustota vody je $1\mathrm{kg}∕L$) a kus dřeva $300$ $g$. Váha tedy bude ukazovat hmotnost $250g+500g+300g=1050g$.

Výsledek:

$10$

Pojďme si vypsat všechny možnosti. Ty, kde je hodina matematiky na prvním místě, jsou MMFFF, MFMFF, MFFMF a MFFFM (M značí hodinu matematiky a F hodinu fyziky). Nyní si vypíšeme případy, kdy bude fyzika na prvním místě. Tyto možnosti jsou FMMFF, FMFMF, FMFFM, FFMMF, FFMFM a FFFMM. Jelikož libovolná kombinace hodin musí začínat matematikou nebo fyzikou, skutečně jsme zde vypsali všechny možnosti, jak si může Patrik rozvrh sestavit. Může si tedy vybrat mezi $10$ možnostmi.

Výsledek:

$10$

Do jednoho yardu se vejdou $3$ stopy a $12$ palců se rovná $1$ stopě. $1$ yard se tak rovná $3\cdot 12=36$ palcům. Šnek musí překonat vzdálenost $100$ yardů, tj. $100\cdot 36=3600$ palců. Jeden palec hřiště mu trvá přelézt $10$ sekund, takže přelezení celého hřiště mu bude trvat $10\cdot 3600=36000$ sekund. Každá hodina trvá $60$ minut a každá minuta má $60$ sekund, takže $1$ hodina = $60\cdot 60=3600$ sekund. Vidíme, že šnek potřebuje $36000÷3600=10$ hodin k přelezení celého hřiště.

Výsledek:

$81$

Zkusme nejdříve násobit menší čísla. $11\cdot 11=121$ a $111\cdot 111=12321$. Tvar výsledků není náhodný a lze proto odhadnout, že vynásobením čísla $111111111$ samo sebou získáme číslo $12345678987654321$, jehož ciferný součet je $1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1=81$.

Výsledek:

$46$

Nejprve spočítáme všechny čtverečky, které jsou vybarvené celé. Je jich $40$, takže na jejich vybarvení bude potřeba $40$ gramů inkoustu. Nyní se můžeme zabývat pouze čtverečky, které nejsou zcela vybarvené. Jak je vidět na obrázku, tvoří $6$ vybarvených trojúhelníků.

Všechny trojúhelníky ležící na stejné svislé čáře můžeme spárovat a vytvořit tak $3$ různé obdélníky. První obdélník pokrývá $3$ čtverečky; ten druhý $2$ a třetí $1$ čtvereček. Na jejich vybarvení potřebujeme $3+2+1=6$ gramů inkoustu. Takže aby Zuzka vybarvila celý obrázek, potřebuje $46g$ inkoustu.

Výsledek:

$8$

Pokud by Adam udržel tempo, uběhl by $20$krát vzdálenost $400m$ neboli $20\cdot 400m=8000m$ za jednu hodinu. To odpovídá rychlosti $8$ $\mathrm{km}∕h$. A co jeho průměrná rychlost? Jelikož Adam během prvních $20$ minut běží stejnou rychlostí, $8$ $\mathrm{km}∕h$ musí být zároveň Adamova průměrná rychlost během této části běhu.

Výsledek:

$5$

Jednosměrná cesta mezi konečnými stanicemi trvá

I se zpáteční cestou potrvá trasa jakémukoli autobusu $2\cdot 24\min =48\min$. Pokud nechceme, aby cestující čekali přes $10$ $\min$, musí v době, kdy přijíždí první autobus, na cestě být alespoň čtyři další autobusy. Potřebujeme tedy minimálně pět autobusů.

Výsledek:

$101$

Jarda potřebuje tisknout tolik stránek, aby je tiskárna v zasedací místnosti vytiskla alespoň o minutu rychleji než tiskárna v kanceláři (minutu totiž Jarda "vyplýtvá" na cestu ze zasedací místnosti zpět do kanceláře; cestu do místnosti totiž může absolvovat ještě během tisku).

Ze zadání vyplývá, že tiskárna v kanceláři vytiskne jednu stránku za $60s÷20=3s$, zatím co tiskárna v zasedací místnosti to zvládne za $60s÷25=2,4s$. Při časové úspoře $0,6s$ na jednu stránku je potřeba vytisknout více než $100$ stránek, aby výsledná časová úspora byla větší než $100\cdot 0,6s=60s=1\min$. Nejmenší počet stránek, které se Jardovi skutečně vyplatí tisknout v zasedací místnosti, je tedy $101$.

Výsledek:

$995$

Při zaokrouhlování na desítky je maximální rozdíl mezi výsledkem a Pedrovým číslem $5$. Nejmenší kladné celé číslo, které je výsledkem zaokrouhlování na tisíce je $1000$. Takže Pedrovo oblíbené číslo musí být alespoň $1000-5=995$. Můžeme vidět, že číslo $995$ splňuje všechny podmínky.

Výsledek:

$50$

Nina uběhla dva okruhy, takže celková dráha, kterou uběhla, byla $2\cdot 6\mathrm{km}=12\mathrm{km}$, s průměrnou rychlostí $8$ $\mathrm{km}∕h$. Proto byl celkový čas jejího běhu

Pokud Nina uběhla první okruh za $40$ minut, ten druhý musela zvládnout za $90-40=50$ minut.

Výsledek:

$12$

To, že někdo prohrál, se stalo přesně $10+9+8=27$krát. Z toho ale vyplývá, že $27$ je také celkový počet odehraných her. To znamená, že Ctibor musel vyhrát $27-7-8=12$ her.

Výsledek:

1

Pro libovolnou páku v rovnováze platí, že momenty tíhových sil, tj. součiny tíhových sil závaží vynásobené délkami příslušných ramen, jsou stejné. Aby byla tato podmínka splněna pro Patrikovy páky, musí pro každou z nich platit, že hmotnost závaží pověšeného na kratším konci musí být dvakrát větší než na druhém, delším konci.

Protože na kratším konci první páky je pověšená hmotnost $18$ $\mathrm{kg}$, součet hmotností závaží na druhé a třetí páce musí být $18\mathrm{kg}÷2=9\mathrm{kg}$. I pro druhou páku musí platit, že závaží na kratším konci je dvakrát těžší než součet hmotností na třetí páce. Z toho vyplývá, že závaží na kratším konci bude mít hmotnost $6$ $\mathrm{kg}$ a dvě závaží na třetí páce budou mít dohromady hmotnost $3$ $\mathrm{kg}$. Nakonec rozdělíme tuto hmotnost mezi zbývající dvě závaží ve stejném poměru $2:1$ a dospějeme k závěru, že závaží na delším konci třetí páky váží $1$ $\mathrm{kg}$.

Výsledek:

$40$

Pokud by voda nebyla odvedena záchytným systémem a ani by nepřetekla přes okraje střechy, na konci deště bychom na střeše našli kvádr tvořený vodou. Za předpokladu, že kapky deště padaly do bazénu rovnoměrně a stejně hustě jako na střechu, zvýšení hladiny vody v bazénu by přesně odpovídalo tloušťce onoho pomyslného kvádru tvořeného vodou. Tento kvádr má nám známý objem $4000L=4000{\mathrm{dm}}^3=4m^3$. Plocha jeho podstavy je stejná jako plocha střechy: $100$ $m^2$. Víme, že objem kvádru je součin jeho výšky a plochy jeho podstavy. Proto je jeho výška

Z toho vyplývá, že hladina v bazénu stoupla o $40$ $\mathrm{mm}$.

Výsledek:

$22$

V zadání je podmínka, že spolu mohou sousedit pouze buňky, jejichž rozdíl bude minimálně $2$. To znamená, že buňky lišící se pouze o $1$ spolu nemohou sousedit.

Pojďme se podívat na druhou a třetí buňku v prostředním řádku. Obě sousedí se všemi ostatními buňkami kromě jedné. Jaká čísla můžeme dát na tyto pozice? Pouze čísla, která se liší o $1$ od přesně jednoho dalšího čísla v rozmezí $1$ až $8$. Tuto podmínku zjevně splňují pouze čísla $1$ a $8$. Vzhledem k symetrii destičky nezáleží na tom, v jakém pořadí tam tato dvě čísla umístíme, a tak to uděláme tímto způsobem:

Obě čísla $1$ a $8$ mají pouze jedno číslo, se kterým mají rozdíl $1$. To jsou $2$ a $7$. Takže tato dvě čísla musíme umístit na dvě krajní pozice v prostředním řádku.

Buňka s číslem $2$ nemůže sousedit s číslem $3$, které tedy musí být pod, nebo nad číslem $1$. Ze stejného důvodu bude číslo $6$ umístěno pod, nebo nad buňku s číslem $8$. Tady máme dvě možnosti. Pokud umístíme $3$ a $6$ do stejného řádku, do zbývajícího řádku budeme muset umístit $4$ a $5$ vedle sebe, což nesmíme. Vydáme se tedy druhou možností, kdy umístíme čísla $3$ a $6$ do dvou různých řádků. Všimněme si, že $4$ a $3$ nemohou být v sousedních buňkách, takže nám zbývá přesně jedna možnost, jak tabulku sestavit:

Nakonec vypočítáme, že součet čísel sousedících s buňkou s číslem $4$ je $7+1+8+6=22$.

Výsledek:

$250$

Pro pohodlí si převedeme rychlost z kilometrů za hodinu na metry za sekundu: $108\mathrm{km}∕h=30m∕s$. Vlak jedoucí rychlostí $30$ $m∕s$ za dobu $75$ $s$ překoná vzdálenost $75s\cdot 30m∕s=2250m$. Lokomotiva tedy od doby, co vjela do tunelu, urazila $2250$ $m$. Protože tunel je dlouhý $2000$ $m$, po $75$ sekundách byla lokomotiva $2250m-2000m=250m$ za koncem tunelu. Vlak tedy musí být dlouhý $250$ $m$.

Výsledek:

57

Jelikož je průměrná délka Eliných tužek $12$ $\mathrm{mm}$, součet všech jejich délek musí být $6\cdot 12\mathrm{mm}=72\mathrm{mm}$. Aby byla jedna z tužek nejdelší, musí být ostatních pět co možná nejkratších. Proto musí mít délky $1$ $\mathrm{mm}$, $2$ $\mathrm{mm}$, $3$ $\mathrm{mm}$, $4$ $\mathrm{mm}$ a $5$ $\mathrm{mm}$, což je dohromady $15$ $\mathrm{mm}$ (tužku délky nula neuvažujeme). Na nejdelší tužku zbývá $72\mathrm{mm}-15\mathrm{mm}=57\mathrm{mm}$.

Výsledek:

4

Kámen ztrácí kinetickou energii v souladu se zákonem zachování energie kvůli působení síly tření, která koná práci. Na začátku má kámen s hmotností $m=18,6\mathrm{kg}$ a rychlostí $v=2m∕s$ kinetickou energii

Síla tření $F_t$, která kámen zpomaluje, se rovná součinu tíhové síly $F_G=\mathit{mg}$ a koeficientu tření $f=0,05$. Práce síly tření je pak

kde $s$ je vzdálenost, jež kámen na ledě urazí. Když se kámen na ledě zastaví, jeho kinetická energie se celkem promění na práci $W$. Z rovnosti pak můžeme následně spočítat vzdálenost $s$:

Kámen se tedy doklouže od Honzy do vzdálenosti $4m$.

Výsledek:

$50$

Protože body $A$ a $D$ jsou na ose úsečky $\mathit{BC}$, trojúhelníky $\mathit{ABC}$ a $\mathit{DBC}$ jsou rovnoramenné se základnou $\mathit{BC}$. S touto informací můžeme dopočítat velikosti úhlů u základny v trojúhelníku $\mathit{ABC}$ jako

a v trojúhelníku $\mathit{DBC}$ jako

Velikost úhlu $\mathit{ACD}$ je tedy $|\measuredangle \mathit{ACD}|=|\measuredangle \mathit{ACB}|-|\measuredangle \mathit{DCB}|=70\circ -20\circ =50\circ$.

Výsledek:

$2$

Spalné teplo dřeva je $21\mathrm{MJ}∕\mathrm{kg}=21000\mathrm{kJ}∕\mathrm{kg}$. Protože je účinnost jeho spalování pouze $0,5$ $\%$, spálením jenoho kilogramu dřeva získáme $21000\mathrm{kJ}∕\mathrm{kg}\cdot 0,005\cdot 1\mathrm{kg}=105\mathrm{kJ}$ energie, která se využije na ohřev vody. Aby se voda začala vařit, musíme ji z teploty $0{}^{\circ }C$ zahřát o $100{}^{\circ }C$. Na to je potřeba energie $0,5\mathrm{kg}\cdot 4,2\mathrm{kJ}∕(\mathrm{kg}{}^{\circ }C)\cdot 100{}^{\circ }C=210\mathrm{kJ}$, což je přesně dvojnásobek $105\mathrm{kJ}$. Káťa tedy na ohřev vody potřebovala $2\mathrm{kg}$ dřeva.

Výsledek:

$68$

Označme si $J$ jako počet jablečných bonbónů a $B$ jako počet banánových bonbónů. Na začátku bylo jablečných dvakrát více, což lze zapsat jako $J=2B$. Potom, co Lenka snědla $17$ jablečných a $17$ banánových bonbónů, zůstalo jí třikrát více jablečných bonbónů než banánových. To opět zapíšeme v jazyce rovnic jako $J-17=3(B-17)$. Dosazením $2B$ za $J$ (známe z první rovnice) dostaneme:

Na začátku tedy v sáčku bylo $B=34$ banánových bonbónů a $J=2B=68$ jablečných bonbónů.

Výsledek:

$20$

Nejdříve se podívejme na Jerryho první větu. Kdyby byla pravdivá, byla by sama o sobě Jerryho jedinou pravdivou větou, takže jeho druhá věta by musela být nepravdivá. Kdyby jeho první věta byla nepravdivá, druhá věta by také nemohla být pravdivá – v opačném případě by první věta musela být také pravdivá. Můžeme tak s jistotou tvrdit, že Jerryho druhá věta je lživá. Nemůžeme však zatím nic říct o jeho první větě.

Jerryho druhá věta je lživá. Potom musí Marcel říkat jednu pravdivou a jednu lživou větu. Zamysleme se, co by se stalo, kdyby jeho první nebo druhá věta byly pravdivé.

Kdyby byla pravda, že každý podezřelý řekl alespoň jednu nepravdivou větu, potom by Marcelova věta, že nemá Náboj, byla lživá, a musel by tedy být oným zlodějem. Potom by ale obě Matějovy věty musely být pravdivé, což by bylo nemožné, protože považujeme Marcelovu větu každý podezřelý řekl alespoň jednu nepravdivou větu za pravdivou.

Proto tou pravdivou větou musí být Marcelova druhá věta, tedy ta, že on nemá Náboj. Jelikož je jeho první věta lživá, musí zde být někdo, kdo řekl dvě pravdivé věty. To může být jenom Majo nebo Matěj. Jelikož ale Marcel nemá Náboj, Matěj nemohl říct dvě pravdivé věty. Proto ten, jehož obě věty jsou pravdivé, musí být Majo, který říká, že Matěj má Náboj. Matěj je tak zloděj.

Nakonec musíme spočítat, kolik vět bylo pravdivých. Dokázali jsme, že obě Majovy věty byly pravdivé. Z Matějových vět byla pravdivá jedna. Stejně tak jen druhá z Marcelových vět byla pravdivá. Nyní vidíme, že Jerryho první věta může být pravdivá i nepravdivá. Může to tak být $4$ nebo $5$ pravdivých vět. Součin možných počtů pravdivých vět tak je $4\cdot 5=20$.

Výsledek:

$216$

Knihy na zemi tvoří dohromady kvádr s výškou $8\cdot 5\mathrm{cm}=40\mathrm{cm}$, tudíž jejich těžiště leží ve výšce $20\mathrm{cm}=0,2m$ nad zemí. Pokud by knihy byly položené na poličce, vytvořily by kvádr s výškou $20$ $\mathrm{cm}$ a těžištěm ve výšce $10\mathrm{cm}=0,1m$ nad poličkou. Vzhledem k tomu, že je polička $1,6$ $m$ nad zemí, společné těžiště knih před a po vyskládání na poličku musí překonat výškový rozdíl $1,6m-0,2m+0,1m=1,5m$. Objem knih je $8\cdot 5\mathrm{cm}\cdot 15\mathrm{cm}\cdot 20\mathrm{cm}=12000{\mathrm{cm}}^3=12{\mathrm{dm}}^3$ a jejich hustota je $1200\mathrm{kg}∕m^3=1,2\mathrm{kg}∕{\mathrm{dm}}^3$. Jejich hmotnost je tedy $12{\mathrm{dm}}^3\cdot 1,2\mathrm{kg}∕{\mathrm{dm}}^3=14,4\mathrm{kg}$. Práce, kterou Marie musí vykonat, je rovna změně potencální energie knih v krabici na zemi a na poličce, jež činí $14,4\mathrm{kg}\cdot 10m∕s^2\cdot 1,5m=216J$.

Výsledek:

$51$

Klíčem k řešení úlohy je vzpomenout si, že pro každý trojúhelník platí trojúhelníková nerovnost. Ta nám říká, že součet délek libovolných dvou stran trojúhelníku musí být ostře větší než délka zbylé strany. Pojďme prozkoumat dvě kratší strany Jirkova trojúhelníku: $\mathit{BC}$ a $\mathit{AC}$. Víme, že jejich délky mohou být nanejvýš $8$ $\mathrm{cm}$ a $18$ $\mathrm{cm}$. Na základě toho můžeme říct, že aby mohl trojúhelník vůbec existovat, musí jeho třetí strana být kratší než $8\mathrm{cm}+18\mathrm{cm}=26\mathrm{cm}$, tedy může mít nanejvýš $25$ $\mathrm{cm}$. Trojúhelník s délkami stran $8$ $\mathrm{cm}$, $18$ $\mathrm{cm}$ a $25$ $\mathrm{cm}$ tedy může existovat a navíc jeho dvě kratší strany přispívají k obvodu trojúhelníku maximální povolenou délkou. Proto je nejvyšší možný obvod Jirkova trojúhelníku $8\mathrm{cm}+18\mathrm{cm}+25\mathrm{cm}=51\mathrm{cm}$.

Výsledek:

$5600$

Během zrychlování na dálnici vzrostla rychlost Sabinina auta trojnásobně. Protože kinetická energie roste s druhou mocninou rychlosti, při rychlosti $120$ $\mathrm{km}∕h$ je kinetická energie Sabinina auta $3^2=9$krát větší než energie při rychlosti $40$ $\mathrm{km}∕h$. Na zrychlení z $40$ $\mathrm{km}∕h$ na $120$ $\mathrm{km}∕h$ tedy Sabinino auto spotřebuje $9-1=8$krát více energie než na rozjezd na $40$ $\mathrm{km}∕h$, což činí $8\cdot 700\mathrm{kJ}=5600\mathrm{kJ}$.

Výsledek:

$1$

Pojďme prozkoumat všechny možné dvojice čísel z prvního papíru. Začněme dvojicemi, které obsahují číslo $1$. Rozdíly v těchto dvojicích jsou všechna čísla od $1$ to $99$. Dále se podívejme popořadě na dvojice, které obsahují číslo $2$ a zároveň neobsahují číslo $1$ (nebo alternativně na dvojice, v nichž je $2$ nejmenší číslo). Rozdíly čísel mezi těmito dvojicemi jsou čísla od $1$ do $98$. Analogicky můžeme pokračovat, dokud se nedostaneme ke všem dvojicím, kde je nejmenší číslo $99$. Taková dvojice existuje právě jedna (jsou to čísla $99$ a $100$). Ve všech případech, které jsme postupně prošli, bylo vždy mezi rozdíly přítomno pouze číslo $1$, a proto se číslo $1$ objevuje na druhém papíru nejčastěji.

Výsledek:

$10$

Označme si počet rezistorů $n$ a odpor každého z rezistorů jako $R$. Když připojíme multimetr k jednomu rezistoru, měříme odpor v obvodu se dvěma paralelně zapojenými větvami. V jedné větvi obvodu je jeden a ve druhé větvi je $n-1$ rezistorů. Pokud připojíme multimetr ke dvěma rezistorům, v jedné větvi budou $2$ rezistory a ve druhé bude $n-2$ rezistorů. To nás vede k následující soustavě rovnic vyplývající ze vztahu pro odpor paralelně zapojených rezistorů:

Po vynásobení rovnic jmenovateli dostaneme soustavu

Když roznásobíme závorky a rovnice upravíme, získáme:

Nyní odečteme druhou rovnici od první a dostaneme rovnici $R=n\mathrm{\Omega }$. Číselné hodnoty odporů jednotlivých rezistorů v ohmech jsou tedy stejné jako celkový počet zapojených rezistorů. Pokud tuto informaci dosadíme do rovnice $\mathit{nR}-R=9n\mathrm{\Omega }$, ziskáme

Tato rovnice je splněna pro $n=0$ nebo $n=10$. Výsledek $n=0$ ale nedává fyzikální smysl, a tak se musel Ninin náhrdelník skládat z $10$ rezistorů.

Výsledek:

$14$

Rozlišujme jednotlivé případy podle toho, s jakým vrcholem je úsečkou propojený vrchol $A$. Pokud je vrchol $A$ spojen s některým z vrcholů $C$, $E$ nebo $G$, potom odpovídající úsečka dělí zbývající vrcholy na dvě skupiny s lichým počtem vrcholů. Ty už ale nemohou být rozděleny do dvojic, tudíž nemůžeme nakreslit zbývající úsečky tak, aby byly splněny podmínky v zadání. Pokud je vrchol $A$ spojen s vrcholem $B$, bude nám zbývat spojit $6$ vrcholů. Máme $5$ možností jak toho docílit:

Kdybychom vrchol $A$ spojili s vrcholem $H$, získali bychom (na základě symetrie této situace) dalších $5$ způsobů. Pokud bychom jej spojili s vrcholem $D$, museli bychom nutně spojit vrcholy $B$ a $C$. Pro zbývající $4$ vrcholy máme následující dva způsoby:

Analogicky dostaneme $2$ další způsoby, pokud spojíme vrcholy $A$ a $H$. Postupně jsme tedy analyzovali všechny případy vrcholů, se kterými může být vrchol $A$ spojen. Proto můžeme s jistotou tvrdit, že existuje právě $5+5+2+2=14$ způsobů, jak může Laura úsečky nakreslit.

Výsledek:

$4000$

Pokud bychom položili nádobu o hmotnosti $m_{\text{nádoba}}=250g=0,25\mathrm{kg}$ na váhu a nalili do ní vodu s celkovým objemem $V=0,5L$, váha by ukázala hmotnost $m_1=m_{\text{nádoba}}+{\rho }_{\text{voda}}V=0,75\mathrm{kg}$. Po vložení oblázku na provázku váha ukázala hmotnost $m_2=1\mathrm{kg}$. Co způsobilo tento nárůst? Na oblázek působily dvě síly, gravitační a vztlaková. Vztlakovou silou na oblázek působila voda, a proto můžeme na základě zákona akce a reakce usoudit, že oblázek musel na vodu působit silou se stejnou velikostí, ale působící opačným směrem. Toto je zároveň jediná síla, která ovlivní hmotnost, kterou váha ve výsledku ukáže. Velikost síly odpovídající hmotnosti $m_2$, kterou váha ukázala, musí být tedy rovna součtu velikost tíhové síly od nádoby $F_G=m_{1}g$ a velikosti vztlakové síly působící na oblázek $F_{\mathrm{vz}}=V_{\text{oblázek}}{\rho }_{\mathrm{voda}}g$. Platí tedy

Objem oblázku pak můžeme vyjádřit jako

Z druhého vážení víme, že hmotnost oblázku je $m_{\text{oblázek}}=1\mathrm{kg}$. Proto jeho hustota musí být

Výsledek:

$6$

Protože je tření medzi rampou a medvídkem zanedbatelné, celková mechanická energie medvídka se během klouzání zachovává. Pokles potenciální energie Alexova medvídka musí proto v každém okamžiku odpovídat nárůstu jeho kinetické energie. Klesání rampy je rovno $\mathrm{\Delta }h=h(x)-h(0)=a{x}^2$. Proto musí platit:

kde $m$ je hmotnost Alexova medvídka a $v$ je jeho rychlost. Hmotnost $m$ ale nepotřebujeme znát, protože se nachází na obou stranách rovnice a můžeme ji z rovnice vykrátit. Platí tedy

Když do rovnice dosadíme hodnoty ze zadání, medvídek získá rychlost:

Výsledek:

$18$

Tři stěny původní kostky musely být namalovány oranžově a tři modře, jinak bychom našli alespoň jednu dvojici stěn namalovaných stejnou barvou. Navíc, aby měly protilehlé stěny různé barvy, musely mít tři stěny obarvené stejnou barvou jeden společný vrchol. Rozřezáním krychle na $125=5^3$ kousků získáme krychličky, jež mají $5$krát kratší hranu jako původní krychle.

Aby měla malá krychlička jednu stěnu modrou a jednu oranžovou, musí mít nutně jednu hranu společnou s původní kostkou, a to konkrétně hranu, která byla společná pro jednu oranžovou a jednu modrou stěnu původní kostky. Protože malé krychličky jsou $5$krát menší, podél každé takové hrany vzniklo $5$ krychliček. Ale z těchto pěti mají $2$ krychličky s původní krychlí společný i vrchol, a proto musí mít nutně obarvenou i třetí stěnu. Podél každé hrany původní kostky, kde se potkává oranžová a modrá stěna, bude tedy jen $5-2=3$ malých krychliček, které mají právě jednu modrou a jednu oranžovou stěnu. Jelikož původní kostka má $6$ hran kde se potkává oranžová a modrá stěna, existuje celkem $6\cdot 3=18$ malých krychliček vyhovujících podmínkám v zadání.

Výsledek:

$1413$

Číslo jež vznikne tak, že vynásobíme $b$-krát číslo $a$, označujeme jako $a^b=\underset{b\text{-krát}}{\underbrace{a\cdot a\cdot \dots \cdot a}}$. Vynásobíme-li $2021$ dvojek ($2^{2021}$) s výsledkem násobení $2021$ pětek ($5^{2021}$), dostaneme tím stejné číslo jako když vynásobíme $2021$ desítek ($10^{2021}$). Poslední jmenované číslo má velmi jednoduchý tvar – začíná se cifrou $1$ a pokračuje $2021$ nulami, tj. $1\underset{2021\text{-krát}}{\underbrace{00\dots 0}}$.

Ze zadání víme, že číslo $2^{2021}$ má $609$ cifer. Proto je určitě větší než číslo $1\underset{608\text{-krát}}{\underbrace{00\dots 0}}$ (tyto čísla jsou různá, neboť číslo $2^{2021}$ není násobkem pěti, a proto se nemůže končit cifrou $0$). Zároveň je ale toto číslo menší jako číslo $1\underset{609\text{-krát}}{\underbrace{00\dots 0}}$. Máme tak:

Označíme-li $n$ hledaný počet cifer čísla $5^{2021}$, stejně jako výše můžeme říci, že toto číslo je větší jako $1\underset{(n-1)\text{-krát}}{\underbrace{00\dots 0}}$ (znovu tyto čísla jsou různá, protože číslo $5^{2021}$ není násobkem dvou, a tudíž nemůže končit cifrou $0$). Zároveň je toto číslo menší jako $1\underset{n\text{-krát}}{\underbrace{00\dots 0}}$, takže platí:

Teď se podívejme na součin $2^{2021}\cdot 5^{2021}$. Nahradíme-li oba činitele menšími odhady, dostaneme i menší odhad tohoto součinu. Proto platí:

Podobně lze použít i větší odhady jednotlivých činitelů:

Jelikož při násobení mocnin desítky se ve výsledku pouze sčítává počet nul jednotlivých činitelů, dostáváme nerovnost:

Tím jsme součin $2^{2021}\cdot 5^{2021}$ ohraničili dvěma čísly. Jediné další číslo v tomto intervalu jež začíná jedničkou následovanou nuly je číslo obsahující $n+608$ nul. My ale již víme, že $2^{2021}\cdot 5^{2021}$ má přesně tento tvar. Jinými slovy, platí $2^{2021}\cdot 5^{2021}=1\underset{2021\text{-krát}}{\underbrace{00\dots 0}}$, tedy platí $n+608=2021$. Dostáváme tedy, že počet cifer čísla $5^{2021}$ je $n=2021-608=1413$.

Výsledek:

$60$

Pokud se písty nehýbají, musí na ně působit z obou stran stejně velké síly. Jelikož má píst mezi vodou a olejem stejnou velikost povrchu na obou stranách, musí být stejný i tlak, který na obě strany pístu působí. Tlak působící ve směru od pístu s vodou má dvě součásti – hydrostatický tlak a tlak vyvolaný vnější silou (váha předmětu na prvním pístu). Hydrostatický tlak vodního sloupce o výšce $h_1=20\mathrm{cm}$ je $p_{h1}=h_1{\rho }_{\mathrm{voda}}g$ a tlak vyvolaný závažím o hmotnosti $m_1=100g$ položeným na píst o povrchu $S_1=10{\mathrm{cm}}^2$ je $p_{t1}=m_{1}g∕S_1$.

Stejně tak hydrostatický tlak sloupce oleje o výšce $h_2=30\mathrm{cm}$ je $p_{h2}=h_2{\rho }_{\mathrm{olej}}g$, kde ${\rho }_{\mathrm{olej}}$ je hustota oleje, a tlak vyvolaný objektem s neznámou hmotností $m_2$ položeným na píst o povrchu $S_2=20{\mathrm{cm}}^2$ je $p_{t2}=m_{2}g∕S_2$. Rovnost celkových tlaků pak můžeme zapsat jako $p_{h1}+p_{t1}=p_{h2}+p_{t2}$, což lze rozepsat jako

Odsud můžeme vyjádřit $m_2$ jako

Matěj musí na druhý píst položit závaží o hmotnosti $60$ $g$.

Výsledek:

$15$

Nejdíve si vyberme dvě osoby, které si místa nevyměnily. Tyto dvě osoby dělí zbytek lidí na tři skupiny – nalevo od zafixovaných sedadel, mezi nimi a napravo od nich. V takovém rozdělení považujeme i skupinu o nula osobách za skupinu. Všimněme si, že člen každé skupiny musí sedět na sedačce, která původně patřila jinému členovi stejné skupiny (v opačném případě by se nejednalo o jejich souseda).

Nyní se podívejme na jeden okraj neprázdné skupiny – sedačku, která sousedí s fixovaným místem nebo která se nachází na okraji řady. Jelikož má tato sedačka ve skupině pouze jednoho souseda, osoba původně sedící na tomto místě měla jen jednu možnost, kam si přesednout. Stejně tak pro osobu sedící po výměně na sedačce na okraji existuje jen jedna možnost, jak mohla sedět předtím. To ale znamená, že zmíněný pár si vyměnil sedačky a vytvořil nový okraj. Tudíž ve skupině můžeme párovat osoby, které si jednoduše pouze vymění místa. To znamená, že každá skupina musí mít sudý počet členů tak, abychom byli schopni je vyměnit v souladu se zadáním.

Nyní tak můžeme každý takový pár "spojit" do jedné osoby, čímž vytvoříme $4$ "dvojosoby". Otázkou zůstává, kolika způsoby mezi ně můžeme rozmístit dvě fixované osoby? Se dvěma fixovanými osobami máme $6$ pozic, na které může být osoba umístěna. Můžeme tak první fixovanou osobu umístit $6$ způsoby a druhou $5$ způsoby, což nám dává $6\cdot 5=30$ způsobů. Nicméně zatím jsme každou možnost počítali dvakrát, protože pokud vyměníme dvě fixované osoby, nezískáme novou možnost. To znamená, že osoby se mohly vyměnit $15$ různými způsoby.

Výsledek:

$2$

Když Jonáš natáhne spojené pružinky silou $F$, obě se natahují touto silou. Pružinka s tuhostí $k_1=3N∕\mathrm{cm}$ se natáhne o $F∕k_1$. Obdobně pružinka s tuhostí $k_2=6N∕\mathrm{cm}$ se prodlouží o $F∕k_2$. Celkové prodloužení spojených pružinek je pak součtem těchto prodloužení. Když si označíme neznámou tuhost spojených pružinek jako $k$, lze toto prodloužení zapsat i jako $F∕k$. Musí proto platit

Spojené pružinky tak mají tuhost

Výsledek:

$100$

Po tom, co Jaro provede $n$ tahů, žeton se pohne o $2+4+6+\cdots +2n$ polí. Když vytkneme číslo $2$ a využijeme vzorec pro součet prvních $n$ kladných celých čísel, získáme

Abychom dostali žeton po posunutí o $n(n+1)$ polí na pole začáteční, číslo $n(n+1)$ musí být dělitelné $2020$. Prvočíselný rozklad čísla $2020$ je $2020=2\cdot 2\cdot 5\cdot 101$, číslo $n(n+1)$ tak musí být dělitelné prvočíslem $101$. Nejmenší $n$, proto které toto nastane, je $n=100$, tj. když $n+1=101$. V tomto případě navíc platí, že $n=100$ je násobek $2\cdot 2\cdot 5=20$ a tudíž platí, že pro $n=100$ je číslo $n(n+1)$ dělitelné $2020$.

Tím jsme dokázali, že po $100$ tazích žeton dorazí na počáteční pole a že by tato situace nenastala po méně tazích. Jaro tak musí udělat nejméně $100$ tahů.

Výsledek:

$10$

Jediné vnější síly působící na oba míče jsou tíhová síla a síla, kterou na míče působí podložka. Obě tyto síly působí ve svislém směru, což znamená, že těžiště našeho systému se vodorovném směru nikam nepohne. Větší míč se proto posune o takou vzdálenost, o jakou je v původní poloze vzdáleno společné těžiště od středu většího míče.

Těžiště většího míče je v jeho středu (vzdáleno je tedy o $0$ $\mathrm{cm}$ v horizontálním směru). Těžiště menšího míče je také v jeho středu, tj. ve vzdálenosti $20$ $\mathrm{cm}$ od středu většího míče. Jelikož oba míče mají stejnou hmotnost, těžiště celého systému je ve středu úsečky spojující těžiště míčů, tj. ve vzdálenosti $10$ $\mathrm{cm}$ od středu většího míče. Větší míč se tedy pohne rovněž o $10$ $\mathrm{cm}$.

Výsledek:

$22$

Bořek tahá za lano silou $F=800N$. Napětí v laně je tak stejné jako síla $F$ v každém jeho bodě. To platí také pro spodní kladku a obě strany lana, které je kolem ní. Lano proto na spodní kladku působí silou $2F$, která kladku tahá vytahuje nahoru. To platí pro každou smyčku kolem spodní kladky, tzn. pro $n$ je celková síla působící na spodní kladku $2\mathit{nF}$. Aby mohl Bořek zvednou Béďu o hmotnosti $m=3500\mathrm{kg}$, musí tato síla být větší než tíhová síla působící na Béďu. Proto

Můžeme vidět, že lano se musí kolem spodní kladky otočit alespoň $22$krát.

Výsledek:

$3$

Poloměr menší kružnice označíme jako $r$. Nakreslíme-li si náčrtek, můžeme si zapsat některé délky:

Zaměřme se na zvýrazněný pravoúhlý lichoběžník. Jeho základny jsou poloměry větší a menší kružnice. Rameno, které je kolmé k základnám, má také délku rovnou poloměru větší kružnice a zbývající rameno má délku, která je rovna součtu poloměrů větší a menší kružnice. Jak lze vidět i z obrázku, lichoběžník lze rozdělit na obdélník a pravoúhlý trojúhelník. V tomto trojúhelníku jsou délky odvěsen $12$ $\mathrm{cm}$ a $12\mathrm{cm}-r$, délka přepony je pak $12\mathrm{cm}+r$. Z Pythagorovy věty tedy platí

Poloměr menší kružnice je $r=3\mathrm{cm}$.

Výsledek:

$39$

Když Lucie zamrazuje oblázek a skleněnku do krychle, nemění její objem, ale zvyšuje hmotnost, což mění její průměrnou hustotu. Pokud se krychle nepotopí, objem ponořené části je přímo úměrný průměrné hustotě krychle, tedy i výška ponořené části musí být přímo úměrná průměrné hustotě. Navíc přidání oblázku (nebo skleněnky) vždy zvýší průměrnou hustotu o stejnou hodnotu. Proto jejich zamrazení do krychle zvýší výšku ponořené části krychle o stejnou hodnotu, což také znamená, že sníží výšku části nad hladinou o stejnou hodnotu.

Když jsme v krychli měli pouze oblázek a poté přidali skleněnku, výška neponořené části klesla o $3,2\mathrm{mm}-1,9\mathrm{mm}=1,3\mathrm{mm}$. Přidání skleněnky tak vždy sníží výšku nepotopené části o $1,3\mathrm{mm}$. Pokud si vezmeme krychli pouze se skleněnkou a tu odstraníme, krychle obsahující pouze led by měla výšku nepotopené části $2,6\mathrm{mm}+1,3\mathrm{mm}=3,9\mathrm{mm}$.

Čistě ledová krychle s délkou strany $a$ má objem $V=a^3$ a hmotnost $m={\rho }_{\mathrm{led}}V$. Je-li objem ponořené části $V^{\prime }=a^2(a-h)$, kde $h=3,9\mathrm{mm}$ je výška neponořené části, potom z Archimedova zákona získáváme

Luciina krychle tak má délku strany $39\mathrm{mm}$.

Výsledek:

$24$

Na první pohled to vypadá, že mezi čísly ve druhém seznamu neplatí žádná zákonitost. Opak je ale pravdou. Když si napíšeme některé z prvních cifer z druhého seznamu, můžeme se všimnout, že číslo $1$ se zde objevuje až podezřele často. Od něj čísla vzrůstají, dokud se nedostanou zpět k $1$. Pojďme se proto zaměřit na to, jaká čísla mohou ve druhém seznamu následovat po sobě:

• Číslo $1$ může být následováno jen $2$ nebo $3$.
• Číslo $2$ může být následováno jen $4$ nebo $5$.
• Číslo $3$ může být následováno jen $6$ nebo $7$.
• Číslo $4$ může být následováno jen $8$ nebo $9$.
• Čísla $5$, $6$, $7$, $8$ a $9$ mohou být následovány pouze číslem $1$, protože desítka se přesouvá na další cifru.

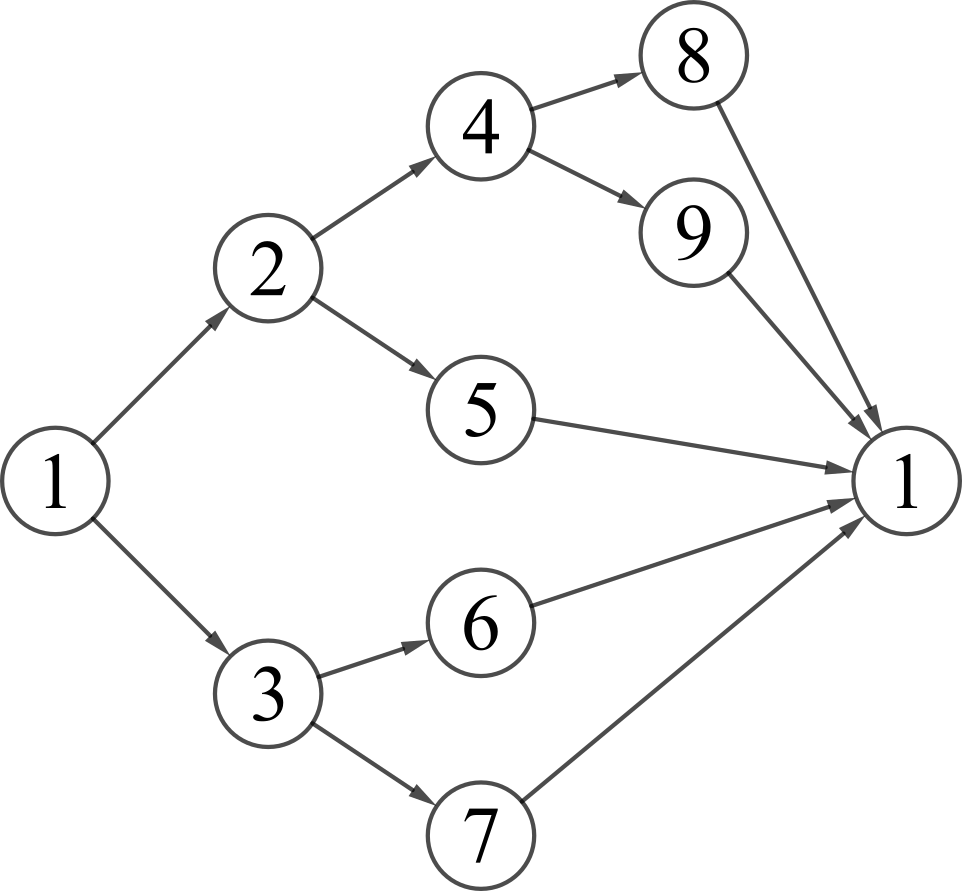
Možné posloupnosti čísel ve druhém seznamu jsou znázorněna na obrázku níže:

Můžeme tedy vidět, že jedničky rozdělují čísla ve druhém seznamu na oddělené bloky. Navíc, téměř všechny bloky se skládají ze třech čísel (počítáme zde i číslo $1$). Existují pouze dva bloky, které obsahují $4$ čísla – blok $1$, $2$, $4$, $8$ a blok $1$, $2$, $4$, $9$. Toto jsou navíc jediné bloky, které obsahují číslice $8$ a $9$. Nyní si musíme uvědomit ještě jednu věc. Když narazíme ve druhém seznamu na číslo $1$, potom odpovídající číslo v prvním seznamu bude mít o cifru více než předchozí číslo v tomtéž seznamu – to proto, že číslo $1$ se objevuje jako první cifra v okamžiku, kdy číslo v prvním seznamu "přeroste" před desítku.

Nyní poskládáme všechno dohromady. První blok z druhého seznamu odpovídá jednociferným číslům z prvního seznamu. Navíc, poslední tři čísla ve druhém seznamu jsou $1$, $2$, $5$, tudíž vytvářejí kompletní blok který odpovídá posledním, $167$ciferným číslům z prvního seznamu. Druhý seznam proto musí obsahovat $167$ bloků čísel. Pokud by všechny bloky obsahovaly $3$ čísla, měl by druhý seznam dohromady pouze $3\cdot 167=501$ čísel. Čtyři čísla tak musí být obsažena v $555-501=54$ blocích. Ve druhém seznamu se tak musí čísla $8$ nebo $9$ objevit $54$krát. Jelikož se číslo $8$ objevuje $30$krát, číslo $9$ se musí ve druhém seznamu objevit celkem $54-30=24$krát.