Problem statements

Rezultat:

2012. godine stablo jabuke bilo je visoko . Svake od idućih deset godina naraslo je dodatnih . Dakle, 2022. godine stablo jabuke visoko je .

Rezultat:

Dovoljno je izbrojiti koliko je stranica kvadrata Ana prehodala - , što znači da je prošla .

Rezultat:

Prosječna brzina omjer je ukupne udaljenosti koju je Juraj pretrčao i vremena koje mu je za to bilo potrebno. Iz grafa možemo pročitati da je Juraj pretrčao udaljenost od tijekom , što znači da mu je prosječna brzina bila .

Rezultat:

Danijel najprije mora skupiti slovo N. Uzme li N koje se nalazi dva polja desno od početne pozicije žetona, mora nastaviti prema slovu Á s donje desne strane slova N. Odatle ne može doći do slova B krećući se samo prema dolje ili udesno. Dakle, Danijel mora skupiti slovo N neposredno ispod početne pozicije žetona.

Nadalje, ako želi skupiti slovo Á tri polja desno od skupljenog N, dolazi do istog problema sa slovom B kao u prethodnom odlomku. Iz tog razloga Danijel skuplja slovo Á odmah ispod skupljenog N.

Nastavi li dalje prema slovu B u donjem lijevom kutu ploče, samo na jedan način može doći do slova J u donjem desnom kutu. Budući da će, krećući se na taj način, putem skupiti i slovo O, ovo je jedno od mogućih kretanja žetona.

S druge strane, nastavi li Danijel prema slovu B u trećem retku i trećem stupcu ploče, ponovno ima dvije mogućnosti za skupiti slovo O. Odabere li O u posljednjem redu, samo na jedan način može stići do slova J. Međutim, odabere li desno O, postoje tri načina na koja može doći do J.

Svi su mogući putevi ucrtani na ploči ispod:

Dakle, uz zadana pravila Danijel može pomicati žeton na načina.

Rezultat:

Spominjani smjerovi odnosit će se na skicu. Zraka se odbija od desnog zida i pogađa lijevi nakon dodatnog metra u visinu. Dakle, pogodit će lijevi zid metra iznad mjesta s kojeg je poslana. Nakon toga, zraka se odbija od lijevog zida i pogađa desni dodatnih metar iznad, tako da točno pogodi kut u kojem se nalazi balon. Putanja laserske zrake prikazana je na donjoj slici:

Zraka će se reflektirati puta.

Rezultat:

Laura na svom biciklu može prijeći kilometra u jednom satu. Budući da su kilometra doškole, Laura u jednom satu biciklom može prijeći doškola. Nadalje, jedan školskisat sastoji se od sata. Ako Laura može prijeći doškola u jednom satu, tada će u tri četvrtine sata (tj. u jednom školskisatu ) prijeći doškola. Dakle, Laura vozi bicikl brzinom doškola na školskisat.

Rezultat:

Podijelimo moguće brojeve po slučajevima ovisno o prvoj znamenki. Jedini broj koji počinje s nulom je , no on nije prirodan pa ga Alex ne smatra padajućim. Ako je prva znamenka , može ju slijediti ili broj može biti jednoznamenkast. To nam daje brojeve i . Ako broj počinje znamenkom , nakon nje mogu doći , ili ništa. Dakle, mogućnosti su , , , . Konačno, ukupno postoji padajućih brojeva.

Rezultat:

Matko je stazu od pretrčao brzinom . To znači da je cijelu utrku pretrčao za .

Mate je vozio bicikl brzinom , stoga mu je za cijelu duljinu staze trebalo . Budući da je Mate Matku u početku dao minuta prednosti, završio je utrku nakon što je Matko počeo.

Dakle, Mate je završio prije Matka.

Rezultat:

Mogu li brojevi sjedala sadržavati znamenke , , , , ili ? U tom bi slučaju broj sjedala ili obrnuti broj sjedala morao biti djeljiv s dva ili pet. Prema tome, željeni brojevi sjedala u zapisu ne mogu sadržavati navedene znamenke, već samo , , ili . Sljedećih brojeva zadovoljava taj uvjet:

Od navedenih, ovi brojevi nisu prosti: , , , , i , stoga ih odbacujemo. Također odbacujemo broj jer u obrnutom poretku dobivamo složen broj. Dakle, mogući brojevi sjedala su:

Zaključujemo da je Matej mogao nabaviti najviše ulaznica.

Rezultat:

Pomoću Pitagorinog poučka možemo izračunati udaljenost koju dijete prijeđe spuštajući se niz tobogan. Ona iznosi . S obzirom da je vrijeme potrebno za spuštanje , djetetova prosječna brzina je .

Rezultat:

Pravokutnik može biti podijeljen na dva manja pravokutnika samo dužinom paralelnom s dvjema stranicama velikog pravokutnika. Duljina te dužine jednaka je duljini stranica pravokutnika s kojima je paralelna.

U zadatku je rečeno da promatramo pravokutnik s opsegom i jednom stranicom duljine . Druga je stranica u tom slučaju duljine tako da vrijedi jednakost . Iz toga slijedi da je .

Prva rečenica ovog rješenja kaže da duljina stranice mora odgovarati duljini staze koja dijeli vrt na dva sukladna pravokutnika. Dakle, ako Kristina odluči napraviti stazu na drugi način, ona će biti duga .

Rezultat:

Primjenjujemo zakon akcije i reakcije koji kaže da, ukoliko objekt djeluje na objekt silom , tada objekt također djeluje na silom jednakog iznosa, ali suprotne orijentacije. Što se našeg zadatka tiče, Zemlja privlači Matea silom od , stoga i Mateo mora djelovati na Zemlju gravitacijskom silom jednakog iznosa. Dakle, sila iznosi .

Rezultat:

Označimo traženu udaljenost sa . Da Sabina nije stala da se odmori, vrijeme potrebno da prijeđe udaljenost iznosilo bi . Međutim, budući da je stala na minuta, traženu je udaljenost prošla za . Iz tog je razloga Sabinina prosječna brzina bila , što nas dovodi do sljedeće jednadžbe: Dakle, Sabina je ukupno prevalila udaljenost od .

Rezultat:

Predviđanje koje se od točnog broja razlikuje za mora biti najveće ili najmanje od svih. Kad bi bilo najmanje, točan broj riješenih zadataka morao bi biti ili ili . Prva opcija ne dolazi u obzir jer bi se druga predviđanja razlikovala od točnog broja za više od . U drugom slučaju razlike preostalih pokušaja i rješenja bile bi , i , što ne odgovara uvjetima zadatka.

Prema tome, član ekipe koji je predvidio točno riješenih zadataka morao se prevariti za . Kao u prošlom razmatranju, predviđanje ne može biti , već . U tom su slučaju preostale razlike , i , što se slaže s ostalim razlikama iz zadatka.

Dakle, ekipa je uspješno riješila zadataka.

Rezultat:

Razmislimo što znači kada netko kaže da osoba jest ili nije mafija. Primjerice, Ana kaže da je Danijel mafija. Ako govori istinu (odnosno ako nije mafija), Danijel je mafija. Ako laže (tj. ona je mafija), Danijel nije mafija. Dakle, Ana i Danijel su sa suprotnih strana – jedno od njih je mafija, a drugo nije. Nadalje, pogledajmo što kaže Bruno. Ako govori istinu (tj. nije mafija), Cvijeta također nije mafija. Međutim, ako Bruno laže (odnosno ako je mafija), Cvijeta je također mafija. Prema tome, Bruno i Cvijeta ili su oboje mafija ili nijedno nije mafija. Slično, Danijel i Erik su također na istoj strani.

Pretpostavimo da je Ana mafija. Tada bi uz nju morali biti mafija ili Bruno i Cvijeta, ili Danijel i Erik. U tom bi slučaju najmanje troje prijatelja bilo mafija, što ne odgovara pravilima igre. Dakle, Ana svakako nije mafija pa govori istinu - Danijel je mafija. Prije smo zaključili da je Danijel na istoj strani kao i Erik, koji prema tome također mora biti mafija. Preostalo dvoje, Bruno i Cvijeta, nisu mafija.

Zaključujemo da su mafija Danijel i Erik s ukupnim zbrojem .

Rezultat:

Označimo veličinu Mislavove datoteke s . Vrijeme za učitavanje bez kompresije iznosi . Ako ju odluči komprimirati, sama kompresija trajat će . Tada će veličina datoteke biti . Nakon sekundi Mislav kreće s učitavanjem datoteke na disk, što traje . Dakle, cijeli postupak s kompresijom traje . Zadatak navodi da je to jednako vremenu učitavanja bez kompresije, što dovodi do sljedeće jednadžbe, koju rješavamo ovako: Zaključujemo da je veličina Mislavove datoteke .

Rezultat:

Primijetimo da je opseg cijelog vrta jednak zbroju opsega cvjetnjaka s opsezima i te cvjetnjaka s opsegom označenim upitnikom. To je zato što neke stranice ta tri cvjetnjaka mogu biti pomaknute do ruba vrta i tako tvoriti opseg cijelog vrta:

Slijedi da je opseg cvjetnjaka označenog upitnikom jednak .

Rezultat:

Što je veća udaljenost na kojoj Adrijan koči, manju silu treba primijeniti. Pretpostavimo da automobil koči na udaljenosti . Da bi se zaustavio, automobil mora izvršiti rad kako bi savladao silu kočenja na račun svoje energije, u ovom slučaju svoje kinetičke energije.

Kinetička energija automobila mase i brzine je . Rad istog iznosa mora izvršiti sila iznosa , kojom automobil svladava silu kočenja istog iznosa. Ova sila obavlja na putu rad . Ovo dovodi do jednadžbe

Dakle, sila kočenja koja djeluje na automobil mora biti iznosa najmanje:

Rezultat:

Cijena od 23 se ne može nikako platiti. Možemo koristiti ili kovanicu od , inače bismo premašili cijenu od 23. U oba slučaja ne možemo platiti ostatak s kovanicama od . Međutim, možemo platiti bilo koju cijenu veću od . Započnimo s cijenama od (), () i ().. Ako možemo platiti ove tri cijene, možemo platiti i bilo koju višu cijenu – potreban nam je samo dovoljan broj kovanica u vrijednosti od . Dakle, najveća cijena koju Maša ne može platiti bez kusura je .

Rezultat:

Cijela je situacija osno simetrična, s obzirom na os definiranu spojnicom obaju kugli. Ta će simetrija biti očuvana i nakon sudara, kada kugle oforme veće tijelo. Kada bi se to tijelo pomicalo lijevo ili desno, sustav više ne bi bio simetričan. Stoga, veće tijelo nastalo spajanjem dvaju manjih ostat će mirovati.

Tijekom sudara, svaka od kugli izgubi svoji kinetičku energiju, koja se, po pretpostavci zadatka, pretvara u toplinu. Toplina prelazi na novonastalo tijelo te se ono zagrijava. Svaka od kugli (mase i brzine iznosa ) nosi kinetičku energiju . Zajedno, kugle nose kinetičku energiju iznosa . Ova energija prelazi na novonastalo tijelo u obliku topline. To tijelo ima masu (sadrži obje kugle, svaka mase ), specifični toplinski kapacitet , a temperatura će mu se promijeniti za . Iz toga slijedi: Ako je temperatura kugli prije sudara bila , tada će temperatura tijela nakon sudara biti:

Rezultat:

Kako bi klackalica bila u ravnoteži, zakretni moment na obje strane klackalice moraju biti isti. Dan, koja ima masu , sjedi na udaljenosti od od točke rotacije. Na nju djeluje gravitacijska sila i ona djeluje na klackalicu silom jednake veličine. Ta sila djeluje sa zakretnim momentom: Kocke sa druge strane moraju djelovati sa jednakim zakretnim momentom. Pretpostavimo da je stavljeno n kocki. U zadatku je rečeno da je svaka kocka ima masu i duljinu . N kocki zajedno ima masu i tvore pravokutnik duljine . Centar mase tog pravokutnika je u točki od točke rotacije klackalice, stoga je to udaljenost na kojoj gravitacijska sila pravokutnika (napravljenog od kocki) djeluje na klackalicu. Tada je zakretni moment kojim taj pravokutnik djeluje na klackalicu: Zakretni momenti i moraju biti jednaki. Izjednačavanjem gornje dvije jednadžbe dobivamo: Dakle, broj kocki koje je Nina morala staviti na klackalicu je:

Rezultat:

Razmislimo o znamenkama koje mogu biti na mjestu jedinice. Znamenke , i ne mogu biti na mjestu jedinice jer bi tada brojevi bili djeljivi s i ne bi bili prosti. Slično tako znamenka ne može biti na mjestu jedinice jer bi tada broj bio djeljiv s 5. Stoga znamo da će znamenke , , i biti na mjestima desetica a ostale znamenke (, , i ) će biti na mjestu jedinica. Znači, jedina, i stoga je najveća moguća suma ta 4 prosta broja jednaka .

Napomena: Od karata se stvarno mogu napraviti prosti brojevi, primjerice: , , and .

Rezultat:

Pravci u ravnini, koji se ne sijeku u nijednoj točki, moraju biti paralelni. Dakle, cilj je prebrojati broj parova paralelnih pravaca zadanih sa tih točaka. Označimo te točke sa , , , , , i . Prvo ćemo naći sve pravce zadane sa neke dvije točke koji su paralelni pravcu . To su pravci i , zato što je pravilni -erokut simetričan s obzirom na simetralu dužine . Zbog te simetrije, pravci , i su okomiti na simetralu pravca , i stoga su paralelni. Na taj način dobijemo para paralelnih pravaca. Ponavljajući istu ideju za pravce , , , , i , dobijemo para paralelnih pravaca u svakom od tih slučajeva. Svaki pravac zadan točkama od do je paralelan jednom od pravaca , , , , , ili (ovih pravaca se u parovima sjeku). Dakle, na taj način dobijemo sve parova paralelnih pravaca.

Sveukupno, Dora može nacrtati par pravaca na način.

Rezultat:

Potencijalna energija loptice kad je bačena iznosi , gdje je njezina masa, je visina s koje Serena baca lopticu i je gravitacijsko ubrzanje. Ako sa označimo brzinu, onda kinetička energija loptice kad je bačena iznosi . Tijekom cijelog gibanja, ukupna energija loptice ostaje ista. Stoga je suma konstantna u svakom trenutku, pa tako i neposredno prije dodira sa zemljom. U tom trenutku, visina loptice je nula pa joj i potencijalna energija iznosi nula. Zbog toga je ukupna energija loptice u tom trenutku jednaka kinetičkoj energiji. Ako sa označimo brzinu loptice neposredno prije nego dodirne zemlju, dobijemo jednadžbu: Brzina loptice u trenutku prije nego dodirne zemlju stoga iznosi:

Rezultat:

Jedini jednoznamenkasti broje koji je 13 puta veći od zbroja svojih znamenki je 0. Čak i da smatramo nulu prirodnim brojem (u nekim granama matematike 0 se smatra prirodnim brojem, u nekima ne), ona ne bi promijenila krajnji zbroj svih brojeva koje je Fran našao.

Ako postoji dvoznamenkasti broj koji zadovoljava uvjete zadatka, bio bi oblika , gdje su i njegove znamenke. Međutim, kada ovaj broj pomnožimo sa 13 dobijemo broj oblika , a . Zaključujemo da ne postoji dvoznamenkasti broj 13 puta veći od zbroja svojih znamenki

Nastavimo s troznamenkastim brojevima, od kojih se svaki može zapisati u obliku . Sigurno vrijedi . Kada upotrijebimo uvjet zadatka, dobijemo: Ako , imamo tri mogućnosti za znamenke and . Za vrijednosti dobijemo , i , što pridružujemo brojevima , i . Nemamo više mogućnosti za jer, pošto je , za bismo dobili , a znamo za desnu stranu jednadžbe da vrijedi 45. Drugim riječima, nema brojeva za koje bi vrijedilo . Time smo riješili slučaj za troznamenkaste brojeve.

Za četveroznamekaste brojeve najveći zbroj njihovih znamenaka iznosi , pa bi to pomnoženo sa 13 svakako bilo manje od (naravno, mogli smo izračunati i , ali čak i ovakvo grubo zaokruživanje može nas dovesti do sljedećeg zaključka). Stoga, možemo reći da kada zbroj znamenki četveroznamenkasnog broja pomnožimo sa 13, rezultat sigunro neće biti četveroznamekasti broj. Pa tako Fran nije mogao naći ni jedan takav broj, kao ni broj sa više znamenaka od 4.

Zbroj svih brojeva koje je Fran našao iznosi .

Rezultat:

Dijagonale kvadrata su jednake duljine te međusobno okomite. Znamo da je duljina dijagonale znaka . Svaka dijagonala dijeli kvadrat na dva sukladna trokuta čija je visina polovica druge dijagonale. Takav trokut ima površinu . Cijeli znak se sastoji od dva takva trokuta pa je površina znaka = 72 dm².

Žuti dio zauzima cijelog znaka pa je žuta površina . Stranica žutog kvadrata je tada dugačka .

Rezultat:

Označimo duljinu staze sa d. Iz slušaja kada Matija samo stoji na stazi možemo saznati brzinu staze. Matija treba da dođe s jednog kraja na drugi, pa je brzina staze . Slično, iz slučaja gdje Matija hoda pored staze možemo pronaći njenu brzinu. Treba joj , stoga joj je brzina .

Kad Matija hoda u smjeru suprotnom stazi, njena brzina je . Pa joj do kraja staze treba: U slučaju kada Matija hoda u smjeru kao u staza, brzina joj je . Do kraja staze treba joj: Iz ovoga zaključujemo da kada Matija hoda na stazi u smjeru suprotnom od gibanja staze, treba joj više vremena koje iznosi:

Rezultat:

Opišimo prvo kako izgledaju skupovi i . Funkcija (znana još i kao apsolutna vrijednost broja) "briše" predznak ispred broja .

Rastavimo slučajeve za skup , tj. jednadžbu . Ako je i , vrijedi . Uvjet je tada ekvivalentan , dakle , što je pravac koji prolazi točkama i . S obzirom da je ovo rješenje samo za slučaj i , zanima nas samo dužina koja spaja te dvije točke. Razmatranjem svih mogućnosti predznaka i dobivamo da sadrži dužine između parova točaka i , i , i te i . To jest, skup je kvadrat s vrhovima u točkama , , i .

Nastavimo sa skupom koji je opisan relacijom . Da bi vrijednost funkcije bila , barem jedan od brojeva i mora biti jednak , dok drugi mora biti manji od . Ako , tada je ili . U tom slučaju mora vrijediti i , to jest . Za , ovo zadovoljavaju točke na dužini s vrhovima u i , dok za to zadovoljavaju točke na dužini s vrhovima u i . Sličnim obrazloženjem rješavamo slučaj . Ovaj slučaj dodaje skupu dužinu s vrhovima u i i dužinu s vrhovima u i . To jest, skup je isto kvadrat, ali s vrhovima u točkama , , i .

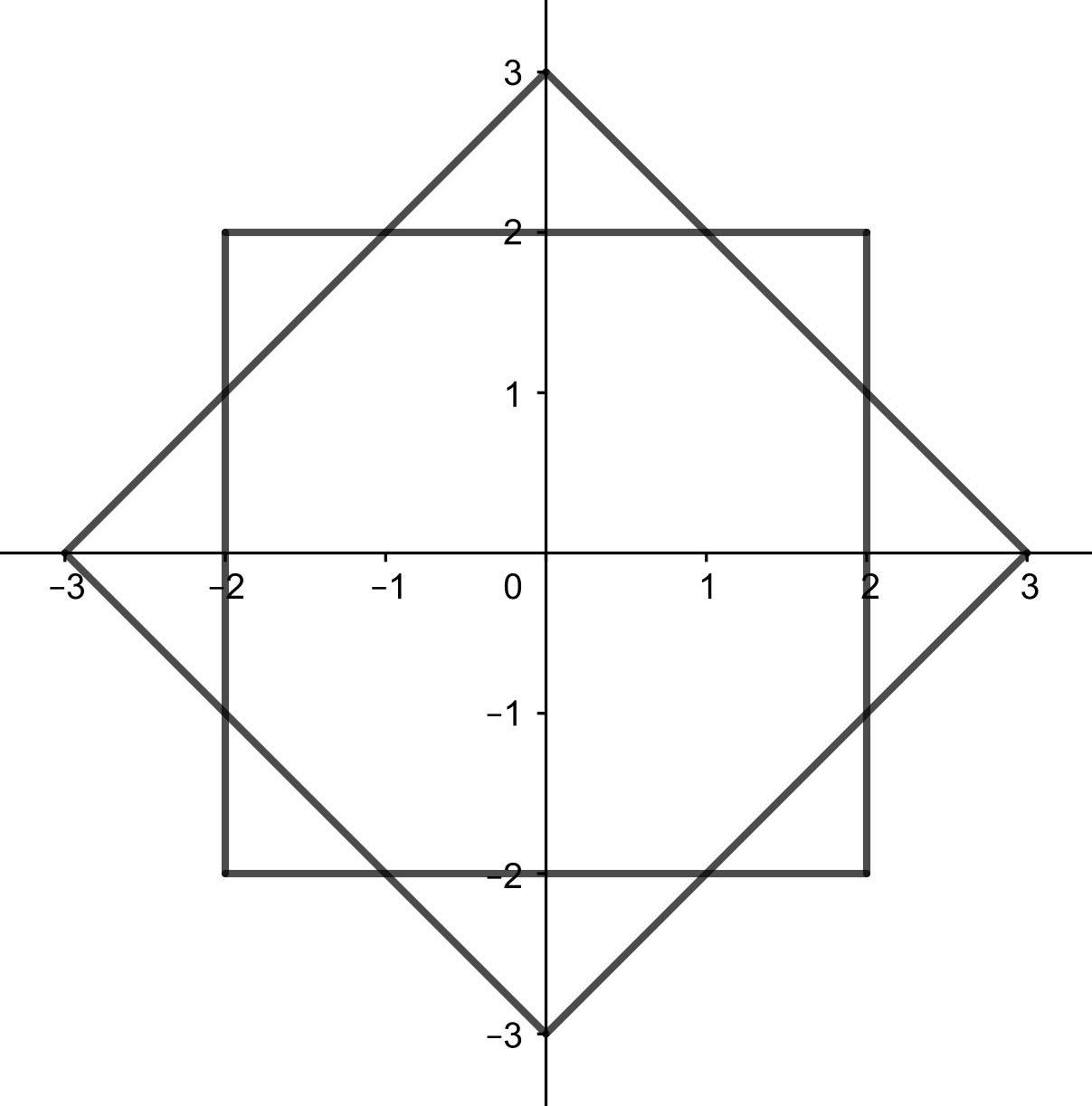
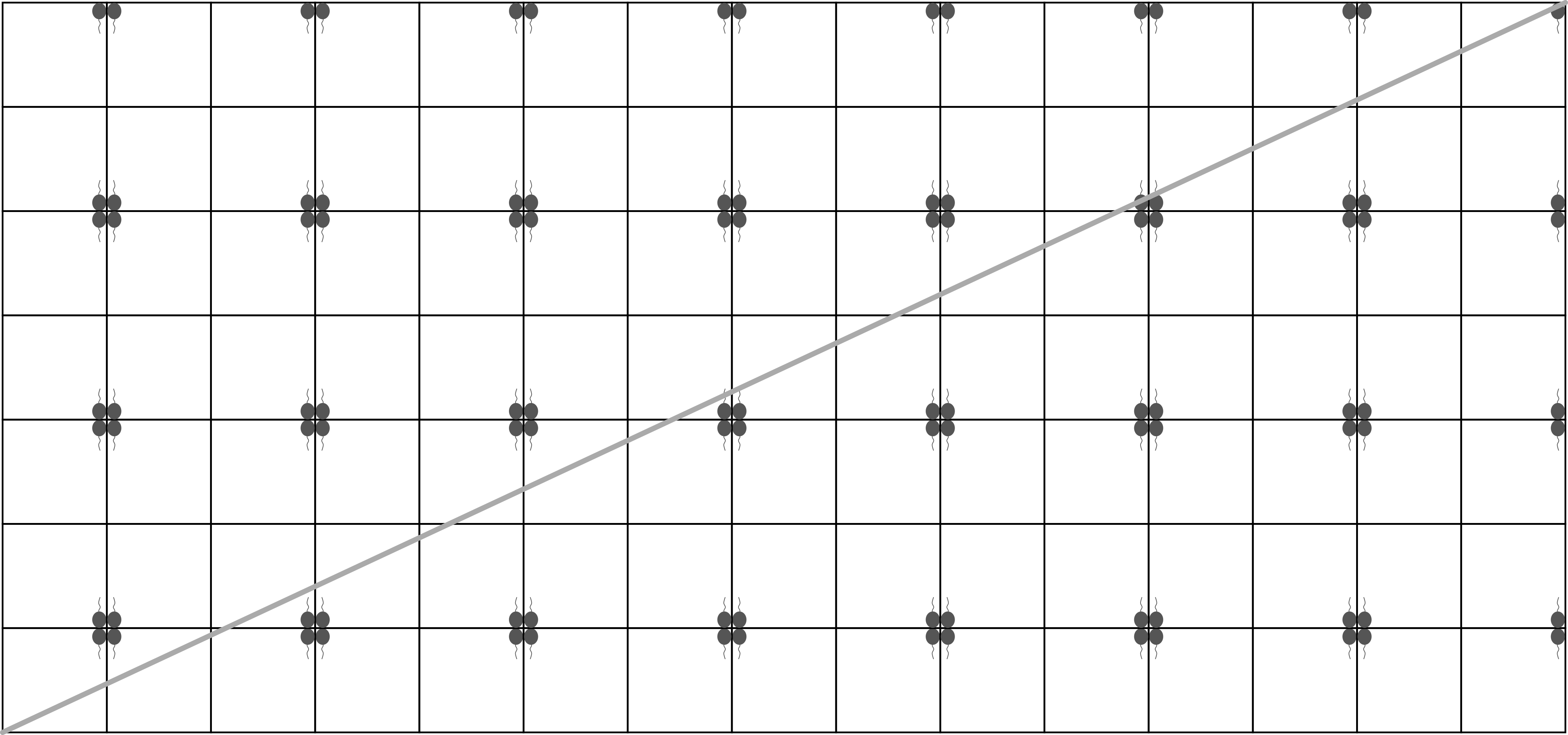
Skupovi i su nacrtani na slici ispod:

Iz slike možemo vidjeti da se skupovi i sijeku u točaka, što znači da točaka leži istovremeno u skupu i skupu .

Rezultat:

Neka se u desnoj grani nalazi otpornika, a u lijevoj grani otpornika. Trebamo izračunati . Ukupni otpor otpornika u desnoj grani je , gdje je otpor jednog otpornika. Ukupni otpor u lijevoj grani je . Tada je ukupni otpor cijelog strujnog kruga : U zadatku je zadano da je ovaj otpor puta manji od otpora otpornika u desnoj grani. Iz ovoga dobivamo jednadžbu iz koje možemo dobiti vrijednost : U desnoj se grani nalazi puta više otpornika nego u lijevoj grani.

Rezultat:

Hrvoje će uložiti rad kako bi podigao kamen mase dovoljno visoko da je cijeli kamen iznad zida. Dakle, moramo izračunati kolika je najmanja visina na koju moramo podići centar mase kamena. Težište trokuta dijeli težišnicu na dva dijela u omjeru duljina , gdje je dulji dio onaj dio bliži vrhu iz kojeg smo povukli težišnicu. U jednakostraničnom trokutu, svaka težišnica je jednake duljine kao i visina trokuta, što znači da je težišnica duljine . Dakle, udaljenost težišta od bilo koje stranica trokuta je . To znači da je težište udaljeno od bilo koje točke na stranici trokuta za bar . U trenutku kad je težište trokuta (i time centar mase kamena) direktno iznad zida, postoji točka na nekoj od stranica trokuta koja dodiruje zid. U slučaju da to nije tako, mogli bi pomaknuti cijeli kamen prema dolje i tako bi Marianne morala uložiti manji rad. Ta točka (koja dodirauje zid) je barem udaljena od centra mase kamena. To znači da ukoliko želimo podići cijeli kamen preko zida, centar mase kamena mora biti barem iznad zida. Ako se pitamo je li moguće na taj način podići kamen preko zida, vidimo da je, ukoliko je jedna od duljih strana kamena paralelna sa zidom. To znači da, kako bi podigao kamen preko zida, Hrvoje mora podići centar mase kamena za do vrha zida i onda još za kako bi cijeli kamen mogao proći preko zida. Sveukupno, mora podići centar mase kamena za , što znači da će se potencijalna energija kamena povećati za . Rad je promjena energije, što znači da rad koji Marianne izvrši je jednak potencijalnoj energiji koju kamen dobiva, dakle rad koji Marianne mora izvršiti je .

Rezultat:

Pretpostavimo da je Andrej uzeo brojeve i , onda su na ploči bili napisani i brojevi i . Kada bi jedan od njih bio nula, uzmimo , aritmetički niz bi imao brojeve , , , . i su dva uzastopna broja i trebali bi se razlikovati za . Odnosno, svi brojevi u nizu bi bili isti, stoga bi bilo . Ali ovaj slučaj se ne može dogoditi jer su i različiti brojevi. Možemo dalje pretpostaviti da s i veći od . Možemo također uzeti da je (inače bi mogli samo zamjeniti oznake od i ). S obzirom na ovo, možemo reći da je najveći broj na ploči , a drugi najveći . Kako se brojevi u aritmetičkom nizu moraju ili uvijek uvećavati ili uvijek smanjivati, a i su dva uzastopna broja u ovom nizu. Stoga se svaka dva uzastopna broja moraju razlikovati za što je jednako . Stoga treći broj u ovom nizu mora biti , broj koji je za manji od . Zadnji broj je , koji treba biti manji za od . To nam daje uvjet: Ako Andrej na početku odabere brojeve i , nakon što napiše njihov zbroj i pozitivnu razliku dobit će aritmetički niz , , , . Preostaje samo provjeriti u koliko parova i su i jednoznamenkasti brojevi. Lako se provjeri da , mogu jedino biti parovi , i . Andrej je na tri načina mogao odabrati parove brojeva.

Rezultat:

Nakon potezanja užeta, koloture koje nisu privezane za strop zajedno s pričvršćenom masom počinju se kretati prema gore. Tijekom tog procesa, dio užeta oko nepričvršćenih kolotura nestaje, dok se povećava dio koji Juraj povlači. Na slici je prikazano što se događa kada su koloture podignute od donje isprekidane linije do gornje - dio užeta jednake veličine nestaje sa svakog od pet dijelova koji se nalazi između isprekidanih linija. Prema tome, povuče li Juraj uže za određenu udaljenost, masa pričvršćena za koloture giba se prema gore za petinu te udaljenosti kako bi ukupna duljina užeta koja nestaje oko pričvršćenih kolotura bila jednaka duljini užeta koje je Juraj povukao prema sebi. Dakle, ako Juraj uže povlači konstantnom brzinom od , masa se podiže brzinom .

Rezultat:

Prisjetimo se kako računamo najmanji zajednički višekratnik i najveći zajednički djelitelj. Prvo trebamo naći rastav brojeva na proste faktore. Radimo sljedeće za svaki prosti broj: Iz toga dobijemo da mora vrijediti za sve prirode brojeve , . Oba broja i su višekratnici broja 30 pa ih možemo zapisati kao i za neke prirodne brojeve i . Stoga određivanje najvećeg zbroja od je isto kao i traženje prirodnih brojeva i za koje je zbroj najveći. Kako je 30 najveći zajednički djelitelj brojeva i , najveći zajednički djelitelj brojeva i je 1. Još znamo da vrijedi: Zbroj dva broja za koja znamo umnožak je najveći kada se brojevi razlikuju za što je više moguće. Njihova je razlika najveća ako su i (možemo i zamjeniti i ). U ovom slučaju imamo da je i da ova dva broja imaju najveći mogući zbroj . Kada to uvrstimo natrag u i dobijemo da je zbroj Tomislavovih brojeva .

Rezultat:

Pogledajmo kako djeluju sile u ovom zadatku. Na most djeluje sila teža u centru mosta s magnitudom . Osim toga, također postoji sila kojom lanci djeluju na most. Ako se most ne pomiče, ne rotira se. Uvjet za to da se most ne rotira je to da je zbroj svih momenata sila koje djeluju na njega nula. Sila teža djeluje na udaljenosti od i djeluje momentom sile . Vertikalna komponenta sile kojom lanci djeluju na most na udaljenosti od mora djelovati na most momentom sile . Dakle, magnituda te sile mora biti . Budući da su dva lanca, vertikalna komponenta sile koja djeluje na svaki je .

Znamo vertikalnu komponentu sile koja djeluje na lance. Ali kako ćemo odrediti silu u smjeru lanaca? Primijetimo da je trokut kojeg čine lanac, vrata i zid sličan onome kojeg čine , te spojnica njihovih vrhova. Dakle, omjer magnituda i je jednak omjeru visine vrata i duljine lanca. Duljinu lanca možemo izračunati pomoću Pitagorinog poučka: . Nadalje: Dakle, na svaki lanac djeluje sila:

Rezultat:

Odredimo najprije vjerojatnost da je broj znamenaka 1 u datoteci paran broj. Neka su prvih 2021 znamenaka proizvoljne. Dakle, mogu sadržavati ili paran ili neparan broj znamenki 1. Posljednja znamenka je ili 0 ili 1. Ovisno o posljednjoj znamenki, parnost broja znamenki 1 u prvih 2021 znamenki se ili promijeni ili ostaje ista. Hoće li se ili neće promijeniti ovisi samo o posljednjoj znamenci, a nju biramo nasumično s jednakom vjerojatnošću za oba izbora, dakle vjerojatnost je 0,5 da će se parnost promijeniti i 0,5 da neće.
Promotrimo sada samo one skupove znamenaka koji imaju paran broj znamenaka 1. Koliko takvih ima broj znamenaka djeljiv s 4? Ako je broj znamenaka 1 paran, moguća su dva slučaja - ili je djeljiv i s 4 ili pri dijeljenju s 4 daje ostatak 2. Razmotrimo sada 2 skupa, i . U skup stavit ćemo sve slučajeve u kojima je broj znamenaka 1 djeljiv s 4, a u skup sve slučajeve s ostatkom 2. Primjetimo da sada možemo izabrati slučaj iz skupa i zamijeniti sve znamenke 0 s znamenkama 1 i obrnuto. Ako je broj znamenki 1 u početnom slučaju bio , a broj znamenki , tada će nakon zamjene broj znamenki 1 biti , a broj znamenki 0 . Međutim, ostatak pri dijeljenju s 4 je 2. Dakle, zamijenjeni slučaj pripadat će skupu B. Ponovnom zamjenom ponovno dobivamo slučaj iz , odnosno početni slučaj. Na ovaj način možemo podijeliti slučajeve u parove, jedan iz skupa , drugi iz skupa . Svaki slučaj mora pripadati jednom paru, zato skupovi i moraju sadržavati jednako mnogo slučajeva. Ovo sada znači da od slučajeva s parno mnogo znamenaka 1, broj slučajeva s brojem znamenaka 1 djeljivim s 4 zauzima polovicu slučajeva. Dakle, vjerojatnost da je broj zapisanih znamenki 1 djeljiv s 4 je

Rezultat:

Ako jednostavno pokušamo nacrtati prvih nekoliko refleksija zrake shvatit ćemo da je potrebno relativno puno. Svaki put, moramo izračunati gdje se zraka točno reflektira, što nije toliko jednostavno. Zato, isprobat ćemo malo drugačiji pristup.

Umjesto da reflektiramo zraku preko linije okomite na zid u točki refleksije, prebacit ćemo je preko zida u koji je udarila. Pretpostavimo da je desno od naše sobe identična takva soba koja je preokrenuta tako da dijele zid. Dakle, kada zraka produži u novu sobu, putovat će jednako u njoj kao da smo ju odbili u početnoj. Slično, tako možemo nastaviti dodavati nove sobe koje će oponašati početnu sobu. Od prve refleksije, znamo kako zraka putuje desno i gore. Nakon nekog vremena, udarit će neki od kuteva pomoćnih soba, i sa malo sreće, balon će se nalaziti baš u tom kutu!

Zraka će udariti kut ako su udaljenosti proputovane udesno i gore višekratnici od . Očito će udaljenost proputovana udesno biti višekratnik, zato je dovoljno promatrati za koje će cijele brojeve također i biti cijeli broj. Kako je cijeli broj, onda najmanji takav očito mora biti . Ta situacija je skicirana ispod:

Iz ove skice možemo vidjeti da zraka zaista udara u kut s balonom. Sada samo treba pobrojati broj refleksija koje su se dogodile. Prema našem pristupu, svaki put kad smo zraku reflektirali smo ušli u novu sobu. Dakle, iz skice se vidi da je zraka prošla u novu sobu puta prije nego što je udarila balon.

Slika dolje pokazuje točno kako se zraka odbila puta:

Rezultat:

Nakon dodavanja brašna mase u čašu s površinom baze , sila teža koja djeluje na čašu se povećala za . Da bi čaša i dalje plutala, sila uzgona se morala povećati za isti iznos. Sila se uzgona mogla povećati jedino zbog povećanja dijela čaše uronjenog u vodu. Za ovu promjenu, koristimo Arhimedov princip gdje je promjena volumena uronjenog dijela čaše. Nadalje, dobivamo: Da bi se volumen uronjenog dijela povećao, dno manje čaše mora potonuti dublje i približiti se dnu veće čaše za neku visinu . Usporedno tome, čaša potiskuje volumen vode , koja se otići negdje. Otići će oko male čaše. Tamo će uzrokovati povećanje u površini vode za . Volumen vode koja je otišla sa strana male čaše je , gdje je površina baze veće čaše. Dakle, dobivamo: Visina uronjenog dijela čaše se ovim putem poveća za , te dobivamo: Kombiniranjem ovih jednadžbi dobivamo: Dakle, visina površine vode u čaši se povećala za

Rezultat:

Bilo bi teško zbrojiti toliko devetki. Stoga ćemo pokušati pronaći drugi način. Primjetimo da ako dodamo svakom broju dobit ćemo broj koji počinje s i sve ostalo ima nule. Zbroj možemo stoga zapisati kao

Kada zbrojimo sve dobijemo . Ostale pribrojnike zbrojimo u u kojem ima jedinica. Broj koji je Snježana dobila je ovaj veliki broj umanjen za .

Kako ovaj broj izgleda? Oduzimanjem utječe samo na zadjih znamenki tog velikog broja, i one postanu . Ostalih znamenki ostaju nepromijenjene. Zbroj znamenki Snježaninog zbroja je .

Rezultat:

Pretpostavimo da su dimenzije cigle , , i da joj je masa . Tada tlakove , i možemo izraziti na sljedeći način: Nakon što pomnožimo sve jednadžbe dobijemo: Međutim, je volumen cigle, pa se prethodna jednadžba može zapisati i kao: Preostalo je uočiti da je gustoća cigle . Koristeći ovo možemo naći masu cigle: Masa Bobove cigle je .

Rezultat:

Neka je P sjecište pravaca i . Budući da su pravci i usporedni, trokuti i su slični. Omjer pripadajućih stranica ovih trokuta je . Iz ovoga slijedi: Međutim, znamo i . Koristeći ove dvije jednadžbe dobijemo: U trokutu vrijedi jednakost , pa upotrebom Pitagorinog poučka zaključujemo kako se radi o pravokutnom trokutu sa pravim kutom u točki . Stoga je i trokut također pravokutan. Površina trapeza jednaka je razlici površina ovih dvaju trokuta.

Katete trokuta duge su i , pa je površina . Trokut ima katete duljina i , pa mu je površina .

Stoga je površina trapeza jednaka .

Rezultat:

Riješimo lakši problem, u kojem je Tez označila samo točke, prvo. Označimo ih sa , , i tako da one po redu leže na krugu. Nacrtani segmenti ne smiju imati zajedničke točke, uključujući i krajnje točke.

Dakle, jedan segment mora imati krajnje točke u jednom paru označenih točaka, a drugi segment u drugom paru točaka. Zbog navedenoga se dva segmenta mogu nacrtati na tri načina:

1. segment a ,

2. segment a ,

3. segment a .

U drugom slučaju, segmenti se presjeku, dok u ostalima ne. Zbog toga, u slučaju kada imamo točke, imamo 2 načina da nacrtamo segmente. Sada se možemo vratiti problemu zadatka, u kojem Tez ima točaka i krug. Krajnje točke parova segmenata nalazit će se u različite točke. Nakon odabira tih točaka, primijenimo što smo saznali iz problema sa točke. Nadalje, nakon izabranih točaka, imati ćemom načina za nacrtati segmente.

Preostaje nam izračunati broj načina na koji možemo izabrati točke. Za prvu točku imamo opcija, za drugu , za treću i za posljednju opcija.

Čineći to, uključili smo svaku četvorku u broj načina više puta. Točnije, uključili smo ga jednom za svaki mogući redoslijed bodova u njemu.

Za prvu poziciju, od svih, imamo mpgućnosti, za drugu , za treću i za zadnju . Broj načina na koji možemo izabrati 4 točke je onda . Zajedno sa činjenicom da za svaku četvorku točaka imamo načina da nacrtamo segmente, dobijemo da Tez može nacrtati segmente na načina.

Rezultat:

Označimo mase kvadara sa , , i koeficijent trenja sa . Pogledajmo kako odgovarajuće sile djeluju na odgovarajuće kvadre. Ponašaju se kao na navedenim skicama:

Sile , i su gravitacijske sile koje djeluju na kvadre. Kako svaki od gornja dva kvadra djeluje sa silom na kvadar ispod njega, nastaju normalne sile i . Najgornji kvadar djeluje silom jačine na srednji kvadar te je ona orijentirana prema dolje. U isto vrijeme, zbog akcije i reakcije, srednji kvadar djeluje silom istog iznosa, ali suprotnog smjera na njemu gornji kavadar. Nadalje, srednji i njemu donji kvadar međudjeluju silom iznosa . Sile koje djeluju u horizontalnom smjeru su sile , kojom Majo djeluje na najdonji kvadar, te sile i , koje djeluju zbog napetosti užeta. Napokon, zadnje sile su sile trenja. Na najgornji kvadar, kojeg bi htjeli pomaknuti udesno, djeluje sila ulijevo. Opet, iz akcije i reakcije, srednji kvadar mora djelovati na njemu gornji sa silom jačine . Sile trenja na srednji i njemu donji kvadar djeluju slično. Također, tlo djeluje na najdonji kvadar sa silom trenja .

Da bi naš sustav bio u mirovanju, rezultanta navedenih sila mora biti jednaka nula u svim dimenzijama. Za vertikalne sile dobivamo jednadžbe: Dok u horiznotalnom smjeru dobijemo: Gravitacijske sile se mogu izračunati iz relacije , gdje je gravitacijska akceleracija. Kada Majo djeluje maksimalnom mogućom silom, sile trenja također moraju biti maksimalne - vrijedi da kada bi Majo djelovao malo većom silom, cijeli bi se sustav pomaknuo te bi jačina sile trenja bila maksimalna. Iznos navedenih sila možemo dobiti iz jednadžbe . Ostaje nam izraziti nepoznate veličine pomoću prethodnih šest jednadžbi, od kojih dobijemo: Dakle, maksimalna sila, kojom Majo može djelovati, iznosi: