Problem statements

Rezultat:

$27$

Kada Anamarija da Boži $11$ svojih kamenčića, ona gubi $11$ kamenčića, a Božo dobiva $11$ kamenčića. Dakle, razlika u broju kamenčića se mijenja za $11+11=22$. Stoga, Anamarija će sada imati $49-22$ kamenčića nego Božo.

Rezultat:

$5$

Prva tri mjeseca $2023.$ su imali $31$, $28$ odnosno $31$ dan. Zajedno čine $31+28+31=90$ dana, što je $90\cdot 24=2160$ sati. Kleopatra je tako prešla $10800$ kilometara u $2160$ sati. Stoga je njezina prosječna brzina morala biti $\frac{10800\mathrm{km}}{2160h}=5\mathrm{km}∕h$.

Rezultat:

$56$

Kako bi nacrtala donja četiri kvadrata, Laura treba nacrtati $13$ dužina. Kako bi dodala tri kvadrata crta dodatnih $7$ dužina. Za iduća dva kvadrata crta još $5$ dužina. Konačno, za kvadrat na vrhu, Laura nacrta $3$ dužine. Ukupno, nacrtala je $13+7+5+3=28$ dužina. Svaka je duljine $2\mathrm{cm}$, pa je ukupna duljina svih dužina jednaka $28\cdot 2\mathrm{cm}=56\mathrm{cm}$.

Rezultat:

$45$

Uz pretvorbe dane u formulama, odredimo da je $36\mathrm{oz}$ upravo $1l$. Dakle, volumen soka u litrama je $\frac{12\mathrm{oz}}{36\mathrm{oz}∕l}=\frac{1}{3}l$. Stoga, sok sadrži $3\cdot 150=450$ kilokalorija po litri, odnosno $450:10=45$ kilokalorija u $100\mathrm{ml}$.

Rezultat:

$7$

Kad bi škrinja imala $48$ novčića manje, svaki gusar bi dobio $6$ novčića manje nego što trenutno ima. Dakle, mora biti $48:6=8$ gusara. Budući da je pitanje koliko Jan ima prijatelja gusara, točan odgovor je $8-1=7$.

Rezultat:

$4620$

U $18$ minuta Sandra otrči $18:3=6$ krugova. Svaki njezin krug ima duljinu od $2\pi \cdot 70m=140\pi m$. Dakle, ona prijeđe udaljenost od $6\cdot 140\pi m=840\pi m$ i isti taj broj koraka. Slično, Blanka otrči $18:2=9$ krugova duljine $2\pi \cdot 35m=70\pi m$. Ona prijeđe $9\cdot 70\pi m=630\pi m$ i isti taj broj koraka. Dakle, zajedno naprave $840\pi +630\pi =1470\pi$ koraka. Ako koristimo aproksimaciju $\pi =\frac{22}{7}$, dobivamo da su napravile $1470\cdot \frac{22}{7}=4620$ koraka.

Ako koristimo vrijednost $\pi =3,14$, dobit ćemo kao rezultat $4615,8$, što će nam dati isto rješenje nakon zaokruživanja na najbližu deseticu.

Rezultat:

$9$

Za otvoriti vrata uz minimalnu silu, trebamo postići ravnotežu momenta sile na krajevima poluge. Moment sile $M$ zatvarača jednak je sili pomnoženoj s udaljenošću od šarki $M=48N\cdot 15\mathrm{cm}=720N\mathrm{cm}$. Koristeći istu jednadžbu, dobivamo da je sila potreba za otvoriti vrata s udaljenosti $a=80\mathrm{cm}$:

Rezultat:

$6,28$

Uz pretpostavku da je Zemlja savršena kugla, uže omotano oko ekvatora opisat će kružnicu. Označimo li radijus te kružnice s $r$, Evino će uže biti duljine $2\mathit{\pi r}$. S druge strane, Adamovo će uže činiti kružnicu radijusa $r+1m$, stoga mora biti duljine $2\pi (r+1m)$. Razlika u duljinama dvaju užeta je $2\pi (r+1m)-2\mathit{\pi r}=2\pi m\doteq 6,28m$.

Rezultat:

$5$

Svaki put kada svjetlosna zraka udari u zrcalo, ona mijenja svoj smjer za $90^{\circ }$ udesno ili ulijevo (ovisno o orijentaciji zrcala). Lako je pronaći konfiguraciju zrcala gdje je potrebno samo $5$ refleksija (orijentacija zrcala u praznim kvadratima nije bitna):

S druge strane, lako se vidi da nije moguće imati najkraću rutu kroz $3$ kvadratića (zraka ne bi promijenila smjer u nekoliko kvadrata). Nadalje, vidi se da broj refleksija mora biti neparan - nakon svake neparne refleksije, zraka nastavlja vertikalno (nakon parne nastavlja horizontalno).

Dakle broj refleksija je neparan broj veći od $3$ pa je jasno da je $5$ najmanji takav broj.

Rezultat:

$45$

Koristimo li samo znamenku $1$, imamo $5$ čupavih brojeva u danom rasponu, i to $11$, $111$, $1111$, $11111$ i $111111$. Slično, imamo po $5$ čupavih brojeva za svaku od znamenki od $2$ do $9$, a za znamenku $0$ nemamo čupavih brojeva. Stoga imamo $9\cdot 5=45$ čupavih brojeva većih od deset i manjih od milijun.

Rezultat:

$1$

Zbroj svih brojeva upisanih na ploči je $0+1+2+3+4+5+6=21$. To znači da zbroj brojeva u svakom stupcu treba biti $21:3=7$. Tada broj $0$ ne može biti u prvom ni zadnjem stupcu jer bismo u drugi kvadratić trebali upisati broj $7$, ali taj broj ne smijemo koristiti. Dakle, $0$ upisujemo u srednji stupac, zbog čega će umnožak u srednjem stupcu uvijek biti $0$. Stoga Danijel može dobiti samo $1$ rezultat, a to je $0$.

Rezultat:

$250$

Da Dorijan nije zaboravio zatvoriti odvod, kada bi se napunila u vremenu $150l:0,2l∕s=750s$. No, Dorijan je zaboravio zatvoriti odvod, što je smanjilo dotok vode na $0,2l∕s-0,05l∕s=0,15l∕s$. Sada će se kada napuniti za $150l:0,15l∕s=1000s$, pa će punjenje kade trajati $1000s-750s=250s$ dulje.

Rezultat:

$16$

Nakon prvog poteza, kralj se može pomaknuti na bilo koje polje prikazano na ovoj slici:

Sada je pitanje, na koliko polja se kralj može pomaknuti iz bilo koje pozicije s prethodne slike. Lako vidimo da se kralj može pomaknuti na bilo koje od ovih $16$ polja.

Rezultat:

$14$

Dva nova trokuta imaju po dvije stranice iste kao stranice izvornog četverokuta i jednu stranicu duljine dijagonale. To znači da je novi opseg jednak zbroju opsega uvećanom za dvostruku duljinu dijagonale. Budući da se opseg povećao za $77\mathrm{cm}-49\mathrm{cm}=28\mathrm{cm}$, duljina dijagonale je $28\mathrm{cm}:2=14\mathrm{cm}$.

Rezultat:

$10$

Nakon bacanja, horizontalna komponenta brzine lopte bit će $9\mathrm{km}∕h=2,5m∕s$, a Sarina će nova brzina biti $18\mathrm{km}∕h=5m∕s$. Dakle, relativna brzina između Sare i lopte bit će $5m∕s-2,5m∕s=2,5m∕s$. Stoga će, nakon $4$ sekunde kada lopta padne na tlo, Sara od nje biti udaljena $2,5m∕s\cdot 4s=10m$.

Rezultat:

CDAB

U prvom koraku određujemo Aninu poziciju. Budući da su sve tvrdnje lažne, Ana nije mogla doći druga. Branka i Cvjeta su došle nakon i prije Ane, tim redom. Dakle, barem je jedna djevojka stigla prije Ane i barem jedna nakon Ane, pa nije moguće da je Ana stigla prva ili zadnja. Ostaje samo mogućnost da je treća. Brankina lažna tvrdnja da je stigla prije Ane implicira da je stigla nakon nje, pa je Branka zadnja. Dina nije došla prva, dakle došla je druga jer smo već popunili treće i četvrto mjesto. Na kraju, Cvjeta je mogla doći samo prva, a to je u skladu s negacijom njezine tvrdnje. Proredak je CDAB.

Rezultat:

$5$

Izračunajmo interval tramvaja $12$. Kad se Jakov vozi u tramvaju, njegova relativna brzina prema suprotnim tramvajima je dvostruko veća od stvarne brzine tih tramvaja. To znači da konstantnu udaljenost između dva uzastopna tramvaja prijeđe dvostruko brže. Dakle, pravi interval pristizanja na stanicu je dvostruko dulji nego što se čini Jakovu kad gleda tramvaje iz suprotnog smjera. Tramvaj $12$ staje na stanici svake $2\cdot 2=4$ minute. Po satu je to $60:4=15$ tramvaja broj $12$.

Slično, tramvaja broj $5$ po satu staje $60:6=10$. Dakle, na stanici u satu staje $15-10=5$ tramvaja $12$ više nego tramvaja $5$.

Rezultat:

$250$

Moramo razmisliti kako trenje utječe na kutiju. Sila trenja djeluje samo između čvrstih tijela koja međusobno na sebe djeluju nekom silom pritiska. No, u našem slučaju kutija ne uzrokuje nikakav pritisak na okomiti zid. Dakle, na kutiju ne djeluje sila trenja. To znači da je jedina sila (osim one od Boba) koja djeluje na kutiju gravitacijska sila $F_g=\mathit{mg}$, gdje je $m=25\mathrm{kg}$ masa kutije. Bob mora djelovati silom $F$ istog iznosa, pa mora vući uže silom $F=\mathit{mg}=25\mathrm{kg}\cdot 10N∕\mathrm{kg}=250N$.

Rezultat:

$50$

Karolinini zahtjevi su da uzme barem $2$ pekmeza od maline, $5$ od borovnice, $1$ od kupine, $1$ od brusnice i $1$ pekmez od jagode. Razmotrimo što bi se moglo dogoditi kad se neki od ovih zahtjeva ne bi ispunio. Najgori slučaj koji se mogao dogoditi zbog čega Karolina ne bi imala $2$ pekmeza od maline je da je uzela sve pekmeze drugih vrsta i $1$ pekmez od maline. Ukupno je to $1+15+7+15+9=47$ pekmeza. Međutim, da je uzela $48$ pekmeza, taj problem se ne bi dogodio. Slično, problem bi bio da je uzela $4$ pekmeza od borovnice i sve pekmeze ostalih vrsta - ukupno $10+4+7+15+9=45$ pekmeza. Dakle, treba uzeti barem $46$ pekmeza. Ponavljajući istu ideju za kupine, brusnice i jagode, nema problema ako Karolina uzme redom barem $(10+15+0+15+9)+1=50$, $(10+15+7+0+9)+1=42$ ili $(10+15+7+15+0)+1=48$ pekmeza. Spojimo li sve, saznajemo da će svi zahtjevi biti ispunjeni ako je broj uzetih pekmeza najveći od brojeva $48$, $46$, $50$, $42$, $48$. Stoga Karolina mora uzeti $50$ pekmeza.

Rezultat:

$64$

Neka je $s$ ukupna duljina staze i $t$ vrijeme koje je trebalo pobjedniku da dođe do cilja. Znamo da je prosječna brzina pobjednika $24\mathrm{km}∕h$ pa je $\frac{s}{t}=24\mathrm{km}∕h$.

Dvije trećine staze čine nizbrdice, što znači da je duljina nizbrdica ukupno $\frac{2}{3}s$. Nadalje, pobjednik je na uzbrdice potrošio $3$ puta više više vremena, iz čega slijedi da je na nizbrdice potrošio $\frac{1}{4}t$. Prosječna je brzina na nizbrdicama:

Uvrštavanjem $\frac{s}{t}=24\mathrm{km}∕h$ dobivamo da je prosječna brzina pobjednika na nizbrdicama:

Rezultat:

$95$

Pogledajmo zadnji redak i drugi stupac. Oni trebaju imati jednak zbroj, ali imaju jedno zajedničko polje. Dakle, i zbrojevi preostalih polja koja nisu zajednička isto trebaju biti jednaki. Stoga zbroj brojeva $15$ i $19$ mora biti isti kao zbroj broja $16$ i broja u srednjem polju. Ovaj zbroj je $15+19=34$, tako da broj u srednjem kvadratu mora biti $34-16=18$.

Sada imamo sve brojeve na jednoj od dijagonala. Dakle, zbroj brojeva u svakom retku, stupcu i na obje dijagonale mora biti $17+18+19=54$. Lako sada popunimo cijelu tablicu.

Na kraju izračunamo da je zbroj brojeva koji nedostaju $21+22+18+14+20=95$.

Rezultat:

$0,8$

Možemo zamijeniti svaki $1m$ žice s otpornikom otpora $R_0=0,1\mathrm{\Omega }$. Na taj način dobivamo sljedeći dijagram:

Sad koristeći uobičajene formule za otpornike u serijskom i paralelnom spoju nalazimo da je otpor između vrhova $A$ i $B$:

Rezultat:

$5$

Voda volumena $V=150\mathrm{hl}$ ima masu $m=V{\rho }_{\mathit{voda}}$. Da bismo ju zagrijali s $t_1=29\circ C$ na $t_2=33\circ C$ trebamo toplinu $Q=c_{\mathit{voda}}m(t_2-t_1)=c_{\mathit{voda}}V{\rho }_{\mathit{voda}}(t_2-t_1)$. Ova toplina mora biti jednaka radu koji izvrše solarni paneli. Oni imaju snagu $P_0=1,4\mathrm{kW}∕m^2$ po jedinici površine, stoga paneli, kako je ukupna površina $S$, imaju snagu $P=P_{0}S$. Nakon $t=10h$, izvršit će rad $W=\mathit{Pt}=P_0\mathit{St}$, a to je rad izvršen na vodi, pa imamo:

Dakle, Ana treba $5m^2$ solarnih panela.

Rezultat:

$40$

Označimo poredak golova kao niz slova F i M, gdje F označava pogodak fizičara, a M pogodak matematičara. Uz ovu notaciju, vidimo da postoji $10$ mogućih redoslijeda postizanja pogodaka u prvom poluvremenu: MMFFF, MFMFF, MFFMF, MFFFM, FMMFF, FMFMF, FMFFM, FFMMF, FFMFM, FFFMM. Slično vidimo da su golovi u drugom poluvremenu mogli biti raspoređeni na $4$ načina: FMMM, MFMM, MMFM, MMMF. Prvo i drugo poluvrijeme su nezavisni pa bilo koji poredak prvog poluvremena može biti sparen s bilo kojim poretkom drugog poluvremena. Dakle, ukupni broj mogućnosti je $10\cdot 4=40$.

Rezultat:

$125$

Kako robot svaku stranu gura silom $F$, sila trenja sa svake strane je $F_f=\mathit{fF}$ i usmjerena je prema gore, gdje je $f$ koeficijent trenja $f=0,3$. S druge strane, sila teža $F_g=\mathit{mg}$ djeluje na robota prema dolje. Kako bi robot ostao stabilan, sila teža mora biti jednaka zbroju sve četiri sile trenja. Dakle:

Konačno, sila $F$ je:

Rezultat:

$3$

Svaki šesterokut možemo podijeliti na $6$ jednakostraničnih trokuta. Tako preko slike možemo nacrtati mrežu trokuta:

Odavde odmah vidimo da je duljina stranice šesterokuta (koja je jednaka duljini stranice trokuta) $12\mathrm{cm}:4=3\mathrm{cm}$.

Rezultat:

$1100$

Brod će potonuti kada se gravitacijska sila izjednači sa silom uzgona. Maksimalna sila uzgona koja može djelovati na brod volumena $V$ je $F_{\mathit{uzg}}=V{\rho }_{\mathit{voda}}g$. Gravitacijsku silu ćemo podijeliti u ovisnosti o tome djeluje li na sami brod ili na vodu koja u brod navire. Gravitacijska sila na sami brod iznosi $F_{g_1}=\mathit{mg}$. Voda navire u brod tokom $Q$, pa će nakon vremena $t$ u brodu biti volumen vode jednak $V^{\prime }=\mathit{Qt}$. Gravitacijska sila na tu vodu bit će $F_{g_2}=\mathit{Qt}{\rho }_{\mathit{voda}}g$. Uvjet za poniranje broda je $F_{\mathit{uzg}}=F_{g_1}+F_{g_2}$, odakle možemo dobiti da je vrijeme $t$:

Dakle, brod će potonuti nakon vremena:

Rezultat:

$1990$

Obje su djevojke zbrajale godine počevši od onih u kojima su rođene do 2023. Ena je dobila veći rezultat, dakle ona je u svoju sumu dodala neke godine koje Ana nije. Kako svaki pribrojnik iznosi otprilike $2000$, broj pribrojnika koji je dodala samo Ena je $19945:2000\doteq 10$. To znači da su brojevi koje je dodala samo Ena redom $x$, $x+1$, …, $x+9$, pri čemu je $x$ godina rođenja Ene. Njihova je suma $10x+45$. Ovime smo dobili jednadžbu $10x+45=19945$ iz čega zaključujemo da je Ena rođena godine $x=\frac{19945-45}{10}=1990$.

Rezultat:

$11$

Isprobavamo mogućnosti na temelju orijentacije prvog i posljednjeg zrcala. Na temelju njih dobivamo retke sljedećih slike (radi boljeg uvida ne crtamo zrake i zrcala čija orijentacija nije bitna):

Dakle, vidimo da postoji $1+3+3+4=11$ mogućih putanja svjetlosne zrake.

Rezultat:

$\frac{68}{3}$

Neka su duljine stranica pravokutnika $\mathit{ABCD}$ $\mathit{AB}=9x$ i $\mathit{BC}=8x$ za neki $x$.

Najprije izračunamo opseg četverokuta $\mathit{ABEF}$. Katete u pravokutnom trokutu $\mathit{ECF}$ imaju duljine $4x$ i $3x$. Dakle, Pitagorin poučak daje $\mathit{EF}=\sqrt{{(4x)}^2+{(3x)}^2}=5x$. Slično, pravokutni trokut $\mathit{FDA}$ ima katete duljina $6x$ i $8x$, pa je $\mathit{FA}=\sqrt{{(6x)}^2+{(8x)}^2}=10x$. Prema tome, opseg četverokuta je $9x+4x+5x+10x=28x$.

Sada izračunajmo površinu četverokuta $\mathit{ABEF}$. Pravokutni trokuti $\mathit{ECF}$ i $\mathit{FDA}$ imaju površine $\frac{(4x)\cdot (3x)}{2}=6x^2$ i $\frac{(6x)\cdot (8x)}{2}=24x^2$. Površina pravokutnika $\mathit{ABCD}$ je $(9x)\cdot (8x)=72x^2$, pa je površina četverokuta $\mathit{ABEF}$ $72x^2-6x^2-24x^2=42x^2$. Znamo da su brojčane vrijednosti opsega i površine četverokuta $\mathit{ABEF}$ iste, što znači:

Preostaje izračunati opseg pravokutnika $\mathit{ABCD}$ koji je $9x+8x+9x+8x=34x=34\cdot \frac{2}{3}\mathrm{cm}=\frac{68}{3}\mathrm{cm}$.

Rezultat:

$2$

Rad koji crv mora obaviti bit će jednak maksimalnoj potencijalnoj energiji crva tijekom njegovog penjanja preko kocke (s pretpostavkom da je njegova potencijalna energija na početku bila jednaka nuli). Nije teško za vidjeti da će taj maksimum biti postignut točno u trenutku kad će crv biti u poziciji prikazanoj na slici (što je veći dio crva više, to mu je veća potencijalna energija).

"Razdijelimo" crva na 3 dijela- dva vertikalna i jedan horizontalni kao na slici. Svi će oni biti duljine $10\mathrm{cm}$, što je trećina duljine crva. Kako je on homogen, sva $3$ dijela imaju masu $m_0=3g:3=1g$. Horizontalni dio ima težište na visini $h_2=10\mathrm{cm}$, pa je potencijalna energija tog dijela jednaka $E_2=m_{0}g{h}_2=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,1m=0,001J=1\mathrm{mJ}$. Vertikalni dijelovi imaju svoja težišta na visini $h_1=h_3=5\mathrm{cm}$, pa je njihova potencijalna energija jednaka $E_1=E_3=m_{0}g{h}_1=m_{0}g{h}_3=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,05m=0,0005J=0,5\mathrm{mJ}$.

Dakle, makismalna potencijalna energija na crva bit će $E=E_1+E_2+E_3=0,5\mathrm{mJ}+1\mathrm{mJ}+0,5\mathrm{mJ}=2\mathrm{mJ}$, što je jednako radu potrebnom za penjanje.

Rezultat:

$1050$

Problem možemo podijeliti na manje, lakše dijelove. Prvo, koliko pokušaja trebamo da dođemo do ABA? Budući da u engleskoj abecedi ima $26$ slova, bit će potrebno $26$ ponavljanja za promjenu posljednjeg slova. Koliko za BAA? Pa, za svakih $26$ ponavljanja posljednjeg slova, drugo slovo će se povećati za $1$, prema tome, da bismo došli do BAA od AAA, potrebno nam je $26\cdot 26=676$ pokušaja. Sada da bismo došli do BOA od BAA potrebno nam je $26\cdot 14=364$ pokušaja jer je O $15$-to slovo abecede i moramo isprobati svih 14 slova prije njega. Konačno, $J$ je $10$-to slovo, stoga nam treba dodatnih $10$ pokušaja da dođemo do BOJ-a od BOA. To sve zajedno čini $676+364+10=1050$ pokušaja.

Rezultat:

$125$

Mehanizam ostaje mirovati samo ako je moment sile koji djeluje na svaku polugu 0. Moramo, stoga, promotriti momente sile koji djeluju na poluge. U tu svrhu najprije moramo razumjeti užad. U svakom užetu postoji napetost pa će uže djelovati na obje poluge silom iznosa jednakog toj sili napetosti. Na primjer, uže koje spaja srednju i desnu polugu djelovat će jednakom silom na srednju polugu (u desno) i desnu polugu (u lijevo). Štoviše, te sile djeluju na istoj visini, zato i na jednakoj udaljenosti od osi rotacije poluga. Zaključujemo da svako uže na obje poluge djeluje momentom sile jednakog iznosa.

To znači da možemo ignorirati srednju polugu. Uistinu, sila koja djeluje na desnu polugu uzrokuje na njoj moment sile iznosa $M$. To treba kompenzirati momentom sile koje stvara napetost užeta pričvršćenog za desnu polugu. Budući da užad nosi moment sile, iznos momenta kojim desno uže djeluje na srednju polugu mora također biti $M$. Slično, kada raspišemo silu napetosti lijevog užeta, dobivamo da je moment sile na lijevu polugu ponovo $M$.

Dakle, kako bi mehanizam ostao mirovati, dvije relevantna sile moraju imati moment sile istog iznosa, što daje jednadžbu:

Patrik mora povuči polugu silom od $125N$.

Rezultat:

$2,15$

Neka duljine i nazivi vrhova budu kao na ovoj slici:

Promotrimo pravokutne trokute $\mathit{ABP}$ i $\mathit{ACP}$. Možemo za njih napisati kako glasi Pitagorin poučak te dobivamo:

Ako izrazimo $h^2$ iz obje jednakosti i usporedimo ih, dobivamo:

Sada možemo primijeniti formulu $a^2-b^2=(a-b)(a+b)$ na obje strane kako bismo dobili:

Ali znamo da je $y+x=20\mathrm{cm}$. Dakle, razlika duljina $y-x$ koju trebamo pronaći je:

Rezultat:

$75$

Neka je $m$ masa vagona, $r=30m$ radijus petlje i $v$ brzina vagona u najvišoj točki petlje.

Iz prvog dijela zadatke znamo da u najvišoj točki petlje na vagon mora djelovati centripetalna sila $F_c=\frac{m{v}^2}{r}$. Dvije sile mogu na taj način i u pravom smjeru djelovati na vagon - gravitacijska sila $F_g=\mathit{mg}$ i neka sila podloge kojom djeluju tračnice petlje. Želimo da centripetalna sila bude što manja (za veću centripetalnu silu vagon će trebati veću brzinu, što znači više energije na početku). Budući da se ne možemo riješiti gravitacijske sile, minimalna je upravo sila $F_c=F_g$. Odavde dobivamo:

Promotrimo sada energije. Na početku vagon ima samo potencijalnu energiju $E_1=\mathit{mgh}$. Međutim, na vrhu petlje vagon ima i potencijalnu i kinetičku energiju. U najvišoj točki nalazit će se na visini $2r$ i imati brzinu $v$ pa će mu energija biti $E_2=\mathit{mg}(2r)+\frac{1}{2}m{v}^2$. Kako je energija sačuvana, $E_1=E_2$. U kombinaciji s jednadžbom za $v^2$ dobivamo:

Stoga bi kolica trebala početi padati s visine $h=\frac{5}{2}r=\frac{5}{2}\cdot 30m=75m$.

Rezultat:

$23$

Rješenje se prirodno dijeli na dva dijela. Najprije pokazujemo da su mogle biti odigrane $23$ partije. Nakon toga, pokazujemo da bi postojala skupina natjecatelja iz teksta zadatka ukoliko je odigrano $24$ partija. To će dokazati da je odgovor $23$.

Prvi dio. Označimo natjecatelje brojevima $1$, $2$, …, $24$. Neka su odigrane partije između natjecatelja $1$ i $2$, $2$ i $3$, …, $23$ i $24$. Odaberemo li bilo koju skupinu natjecatelja, u njoj uvijek postoji natjecatelj s najmanjim brojem - nazovimo ga $P$. U toj skupini, natjecatelj $P$ mogao je odigrati partiju samo s natjecateljem $P+1$, s obzirom da $P-1$ ne može biti član skupine (u tom bi slučaju on bio natjecatelj s najmanjim brojem). Prema tome, natjecatelj $P$ odigrao je partiju s najviše $1$ osobom iz skupine. Budući da to vrijedi za proizvoljnu skupinu natjecatelja, ne postoji skupina koja zadovoljava uvjet iz teksta zadatka. Dakle, mogle su se odigrati $23$ partije.

Drugi dio. Dokažimo da, ukoliko su odigrane $24$ partije, uvijek postoji skupina natjecatelja sa svojstvom iz teksta zadatka. Ukoliko postoji neki par igrača koji su odigrali barem dvije partije međusobno, oni trivijalno tvore traženu skupinu. Dakle, možemo pretpostaviti da ne postoji takav par.

Pretpostavimo najprije da je svaki natjecatelj odigrao barem dvije partije. Odaberimo natjecatelje na sljedeći način. Počnimo s proizvoljnim natjecateljem $P_0$. On je odigrao partiju s natjecateljem $P_1$. $P_1$ je odigrao s barem dva natjecatelja, stoga postoji $P_2\ne P_0$ koji je s njime odigrao partiju. Slično, pronađimo $P_3\ne P_1$ s kojim je partiju odigrao $P_2$. Nastavimo na isti način, sve dok u nekom trenutku ne dođemo do natjecatelja koji je već na neki način označen. Sada imamo skup natjecatelja $P_k$, $P_{k+1}$, …, $P_n$ sa svojstvom da je $P_i$ igrao protiv $P_{i-1}$ i $P_{i+1}$, dok su $P_k$ i $P_n$ igrali međusobno. Drugim riječima, možemo ih posložiti u krug navedenim redoslijedom tako da je svaki igrao sa svojim susjedima. To dokazuje da takva skupina ima svojstvo iz zadatka. Dakle, ukoliko je svaki natjecatelj odigrao barem dvije partije, gotovi smo.

Preostaje provjeriti slučaj kad je netko odigrao manje od dvije partije. Tada možemo zanemariti tog natjecatelja te ostajemo s manjim ukupnim brojem natjecatelja. Ipak, broj partija odigranih u preostalom skupu natjecatelja svakako je veći ili jednak broju natjecatelja. Dakle, nakon zanemarivanja natjecatelja preostaju dvije mogućnosti: ili su svi preostali natjecatelji odigrali barem dvije partije, ili postoji natjecatelj koji je odigrao jednu ili nijednu. U prvom slučaju prethodni argument pokazuje da postoji skupina natjecatelja sa svojstvom iz teksta zadataka. U suprotnom, postoji još jedan natjecatelj kojega zanemarujemo. Nastavljamo postupak. Ukoliko možemo neprestano smanjivati broj natjecatelja, nakon dovoljno ponavljanja (točnije 21 ponavljanje) ovog postupka, dolazimo do tri natjecatelja koji su međusobno odigrali barem tri partije. Jedina je mogućnost da su odigrali jedan protiv drugoga, tako da njih troje formiraju skupinu koju pokušavamo pronaći.

Ovime smo dokazali da tražena skupina postoji ukoliko su odigrane $24$ partije.

Iz svega navedenog zaključujemo da je najveći mogući broj odigranih partija do tog trenutka $23$.

Rezultat:

$25$

Prvo trebamo otkriti pravilo o djeljivosti sa $125$. Kriterij je da posljednje $3$ znamenke broja moraju biti djeljive sa $125$ (ovo je slično kriterijima o djeljivosti sa $2$, $4$, $8$, $16$ …, ali s $5$, $25$ , $125$ …). Zašto? Zapišimo bilo koji broj kao $1000A+B$, gdje je $B<1000$. Dakle, $B$ je broj sastavljen od posljednje $3$ znamenke. Primijetimo da je $1000$ djeljiv sa $125$ jer je $1000=8\cdot 125$. Dakle, da bi broj $1000A+B$ bio djeljiv sa $125$, $B$ mora biti djeljiv sa $125$. Ovime smo dokazali kriterij djeljivosti.

Sada pogledajmo kakve to posljedice ima. Jedini brojevi s najviše $3$ znamenke djeljivi sa $125$ su $0$, $125$, $250$, $375$, $500$, $625$, $750$ i $875$. Nijedan od njih ne počinje znamenkom $4$. Stoga zaključujemo da višekratnici od $125$ ne mogu imati znamenku $4$ kao stoticu.

Konačno, vratimo se našem izvornom problemu. Znamo da je znamenka stotica $4$, tako da Lucijin rezultat ne može biti višekratnik od $125$. Da nije izostavila nijedan broj, konačni umnožak bio bi djeljiv s $5\cdot 15\cdot 25$. Dakle, rastav umnoška na proste faktore sadržavao bi broj $5$ četiri puta. Dakle, moramo ukloniti $5$ najmanje dva puta, ali tako da izostavimo samo jedan broj. To je moguće samo izostavljanjem broja $25$. To znači da je Lucija izostavila broj $25$.

Rezultat:

$28$

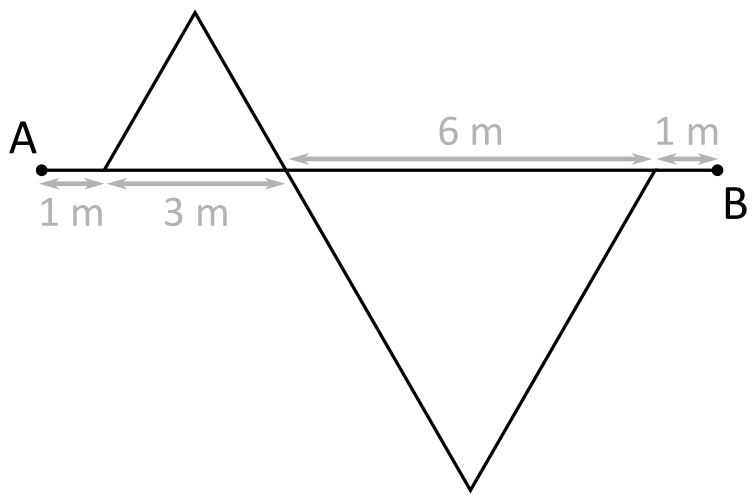
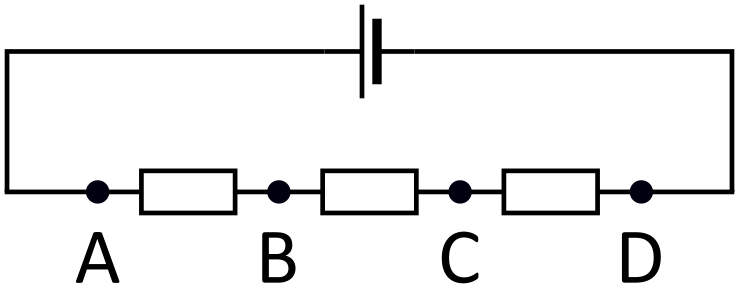
Napon između dvije točke opisuje razliku iznosa potencijala tih dviju točaka. Potencijal opisuje (električnu) potencijalnu energiju čestice naboja $1C$. U svakoj od točaka $A$, $B$, $C$ i $D$, ta bi čestica imala neku potencijalnu energiju pa taj broj možemo pridružiti svakoj od ovih točaka. Tada naponi opisuju razlike između tih brojeva.

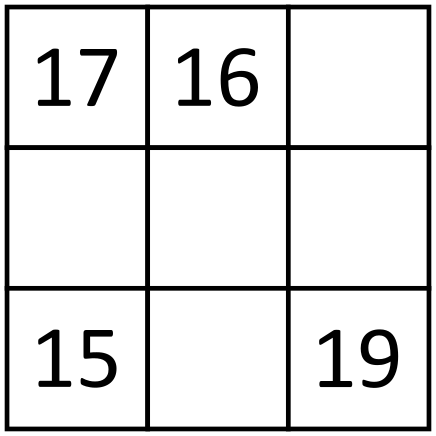
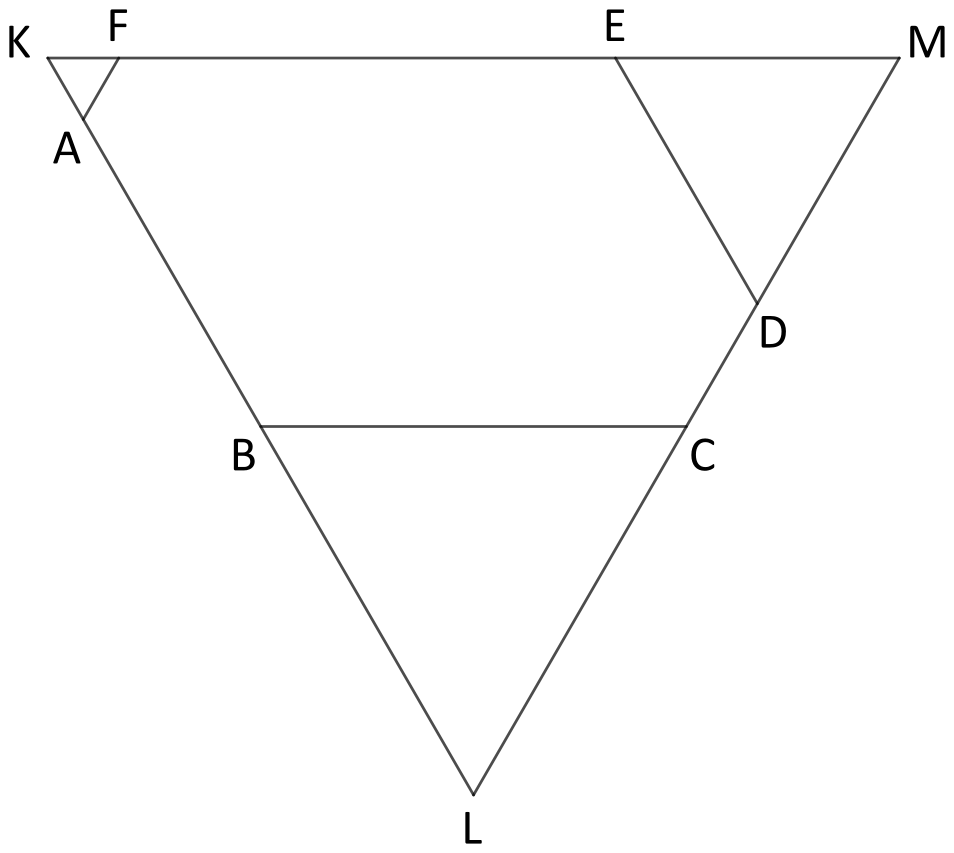
Možemo, stoga, preformulirati zadatak u matematički problem pridruživanja brojeva nekim $A$, $B$, $C$ i $D$ (ove oznake nemaju veze s originalnim točkama fizikalnog zadatka) i to tako da njihove razlike u parovima budu $7$, $8$, $10$, $15$, $18$ uz nepoznatu razliku. Primijetimo zanimljivo svojstvo: uzmemo neka tri slova $X$, $Y$ i $Z$ i definiramo uređaj, na primjer $X>Y>Z$. Tada je razlika $X-Z$ zbroj razlika $X-Y$ i $Y-Z$ (očito $(X-Y)+(Y-Z)=X-Z$). Dakle, ako uzmemo bilo koju trojku brojeva, jedna od razlika između njih bit će zbroj preostale dvije.

Vratimo se početnom zadatku. Recimo da je nepoznata razlika upravo razlika između $C$ i $D$. Uzmimo brojeve $A$, $B$ i $C$. Sve tri razlike među njima su poznate. Budući da jedna mora biti zbroj druge dvije imamo samo dvije mogućnosti: $7+8=15$ ili $8+10=18$. Slično vrijedi za $A$, $B$ i $D$, pa jedna od te dvije trojke mora imati razlike $7$, $8$ i $15$, a druga $8$, $10$ i $18$. Neka je trojka $A$, $B$ i $C$ (u nekom poretku) ona s razlikama $7$, $8$ i $15$. Trojke $A$, $B$, $C$ i $A$, $B$, $D$ se podudaraju samo u razlici između $A$ i $B$ pa upravo ta razlika mora biti $8$ (to je jedina vrijednost razlika koja se pojavljuje u obje trojke $7$, $8$, $15$ i $8$, $10$, $18$).

Za sada se brojevi $A$ i $B$ mogu međusobno zamijeniti, tako da možemo izabrati da razlika između $A$ i $C$ bude $15$, a da razlika između $B$ i $C$ bude $7$. U trojki $A$, $B$, $C$ brojevi $A$ i $C$ su ili najveći ili najmanji. Odaberimo ih tako da $A$ bude najveći. Imamo dvije mogućnosti za razliku između $D$ i brojeva $A$ i $B$.

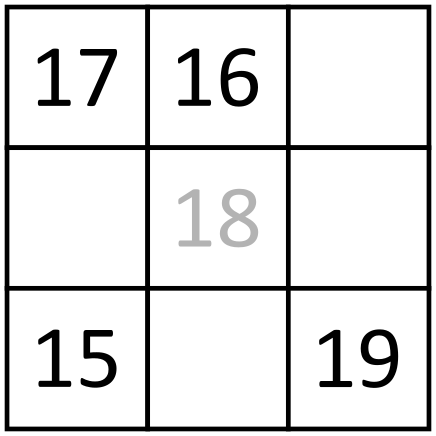
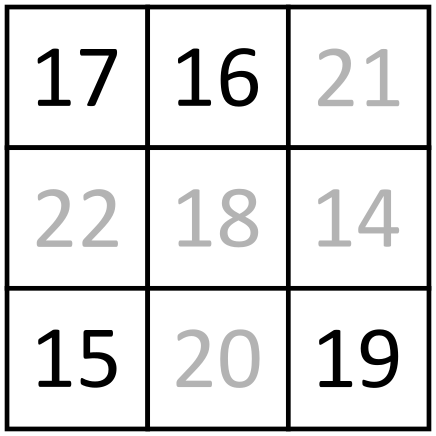
1. slučaj: razlika između $A$ i $D$ je $18$. To znači da je u trojki $A$, $B$, $D$ jedan od brojeva $A$ i $D$ je najveći, a drugi najmanji. Međutim, u trojki $A$, $B$, $C$ odabrali smo $A$ za najveći broj, dakle $A$ je veći od $B$ pa onda i najveći u trojki $A$, $B$, $D$. Sve ovo daje da je $A$ za $15$ veći od $C$ i za $18$ veći od $D$. Dakle, razlika između $C$ i $D$ je $(A-15)-(A-18)=3$. To je naše prvo rješenje.

2. slučaj: razlika između $A$ i $D$ je $10$. To znači da je u trojki $A$, $B$, $D$ jedan od brojeva $B$ i $D$ najveći, a drugi najmanji. Slično prvom slučaju znamo da je $A$ veći od $B$, pa je $B$ očito najmanji u trojki. Iz toga slijedi da je $C$ za $7$ manji od $B$ i da je $D$ za $18$ veći od $B$. To znači da je razlika između $C$ i $D$ $(B+18)-(B-7)=25$. To je drugo rješenje.

Konačno, vidimo da nepoznata razlika može biti samo $3$ ili $25$. U kontekstu početnog problema to znači da nepoznati napon može biti samo $3V$ ili $25V$. Zbroj mogućih nepoznatih napona je $3V+25V=28V$.

Rezultat:

$91$

Prije nego što počnemo, pogledajmo površinu jednakostraničnog trokuta sa stranicom duljine $x$. Pomoću Pitagorinog poučka lako je izračunati da je visina ovog trokuta $\frac{\sqrt{3}}{2}x$. Dakle, površina jednakostraničnog trokuta je $\frac{x\cdot \frac{\sqrt{3}}{2}x}{2}=\frac{\sqrt{3}}{4}{x}^2$.

Sada se vratimo na izvorni problem. Označimo vrhove šesterokuta $A$, $B$, $C$, $D$, $E$, $F$, tako da je $\mathit{AB}=10m$, $\mathit{BC}=12m$, $\mathit{CD}=4m$, $\mathit{DE}=8m$, $\mathit{EF}=14m$, $\mathit{FA}=2m$. Produljimo pravce $\mathit{AB}$, $\mathit{CD}$ i $\mathit{EF}$ kako bismo dobili trokut $\mathit{KLM}$ kao na slici:

Kako su unutarnji kutovi šesterokuta $\mathit{ABCDEF}$ $120^{\circ }$, dobivamo da su trokuti $\mathit{KAF}$, $\mathit{LBC}$ i $\mathit{MDE}$ jednakostranični. To odmah daje da je trokut $\mathit{KLM}$ jednakostraničan s duljinom stranice $24m$.

Površina šesterokuta $\mathit{ABCDEF}$ dana je kao razlika površine jednakostraničnog trokuta $\mathit{KLM}$ i zbroja površina jednakostraničnih trokuta $\mathit{KAB}$, $\mathit{LBC}$ i $\mathit{MDE}$. Dakle, površina šesterokuta $\mathit{ABCDEF}$ je:

To znači da je $a=91$.

Rezultat:

$75$

Neka $P_1$ označava površinu prvog klipa, $P_2$ površinu drugog klipa, a $P_3$ površinu trećeg klipa. Prema uvjetima zadatka, $P_1=P_2+P_3$.

Nadalje, neka je $m$ masa kunića i $\mathrm{\Delta }{h}_1=15\mathrm{mm}$ visina za koju se prvi klip pomakne prema dolje kad Maja na njega položi kunića. Istovremeno, drugi se klip pomakne prema gore za $\mathrm{\Delta }{h}_2$, a treći za $\mathrm{\Delta }{h}_3$. Nakon stavljanja kunića na prvi klip, događaju se dvije stvari. Najprije, dio vode ispod prvog klipa mora se podijeliti između drugog i trećeg klipa. To nam daje jednadžbu $P_1\mathrm{\Delta }{h}_1=P_2\mathrm{\Delta }{h}_2+P_3\mathrm{\Delta }{h}_3$. S druge strane, tlak sva tri klipa mora biti jednak. Ako s $p$ označimo početni tlak sustava, a s $\rho$ gustoću vode, dobivamo $p+\frac{\mathit{mg}}{P_1}-\mathrm{\Delta }{h}_1\mathit{\rho g}=p+\mathrm{\Delta }{h}_2\mathit{\rho g}=p+\mathrm{\Delta }{h}_3\mathit{\rho g}$. Oduzimanjem $p$ i dijeljenjem s $g$ slijedi $\frac{m}{P_1}-\mathrm{\Delta }{h}_1\rho =\mathrm{\Delta }{h}_2\rho =\mathrm{\Delta }{h}_3\rho$. Druga jednakost daje nam $\mathrm{\Delta }{h}_2=\mathrm{\Delta }{h}_3$. Uvrstimo li to u prethodne jednadžbe, dobivamo sljedeće:

Drugim riječima,

Usporedimo li te dvije jednadžbe, slijedi:

Neka sada $\mathrm{\Delta }{h}_2$ i $\mathrm{\Delta }{h}_3$ označavaju, redom, visine za koje se drugi i treći klip pomaknu prema dolje kad Maja na njih stavi kunića. Kao i prije, dolazimo do jednakosti:

Podijelimo li prve dvije jednakosti i iskoristimo da je $P_1=P_2+P_3$, dobivamo sljedeće:

Iz $P_1=P_2+P_3$ slijedi da je $P_3=P_1-P_2=P_1-\frac{2}{3}{P}_1=\frac{1}{3}{P}_1$. Dijeljenjem prve i treće jednakosti iz prethodnog skupa dobivamo:

Dakle, stavi li Maja kunića na treći klip, on se pomakne prema dolje $75\mathrm{mm}$.

Rezultat:

$999$

Matijin omiljeni broj ne može biti jednoznamenkast. Ako bi bio jednak znamenki $a$, uvjet nam daje $a^2=a$ što je istina samo za $a=0$ ili $a=1$, ali broj mora biti veći od $1$.

Matijin omiljeni broj ne može biti niti dvoznamenkast. Zaista, ako je broj $10a+b$ imali bismo ${(a+b)}^2=\mathit{ab}$ ili $a^2+\mathit{ab}+b^2=0$. Međutim, budući da su $a$ i $b$ nenegativni i $a$ je pozitivan, uvijek imamo $a^2+\mathit{ab}+b^2>0$, pa nikad ne može vrijediti $a^2+\mathit{ab}+b^2=0$.

Sada ćemo pokazati da je $999$ jedini troznamenkasti broj sa zadanim svojstvima. Lako se provjeri da $999$ zadovoljava zadana svojstva (${(9+9+9)}^2=27^2=3^6=9^3=9\cdot 9\cdot 9$).

Neka je $100a+10b+c$ broj sa zadanim svojstvima, znači da vrijedi ${(a+b+c)}^2=\mathit{abc}$. Brojevi $a$, $b$ i $c$ su znamenke, pa mora biti $0\le a,b,c\le 9$. Jasno, ako je neka od znamenki jednaka $0$, zbog relacije ${(a+b+c)}^2=\mathit{abc}$ moraju i sve preostale znamenke biti $0$, stoga možemo pretpostaviti $1\le a,b,c$. Nadalje, relacija ${(a+b+c)}^2=\mathit{abc}$ je simetrična u odnosu na vrijednosti $a$, $b$, $c$, pa možemo pretpostaviti $a\le b\le c$ (zbog ovog uvjeta ćemo dobiti najmanji troznamenkasti broj od bilo koje trojke koja zadovoljava uvjete). Dakle, pretpostavljamo

Promotrimo izraz ${(a+b+c)}^2=\mathit{abc}$. To se može zapisati kao $a^2+b^2+c^2+2\mathit{ab}+2\mathit{ac}+2\mathit{bc}=\mathit{abc}$. Iskoristimo li $c\le 9$, dobivamo $\mathit{abc}\le 9\mathit{ab}$. S druge strane, koristeći $a\le b\le c$ imamo:

Također, ${(a-b)}^2\ge 0$ pa je $a^2+b^2\ge 2\mathit{ab}$. Kombinirajući ove nejednakosti dobivamo:

Budući da su lijeva i desna strana ove nejednakosti jednake, moramo imati jednakosti u svim nejednakostima.

• U nejednakosti $\mathit{abc}\le 9\mathit{ab}$ vrijedi jednakost ako i samo ako je $c=9$.
• U nejednakosti $\mathit{ac}\ge \mathit{ab}$ vrijedi jednakost ako i samo ako je $b=c$.
• U nejednakosti $\mathit{bc}\ge \mathit{ab}$ vrijedi jednakost ako i samo ako je $a=c$.

Spajajući ova tri zapažanja dobivamo da je jedini mogući slučaj $a=b=c=9$. Kako smo već provjerili, to je zaista i rješenje. Dakle, broj $999$ je jedini troznamenkasti broj koji zadovoljava zadana svojstva. To je najmanji cijeli broj veći od $1$ sa traženim svojstvom, što znači da je $999$ Matijin omiljeni broj.

Rezultat:

$250$

Radimo slično kao u zadatku 25., samo što ovaj put moramo i razmisliti što različiti koeficijenti trenja rade. Usredotočimo se samo na smjer u kojem su koeficijenti trenja $f_1=0,1$ i $f_3=0,3$. Znamo da u formuli $F_f=\mathit{fF}$ ova sila predstavlja maksimalnu silu trenja, tj. $F_f\le \mathit{fF}$. Na ovaj način dobivamo dvije sile trenja $F_{f_1}\le f_{1}F$ i $F_{f_3}\le f_{3}F$. Kad bi ove dvije sile bile različite, uzrokovale bi moment sile (oko osi koja prolazi kroz druge dvije robotove ruke) na robotu. Mora, dakle, vrijediti $F_{f_1}=F_{f_3}$. Kombiniranjem dvije nejednakosti uz $f_1\le f_3$, dobivamo $F_{f_1}=F_{f_3}=f_{1}F$. Slično za $f_2=0,2$ i $f_4=0,4$ imamo $F_{f_2}=F_{f_4}=f_{2}F$. Kako bismo kompenzirali gravitacijsku silu $F_g=\mathit{mg}$ treba nam: