Zadania

Wynik:

W roku 2012 wysokość jabłoni wynosiła . Przez następne 10 lat, jabłoń rosła o dodatkowe rocznie. Tak więc jej wysokość w roku 2022 wynosi .

Wynik:

Wystarczy policzyć boki kwadratów, wzdłuż których szła Ania. Łatwo doliczyć się boków, co odpowiada odległości .

Wynik:

Średnia prędkość Grzesia jest równa wynikowi dzielenia całkowitej przebytej przez niego drogi przez czas, który zajęło mu przebycie tej drogi. Z wykresu możemy odczytać, że Grześ pokonał dystans w ciągu , co oznacza, że jego średnia prędkość wyniosła .

Wynik:

Najpierw musimy zebrać literę N. Gdybyśmy wybrali literę N o dwa pola na prawo od punktu startowego, musielibyśmy następnie wziąć literę Á o jedno pole na prawo i w dół od tego N. Jednak stamtąd nie da się dojść do żadnej litery B za pomocą dozwolonych ruchów. To znaczy że że musimy użyć litery N która jest poniżej punktu startowego.

Jeśli teraz wzięlibyśmy Á na trzy pola na prawo od tego N, mielibyśmy ten sam problem co poprzednio - nie znajdziemy żadnego B. Tak więc drugą spotkaną literą musi być Á w pierwszej kolumnie.

Jeśli za następną literę wybierzemy B w lewym dolnym rogu, będziemy mieli już tylko jeden sposób żeby dojść do pola z literą J. Po drodze miniemy również literę O, więc jest to jedna z poprawnych możliwości.

Jeśli będziemy zaś kontynuowali z literą B w trzecim wierszu, wówczas na dwa sposoby możemy dojść do litery O. Jeśli wybierzemy O w najniższym wierszu, będziemy mieli już tylko jeden sposób aby dojść do prawego dolnego rogu. Natomiast jeśli weźmiemy O z trzeciego wiersza, będziemy mieli trzy różne sposoby przejścia do J.

Wszystkie możliwe trasy pionka są przedstawione na rysunku:

Daniel może przeprowadzić pionek na różnych sposobów.

Wynik:

Będziemy nazywać kierunki zgodnie z rysunkiem. Wiązka odbiła się od prawej ściany tak, że oświetli lewą ścianę dodatkowy metr wyżej. To oznacza, że trafi w punkt na lewej ścianie położony dwa metry wyżej niż miejsce, z którego została wypuszczona. Odbije się potem tak, że oświetli punkt na prawej ścianie położony dodatkowy metr wyżej, więc uderzy dokładnie w róg, w którym znajduje się balonik. Tor wiązki jest widoczny na rysunku poniżej:

Wiązka odbije się od ścian razy.

Wynik:

Laura może przebyć na swoim rowerze kilometry w jedną godzinę. Skoro kilometry to doszkół, Laura może przebyć doszkołów w ciągu jednej godziny. Jednak jedna szkolekcja to tylko godziny. Jeśli Laura pokona doszkołów w godzinę, to w trzy czwarte godziny (czyli jedną szkolekcję) pokona doszkołów. Stąd Laura może jeździć na rowerze z prędkością doszkołów na godzinę.

Wynik:

Rozważmy wszystkie możliwe wartości pierwszej cyfry. Jedyna liczba rozpoczynająca się od zera to . Nie jest ona jednak dodatnia, więc Ola ją pomija. Jeśli pierwszą cyfrą jest , możemy albo dopisać po jej prawej stronie zero, albo nie dopisywać nic. To daje nam rozwiązania i . Jeśli pierwszą cyfrą jest , możemy po jej prawej stronie dopisać jeden i/lub zero. To daje nam rozwiązania , , , . Zatem istnieje liczb zstępujących.

Wynik:

Mateusz przebiegł z prędkością . To oznacza, że przebiegł trasę w .

Marek jechał z prędkością , więc pokonanie trasy zajęło mu . Ponieważ dał Mateuszowi minut zapasu, skończył po starcie Mateusza.

Tak więc Marek skończył wyścig wcześniej.

Wynik:

Czy numery zarezerwowanych siedzeń mogły zawierać którąkolwiek z cyfr , , , , lub ? Gdyby tak było, albo początkowo albo po zamianie cyfr miejscami liczba byłaby podzielna przez lub . Dlatego numer żadnego z zarezerwowanych siedzeń nie zawiera tych cyfr. Numery te będą składały się tylko z cyfr , , lub . Jest tylko liczb spełniających ten warunek:

Spośród tych liczb, złożone są: , , , , oraz , te liczby musimy więc odrzucić. Musimy także odrzucić , ponieważ po zamianie jej cyfr dostajemy liczbę złożoną. Pozostają nam liczby:

Mateusz mógł więc kupić co najwyżej biletów.

Wynik:

Długość zjeżdżalni możemy obliczyć z twierdzenia Pitagorasa. Wynosi ona . Wiemy, że zjechanie ze ślizgawki zajmuje . Zatem zjeżdżające dziecko ma średnią prędkość .

Wynik:

Prostokąt można podzielić na dwa mniejsze prostokąty tylko przez użycie odcinka równoległego do jednego z boków tego prostokąta. W takim wypadku odcinek ten będzie miał taką samą długość jak bok, do którego jest równoległy.

Z treści zadania wiemy, że ogród to prostokąt o obwodzie , którego jeden z boków ma długość . Drugi z boków ma zatem długość taką, że zachodzi . Z tego otrzymujemy .

Z obserwacji z początku rozwiązania wynika, że bok o długości musi mieć taką samą długość jak druga ścieżka dzieląca ogród na dwa przystające prostokąty. Zatem ścieżka ta ma długość .

Wynik:

Zastosujemy zasadę akcji i reakcji. Mówi ona, że jeśli jakiś obiekt działa na inny obiekt z pewną siłą , to obiekt działa na obiekt z siłą o równej wartości i kierunku, ale przeciwnym zwrocie. W naszym zadaniu Ziemia przyciąga Mateusza siłą grawitacyjną o wartości . Mateusz musi więc działać na Ziemię równie dużą siłą grawitacyjną, a więc siłą o wartości .

Wynik:

Oznaczmy przez dystans, który pokonała Sabina. Gdyby nie zatrzymywała się w trakcie trasy, pokonanie tego dystansu zajęłoby jej . Ze względu na to, że zrobiła sobie 30 minut przerwy, przebyła całą trasę w czasie . Właśnie z powodu tego postoju, średnia prędkość Sabiny na całej trasie wyniosła tylko . Prowadzi to do równania: Zatem Sabina pokonała dystans .

Wynik:

O musiał się pomylić ktoś, kto typował największą lub najmniejszą liczbę. Gdyby była to osoba zgadująca najmniejszą liczbę, to liczba rozwiązanych zadań musiałaby wynosić albo . Pierwsza opcja jest niepoprawna, bo w takim przypadku wszyscy inni myliliby się przynajmniej o . Druga opcja również jest niepoprawna, bo pozostałe osoby musiałyby mylić się o , i , co nie zgadza się z wartościami podanymi w treści zadania.

Zatem to osoba typująca musiała być tą, która pomyliła się o . Z analogicznego powodu jak w poprzednim przypadku, liczba rozwiązanych zadań nie może wynosić , wynosi więc . W tym przypadku pozostałe typy różnią się o , i , co odpowiada wartościom podanym w treści zadania.

Zatem drużyna poprawnie rozwiązała zadań.

Wynik:

Pomyślmy, co wynika z tego, gdy ktoś powie, że ktoś inny (nie) jest szpiegiem. Przykładowo, Ala twierdzi, że Dominik jest szpiegiem. Jeśli Ala mówi prawdę (czyli nie jest szpiegiem), Dominik jest szpiegiem. Jeśli Alia kłamie (czyli jest szpiegiem), Dominik nie jest szpiegiem. Oznacza to, że Ala i Dominik mają różne role – jedno z nich jest szpiegiem, a drugie nie. Teraz popatrzmy na stwierdzenie Bartka. Jeśli mówi prawdę (czyli nie jest szpiegiem) to Celina również nie jest szpiegiem. Jeśli jednak Bartek kłamie (czyli jest szpiegiem) to Celina też jest szpiegiem. Stąd Bartek i Celina muszą być po tej samej stronie – albo obydwoje są szpiegami, albo żadne z nich nie jest. Ponadto Dominik i Edek również mają tą samą rolę. Jeśli Ala byłaby szpiegiem, to jedna z par – Bartek i Celina lub Dominik i Edek także musiałaby być parą szpiegów. Wtedy mielibyśmy co najmniej troje szpiegów, co jest niemożliwe. Stąd Ala nie może być szpiegiem, a skoro twierdzi ona, że Dominik jest szpiegiem, to musi on nim być. Wiemy, że Dominik jest po stronie Edka, więc Edek również musi być szpiegiem.

Szpiegami są zatem Dominik i Edek, a suma ich numerów wynosi .

Wynik:

Oznaczmy przez rozmiar pliku. Jeśli Marian prześle plik bez kompresji, zajmie mu to czas . Jeśli Marian postanowi skompresować plik, sama kompresja zajmie czas . Po kompresji, rozmiar pliku będzie wynosił . Po sekundach Marian zacznie przesyłać plik i sam przesył zajmie czas . W takim razie cały proces z kompresją zajmie czas . Treść zadania mówi, że ten czas jest równy czasowi przesyłu pliku bez kompresji. To prowadzi do równania, które jesteśmy w stanie rozwiązać: W takim razie rozmiar pliku wynosi .

Wynik:

Zauważmy, że obwód ogródka jest równy sumie obwodów grządek o obwodach , i grządki zaznaczonej znakiem zapytania. Jest tak dlatego, że możemy przenieść długości niektórych boków tych trzech grządek, żeby w sumie stworzyły całą granicę ogródka:

Stąd wnioskujemy, że obwód grządki oznaczonej znakiem zapytania wynosi .

Wynik:

Im wcześniej Adrian zacznie hamować, tym mniej siły hamowania będzie potrzebował. Załóżmy, że auto zaczyna hamować w odległości . Aby zatrzymać samochód, auto musi wykonać pracę w celu przezwyciężenia siły hamowania kosztem swojej energii, w tym przypadku energii kinetycznej.

Energia kinetyczna auta o masie oraz prędkości wynosi . Praca o tej samej wielkości musi zostać wykonana przez siłę o wielkości , którą auto przezwycięża siłę hamowania o tej samej wielkości. Ta siła wykonuje na dystansie pracę . To prowadzi do równania: W takim razie, siła hamowania działająca na auto musi mieć wielkość co najmniej:

Wynik:

Nie da się za pomocą dostępnych nominałów uzbierać kwoty . Musielibyśmy w tym celu użyć lub monety o wartości . W obu przypadkach, nie da się pozostałej kwoty zapłacić tylko za pomocą monet o wartości . Jesteśmy jednak w stanie zapłacić dowolną kwotę większą niż . Zacznijmy od kwoty (), () oraz (). Skoro jesteśmy w stanie zapłacić te trzy kwoty, możemy też uzbierać dowolną większą kwotę, potrzebujemy tylko wystarczająco dużo monet o nominale .

W takim razie największa możliwa wartość zakupów Magdy wynosi .

Wynik:

Cała konfiguracja jest symetyczna względem osi znajdującej się pomiędzy kulami. Pozostanie ona symetryczna nawet po zderzeniu, gdy kule stworzą większą masę. Gdyby masa po zderzeniu zaczęła poruszać się w lewo lub w prawo, konfiguracja przestałaby być symetryczna. Możemy więc wywnioskować, że masa powstała po zderzeniu kul nie będzie się już poruszała.

Po zderzeniu kule tracą całą swoją energię kinetyczną, która zgodnie z założeniem zadania przekształca się w ciepło. To ciepło przepływa do powstałej masy, ogrzewając ją. Każda z kul (o masie i szybkości ) ma energię kinetyczną . Ich łączna energia kinetyczna wynosi zatem . Ta energia jest dostarczana modelinowej masie w formie ciepła. Ma ona masę (bo składa się z dwóch kul o masie ), ciepło właściwe , a jej temperatura zmieni się o . Stąd mamy: Jeśli temperatura kul przed zderzeniem wynosiła , to temperatura masy po zderzeniu wyniesie:

Wynik:

Aby zrównoważyć huśtawkę, momenty sił działające na obie jej strony muszą być równe. Daniel ma masę i siedzi w odległości od punktu obrotu huśtawki. Na Daniela działa siła ciężkości . Daniel działa na huśtawkę siłą o tej samej wartości, co daje moment siły: Sześciany po drugiej stronie huśtawki muszą łącznie działać z momentem siły o tej samej wartości. Załóżmy, że jest sześcianów. W treści podano, że każdy sześcian ma masę oraz bok długości . Ich środek ciężkości jest w odległości od punktu obrotu huśtawki. Jest to punkt, w którym siła ciężkości działa na huśtawkę. Moment siły działający na huśtawkę z drugiej strony wynosi więc: Momenty sił i muszą być równe. Dostajemy: Więc liczba sześcianów położonych przez Ninę to:

Wynik:

Rozważmy cyfry, które mogą stanowić cyfry jedności. Cyfry , i nie mogą znajdować się na końcu, bo wtedy powstałe liczby byłyby podzielne przez 2, a więc nie byłyby pierwsze. Podobnie, 5 też nie może być ostatnią cyfrą, bo wtedy tworzona przez nią liczba byłaby podzielna przez . Stąd wnioskujemy, że cyfry , , i będą cyframi dziesiątek, a pozostałe cyfy (, , i ) będą cyframi jedności. Stąd jedyna możliwa, a więc i maksymalna suma utworzonych liczb pierwszych musi być równa .

Uwaga: Przy użyciu tych kart naprawdę da się stworzyć cztery liczby pierwsze, na przykład: , , i .

Wynik:

Dwie proste na płaszczyźnie, które się nie przecinają, są równoległe. Szukamy więc liczby par prostych równoległych, przechodzących przez wierzchołki siedmiokąta foremnego.

Oznaczmy zaznaczone punkty jako , , , , , i . Znajdźmy teraz wszystkie proste równoległe do , przechodzące przez pewne dwa wyznaczone punkty. Są to proste wyznaczane przez i . Wynika to z faktu, że siedmiokąt foremny jest symetryczny względem symetralnej odcinka . Z tej symetrii wynika, że proste , i są prostopadłe do symetralnej odcinka , a więc są parami równoległe. W ten sposób znajdujemy pary prostych równoległych.

Powtarzając to samo rozumowanie dla , , , , i dostajemy w każdym przypadku po kolejne pary prostych równoległych.

Każda prosta przechodząca przez któreś dwa z punktów od do jest równoległa do dokładnie jednego z odcinków , , , , , i (odcinki te są do siebie parami nierównoległe). Zatem rozpatrzyliśmy wszystkie możliwe przypadki.

Teresa może narysować dwie proste równoległe na sposobów.

Wynik:

Energia potencjalna piłki w chwili podrzucenia wyniosła , gdzie to masa piłeczki, to wysokość, z jakiej Iga ją wyrzuciła, a to przyspieszenie ziemskie. Jeśli oznaczymy , to energia kinetyczna piłki w chwili rzucania wyniosła . Całkowita energia piłki była zachowana przez cały czas trwania ruchu, więc wartość była w każdej chwili stała, również zaraz przed tym, gdy piłka uderzyła w ziemię. W tej chwili piłka znajdowałą się na wysokości zero, więc miała zerową energię potencjalną. Stąd cała jej energia musiała być równa jej energii kinetycznej. Jeśli oznaczymy tą energię kinetyczną przez , otrzymamy równanie:

Stąd prędkość piłki tuż przed wylądowaniem to:

Wynik:

Jedyną liczbą jednocyfrową, która jest równa -krotności sumy swoich cyfr, jest . Niezależnie od tego, czy potraktujemy jako liczbę naturalną (a jest to kwestia kontrowersyjna w różnych dziedzinach matematyki), czy nie, nie wpłynie to na sumę liczb znalezionych przez Jonasza.

Jeśli Jonasz znalazłby dwucyfrową liczbę o zadanej własności, moglibyśmy zapisać ją w formie , gdzie i to jej cyfry. Jednak -krotność sumy jej cyfr wyniosłaby , a zachodzi . To prowadzi do wniosku, że Jonasz nie mógł znaleźć żadnej liczby dwucyfrowej.

Dalej rozważmy liczby trzycyfrowe. Każda z nich może zostać zapisana jako gdzie . Warunek dotyczący sumy cyfr prowadzi do zależności: Jeśli , to otrzymujemy trzy możliwe wartości cyfr i . Tymi możliwymi wartościami par są , oraz , co odpowiada liczbom , i . Okazuje się, że nie mamy innych możliwości na wartość cyfry , ponieważ oraz dla otrzymalibyśmy , co przeczyłoby równaniu, gdyż . W takim razie nie znajdziemy więcej opcji dla liczb trzycyfrowych.

Liczba czterocyfrowa ma sumę cyfr równą co najwyżej , więc trzynastokrotność sumy jej cyfr na pewno będzie mniejsza niż (oczywiście moglibyśmy także policzyć ile wynosi , ale nawet takie luźne szacowanie wystarcza nam do wysnucia potrzebnego wniosku). W takim razie, można powiedzieć, że -krotność sumy cyfr na pewno nie będzie liczbą czterocyfrową. Z tego wnioskujemy, że Jonasz nie mógł znaleźć żadnej czterocyfrowej liczby. Ten sam argument można zaaplikować dla liczb o większej liczbie cyfr.

Podsumowując, suma liczb znalezionych przez Jonasza wyniosła .

Wynik:

Obydwie przekątne kwadratu mają tę samą długość i są do siebie prostopadłe. Wiemy, że długość przekątnej znaku wynosi . Każda z przekątnych dzieli kwadrat na dwa trójkąty, których wysokością jest połowa drugiej przekątnej. Taki trójkąt ma pole . Cały znak składa się z dwóch takich trójkątów, więc ma pole = 72 dm².

Żółta część stanowi całego znaku, więc jej pole wynosi . Stąd bok kwadratu ma długość .

Wynik:

Niech oznacza długość ruchomego chodnika. Możemy wyznaczyć prędkość chodnika ruchomego. Przejechanie z z jednego końca chodnika na drugi zajęło Beacie , czyli prędkość taśmy chodnika wynosi . Podobnie możemy wyznaczyć prędkość chodzenia Beaty. Skoro przejście tej trasy zajęło Beacie , jej prędkość wynosi .

Kiedy Beata idzie po chodniku w kierunku przeciwnym do jego ruchu, porusza się z prędkością . Tak więc dojście na drugi koniec chodnika zajmie: Gdy natomiast Beata idzie zgodnie z kierunkiem ruchu chodnika, porusza się z prędkością . Tym razem przejście całego chodnika zajmie: Zatem odpowiedź wynosi:

Wynik:

Najpierw spróbujmy zrozumieć, jak wyglądają zbiory i . Wyrażenie , zwane także wartością bezwględną, jest tak naprawdę równe odległości liczby od na osi liczbowej. Może nie jest to natychmiastowo widoczne z definicji tego wyrażenia z treści zadania, ale wartość bezwględna po prostu usuwa znak liczby . Rozważmy wyrażenie . Jeśli oraz , to . Zależność jest wtedy równoważna , czyli . Widzimy więc, że punkty spełniające tę zależność tworzą prostą przechodzącą przez punkty oraz . Musimy jednak pamiętać, że założyliśmy warunek oraz , dlatego musimy przyciąć tę prostą tak, by pozostawić jedynie jej fragment znajdujący się w pierwszej ćwiartce układu współrzędnych. W ten sposób dostajemy odcinek łączący punkty i na płaszczyźnie. Jeżeli rozważymy pozostałe przypadki znaków i (łącznie jest ich 4), dostaniemy sumarycznie, że zbiór A składa się z odcinków łączących i , i , i oraz i . Odcinki te tworzą na płaszczyźnie kwadrat o wierzchołkach w punktach , , oraz .

Teraz przeanalizujmy zbiór B. Opisuje go relacja . Ta funkcja, zwana maksimum, zwraca liczbę większą spośród oraz . Aby funkcja ta zwróciła , co najmniej jedna z liczb i musi być równa , zaś druga musi być niewiększa niż . Jeśli , to lub . W tym przypadku musi zachodzić , czyli . Dla , warunek ten jest spełniony dla punktów na odcinku łączącym punkty oraz , zaś dla , warunek zachodzi dla punktów na odcinku łączącym punkty oraz . Możemy powtórzyć to rozumowanie dla . To dodaje nam do zbioru odcinki łączące punkty z ) oraz z . W takim razie, zbiór także jest kwadratem, ale tym razem o wierzchołkach , , oraz .

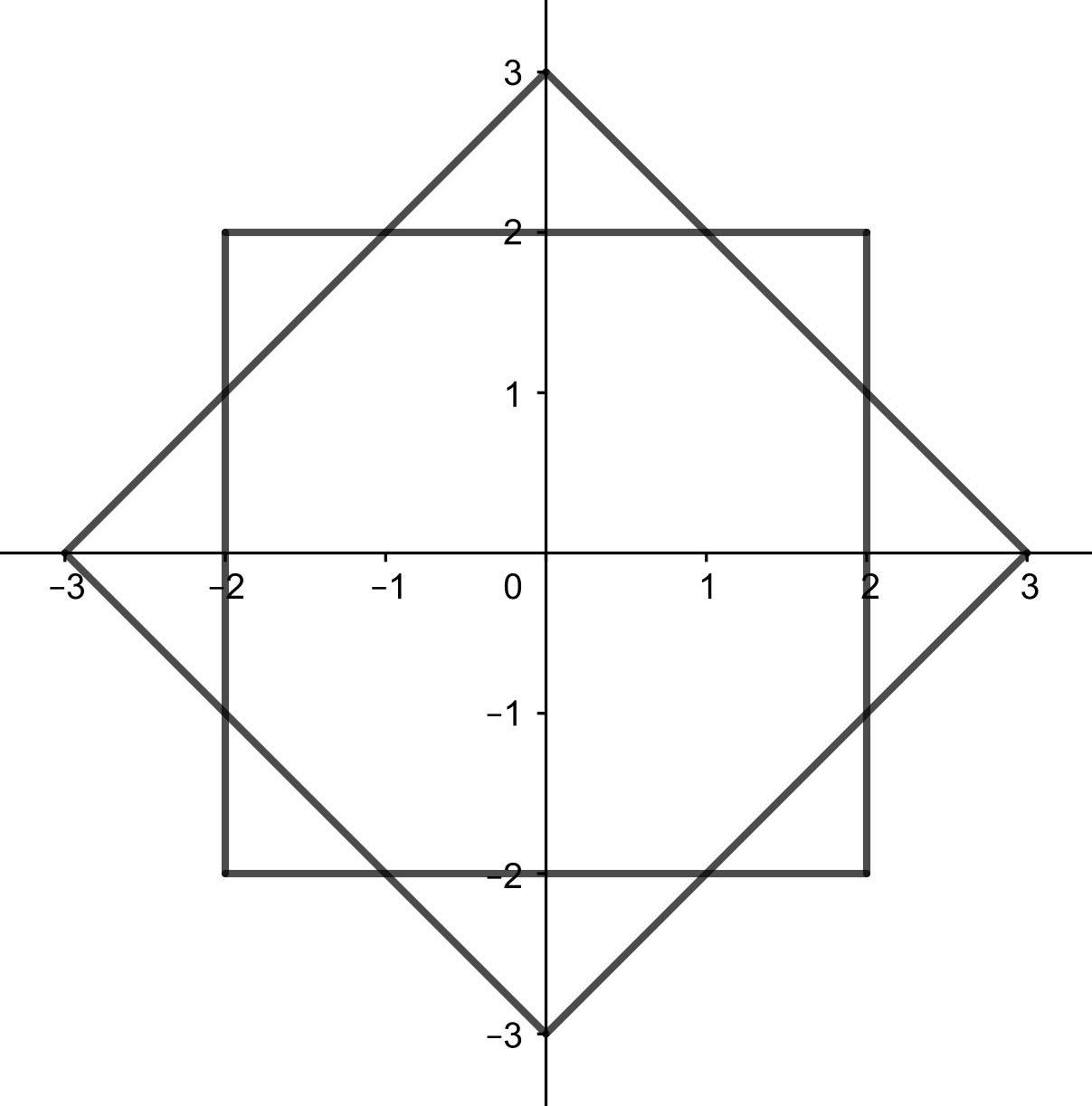
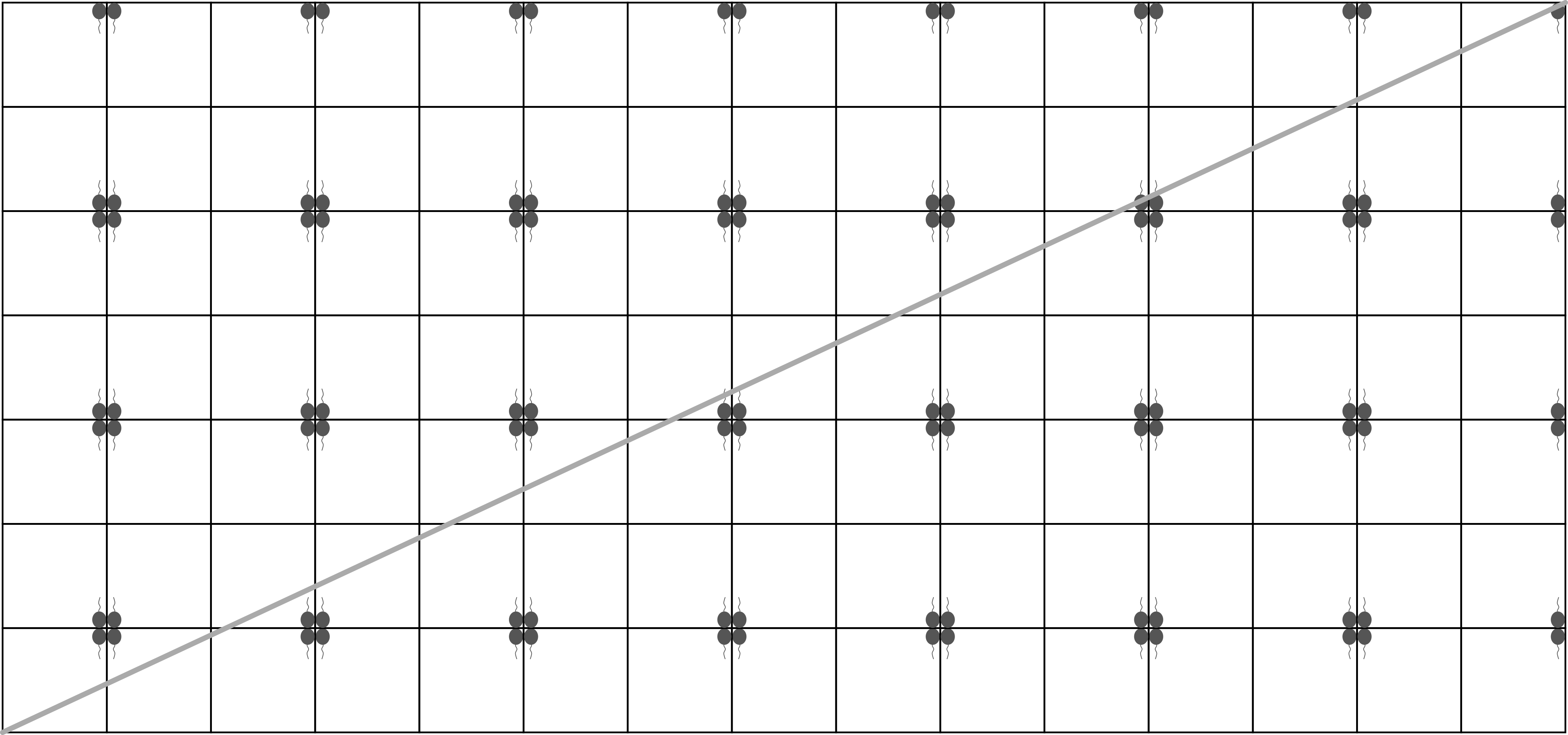
Zbiory oraz zostały przedstawione na rysunku:

Z rysunku łatwo odczytać, że kwadraty odpowiadające zbiorom i przecinają się w dokładnie punktach płaszczyzny. W takim razie liczba punktów należąca do obu zbiorów jednocześnie jest równa .

Wynik:

Załóżmy, że na prawej gałęzi znajduje się oporników, zaś na lewej jest ich . Musimy policzyć . Łączny opór oporników na prawej gałęzi jest równy , gdzie to opór jednego opornika. Oporniki na lewej gałęzi mają łączny opór . Wtedy opór całego obwodu jest równy: Treść zadania mówi, że opór całego obwodu jest -krotnie mniejszy niż opór oporników na prawej gałęzi. To daje nam równanie, z którego możemy wyliczyć : W takim razie na prawej gałęzi jest razy więcej oporników niż na lewej gałęzi.

Wynik:

Marianna wykona pracę w celu podniesienia kamienia o masie na taką wysokość, by cały kamień znalazł się ponad murkiem. W takim razie, musimy obliczyć, jaka jest najmniejsza wysokość na jaką musimy podnieść środek masy kamienia.

Środek ciężkości trójkąta dzieli każdą jego środkową w stosuku , przy czym dłuższa część znajduje się bliżej wierzchołka, z którego jest poprowadzona. W trójkącie równobocznym, każda środkowa jest także jego wysokością, co oznacza, że środkowa ma długość . Odległość środka ciężkości trójkąta od dowolnego jego boku jest wtedy równa . To oznacza, że środek ciężkości trójkąta znajduje się w odległości co najmniej od dowolnego punktu na boku trójkąta.

W pierwszym momencie, w którym kamień znajdzie się w całości ponad murkiem, będzie istniał punkt należący do trójkąta będącego podstawą kamienia, który będzie znajdował się na wysokości równej dokładnie wysokości murku (w innym wypadku moglibyśmy obniżyć lekko kamień i Marianna wykonałaby mniej pracy). Punkt ten jest odległy o co najmniej od środka ciężkości podstawy. Oznacza to, że musimy podnieść środek ciężkości podstawy (więc także środek masy kamienia) na wysokość co najmniej powyżej murku. Z drugiej strony, taka wysokość wystarczy nam do postawienia kamienia na murku: należy podnosić kamień tak, by jedna z jego podłużnych ścian była cały czas równoległa do powierzchni na szczycie murku.

Oznacza to, że Marianna musi podnieść kamień na wysokość , by zrównać wysokość środka masy ze szczytem murku, a następnie zwiększyć jego wysokość o dodatkowe by cały kamień znalazł się ponad murkiem. Sumarycznie należy podnieść środek masy o , co oznacza, że zwiększymy energię potencjalną kamienia o . Marianna wykona pracę równą dokładnie przyrostowi energii potencjalnej kamienia, czyli . W takim razie Marianna wykona pracę równą .

Wynik:

Załóżmy, że liczby zapisane przez Andrzeja to i oraz (w innym wypadku możemy po prostu zamienić liczby nazwami). Wtedy dwie dopisane przez niego liczby to oraz . Rozważmy przypadek, kiedy . Wtedy liczby na tablicy to , , , . Nieważne w jakiej kolejności ustawimy te liczby, znajdziemy dwa sąsiednie wyrazy równe oraz . W takim razie jeśli ciąg ten miałby być arytmetyczny, to jego różnica musi być równa . Znajdziemy także zawsze dwa sąsiednie wyrazy i , a skoro różnica jest równa , to . Taki przypadek nie może zajść, bo wiemy, że jest różne od .

Możemy więc założyć, że zapisane liczby są różne od , czyli . Wtedy, z całą pewnością, największą liczbą zapisaną na tablicy będzie , a drugą największą będzie . Ponieważ liczby w ciągu arytmetycznym muszą stale rosnąć lub stale maleć, liczby oraz muszą być dwoma sąsiadującymi wyrazami ciągu. W takim razie, dowolne dwa sąsiednie wyrazy muszą różnić się o , czyli . W takim razie, trzecią liczbą w ciągu musi być , czyli liczba o mniejsza od . Ostatnia liczba to , która musi być mniejsza o od . To daje nam warunek: Jeśli Andrzej wybierze liczby oraz na początku, po zapisaniu ich sumy i różnicy, otrzyma ciąg arytmetyczny , , , . Ostatnia rzecz, jaką musimy obliczyć, to ile par liczb oraz to jednocyfrowe liczby. Łatwo sprawdzić, że para musi być równa , lub . W takim razie Andrzej miał trzy sposoby na wybranie początkowych liczb.

Wynik:

Po pociągnięciu za sznurek, ruchome krążki będą poruszać się wraz z odważnikiem w górę. W trakcie tego procesu część liny przewiniętej przez krążki zniknie, bo będziemy przeciągać ją rękami. Obrazek pokazuje, co dzieje się gdy krążki unoszą się od dolnej przerywanej linii do górnej przerywanej linii – równe części sznurka znikają na pięciu odcinkach znajdujących się pomiędzy tymi liniami. Jeśli udało się nam przeciągnąć fragment sznurka o pewnej długości, odważnik i krążki unoszą się w taki sposób, że spomiędzy wspomnianych linii znikają fragmenty sznurka o łącznej długości równej tej części sznurka, którą przeciągneliśmy. Stąd odważnik porusza się w górę o jedną piątą długości fragmentu sznurka, który przeciągneliśmy. Jeśli ciągniemy za sznurek ze stałą prędkością , to odważnik jest podnoszony z prędkością .

Wynik:

Przypomnijmy, w jaki sposób obliczyć najmniejszą wspólną wielokrotność i największy wspólny dzielnik dwóch liczb. Najpierw musimy znaleźć rozkład każej z nich na czynniki pierwsze. Następnie, każdę liczbę pierwszą podnosimy do większej z potęg, w których ta liczba pierwsza występuje w rozkładach na czynniki pierwsze dwóch rozważanych liczb. Iloczyn tych potęg to najmniejsza wspólna wielokrotność naszych dwóch liczb. Podobnie obliczamy największy wspólny dzielnik, tylko tym razem każdą liczbę pierwszą podnosimy do mniejszej z odpowiednich potęg. Wynika stąd dobrze znana tożsamość . Niech teraz i będą dwoma liczbami spełniającymi warunki Tomasza. Mamy dla nich równości oraz . Łącząc je z wcześniej uzyskanymi równościami mamy: W związku z tym obie liczby i są wielokrotnościami , więc można je zapisać w postaci i dla pewnych liczb całkowitych dodatnich . Żeby znaleźć największą możliwą wartość musimy znaleźć największą możliwą wartość . Ponieważ największy wspólny dzielnik liczb i wynosi , to największy wspólny dzielnik liczb i musi wynosić . Ponadto wiemy, że: Suma dwóch liczb o zadanym iloczynie jest największa wtedy, kiedy ich różnica jest największa możliwa. Tak dzieje się, gdy oraz (lub na odwrót). W tym przypadku mamy i te dwie liczby mają największą możliwą sumę . Wracając do liczb i , znajdujemy że suma liczb Tomasza wynosi .

Wynik:

Popatrzmy na rozkład sił w tym układzie. Na środek ciężkości mostu o masie działa siła grawitacji, której wartość wynosi . Ponadto, każdy z łańcuchów działa pewną siłą na most. Skoro most się nie porusza, to również się nie obraca. Ten warunek jest równoważny temu, że suma momentów obrotowych działających na most wynosi zero. Siła grawitacji działająca na most w odległości od zawiasu przekłada się na moment obrotowy . Pionowa składowa siły łańcuchów działa w odległości i musi powodować moment siły . Stąd wiemy, że wartość tej składowej musi wynosić . Mamy dwa identyczne łańcuchy, więc pionowa składowa siły, z którą każdy z nich działa na most musi wynosić .

Znamy już pionową składową siły działającej na łańcuchy, ale jak znaleźć wartość tej siły działającej wzdłuż łańcucha? Zauważmy, że trójkąt, którego boki są wyznaczone przez ścianę, most i łańcuch jest podobny do trójkąta wyznaczonego przez siły , i odcinka łączącego ich końce. Stąd stosunek wartości sił i wynosi tyle ile stosunek wysokości bramy do długości łańcucha. Długość łańcucha możemy łatwo policzyć z twierdzenia Pitagorasa: . Mamy zatem:

Zatem na każdy z łańcuchów działa siła:

Wynik:

Policzmy na poczatku prawdopodobieństwo, że liczba wystąpień cyfry w pliku jest liczbą parzystą. Niech pierwsze cyfr będzie dowolnych. W związku z tym liczba wystąpień jedynek wśród tych cyfr może być parzysta lub nieparzysta. Ostatnia cyfra to lub . W zależności od ostatniej cyfry, parzystość liczby jedynek w pierwszych cyfrach zmienia się przez dodanie ostatniej cyfry lub nie. To, czy się zmieni, czy nie, jest równie prawdopodobne, ponieważ zależy wyłącznie od ostatniej cyfry, która zmienia parzystość z prawdopodobieństwem oraz zachowuje parzystość z prawdopodobieństwem .

Rozważmy teraz tylko takie zestawy cyfr, które mają parzystą liczbę wystąpień cyfry . Ile z nich ma liczbę wystąpień cyfry podzielną przez cztery? Jeśli liczba wystąpień cyfry jest parzysta, są dwa przypadki – albo jest ona podzielna przez cztery, albo reszta z dzielenia liczby wsytąpień cyfry wynosi . Rozważmy dwa zbiory, i . W zbiorze umieścimy wszystkie sytuacje, w których liczba jedynek jest podzielna przez cztery, a w zbiorze wszystkie sytuacje, w których ta reszta wynosi . Zauważmy, że możemy wybrać dowolną sytuację ze zbioru i zamienić wszystkie na , a na . Jeśli liczba jednyek w pierwotnym przypadku wynosiła , a liczba zer wynosiła , to po zamianie liczba jedynek będzie wynosić , a liczba zer będzie wynoscić . Reszta z dzielenia przez cztery to . Dlatego, po zamianie, sytuacja ze zbioru będzie należeć do zbioru . Zamieniając cyfry ponownie, otrzymamy sytuację z początkowego zbioru . W ten sposób możemy podzielić wszytkie możliwe sytuacje na pary, zawierające po jednej sytuacji ze zbioru i jednej ze zbioru . Każda sytuacja musi należeć do jednej z grup, a zatem zbiory i muszą zawierać tyle samo sytuacji.

Podsumowując, w sytuacjach, które mają parzystą liczbę jedynek, wystąpienie sytuacji z podzielną przez cztery liczbą jedynek ma prawdopodobieństwo . Stąd prawdopodobieństwo, że liczba wystąpień cyfry w pliku jest podzielna przez cztery wynosi .

Wynik:

Gdy spróbujemy narysować kilka pierwszych odbić, przekonamy się, że wiązka odbije się stosunkowo dużo razy, zanim trafi w balonik. Za każdym razem musielibyśmy również liczyć, w którym dokładnie miejscu laser odbija się od ściany, co nie jest proste. Zastosujmy zatem inne podejście.

Zamiast przerzucać wiązkę względem lini prostopadłej do ściany w punkcie odbicia, przerzucimy cały pokój względem ściany, od której odbił się laser. Załóżmy zatem, że po drugiej stronie prawej ściany naszego pokoju jest drugi pokój będący jego lustrzanym odbiciem, Jeśli pozwolilibyśmy promieniowi przechodzić przez ściany pomieszczenia, w lustrzanej wersji naszego pokoju miałby on taki sam przebieg, jak w wyjściowym pokoju, gdyby odbił się od ściany. Powtarzając ten proces wielokrotnie, odbijając pokoje względem ścian, w które uderzył promień lasera, uzyskujemy wiązkę poruszającą się po linii prostej. Z tego, w którym miejscu nastąpiło pierwsze odbicie, wiemy, że laser porusza się o w górę za każdym razem, gdy porusza się w prawo. Po jakimś czasie uderzy on w narożnik jednego z oditych pokojów i, przy odrobinie szczęścia, będzie to narożnik w którym będzie znajdował się balonik (lub jedna z jego odbitych wersji).

Laser uderza w róg pokoju, gdy zarówno jego droga przebyta w górę jak i droga przebyta w prawo są całkowitymi wielokrotnościami . Jeśli wiązka przebyła w prawo, to wiemy, że przebyła w górę. Jeśli jest liczbą naturalną, to jest wielokrotnością . Musimy zatem znaleźć najmniejsze takie , że jest wielokrotnością . Ponieważ , to najmniejszym takim jest . Powyższe rozważania obrazuje następujący rysunek:

Z tego rysunku wynika również, że laser rzeczywiście po pewnym czasie trafi w róg, w którym znajduje się balonik. Pozostaje nam policzyć odbicia. W naszym podejściu każdemu odbiciu się od ściany odpowiadało przecięcie lini promienia ze ścianą jednego z lustrzanych pokoi. Na rysunku możemy zobaczyć, że wiązka przeszła przez poziomą ścianę razy, a przez pionową ścianę – razy. Zatem wiązka przecina ściany odbitych pokoi razy. Ta sytuacja odpowiada temu, że w wyjściowym pokoju laser odbił się razy przed uderzeniem w balonik.

Uwaga: Poniższy rysunek pokazuje jak dokładnie wyglądał tor wiązki przed trafieniem w balonik:

Wynik:

Po umieszczeniu mąki o masie w mniejszej szklance o polu podstawy równym ciężar tejże szklanki (wraz z zawartością) wzrósł o . Musiała się zatem zwięszyć działająca nań siła wyporu, co mogło mieć miejsce tylko poprzez zwiększenie objętości wypieranej cieczy. Żeby obliczyć tę zmianę, używamy wzoru Archimedesa , gdzie to zmiana zanurzonej objętości. Pod wpływem większego ciężaru dno mniejszej szklanki zbliży się do dna większej o odległość . Wyparta zostanie wtedy dodatkowa objętość wody równa , która musi się gdzieś przemieścić ( to pole podstawy mniejszej szklanki). Spowoduje to podniesienie się poziomu wody o . Objętość przemieszczonej wody można wyrazić jako , gdzie jest polem podstawy większej szklanki. Porównując objętości otrzymujemy równanie: gdzie jest polem podstawy większej szklanki. W wyniku tych dwóch ruchów głębokość zanurzenia małej szklanki wzrośnie o . Zatem zmiana zanurzonej objętości wyniesie Łącząc uzyskane wzory: Zatem poziom tafli wody podniósł się o

Wynik:

Bezpośrednie dodawanie takiej liczby dziewiątek byłoby dość trudne. Znajdźmy więc inny sposób na obliczenie sumy danych liczb. Zauważmy, że po dodaniu do każdej z tych liczb dostajemy liczbę z jedynką na pierwszej pozycji i zerami na kolejnych pozycjach. Mamy zatem równość

Suma wszystkich wynosi . Pozostałe składniki sumują się do liczby gdzie wszystkich jedynek jest . Liczba otrzymana przez Zuzię to właśnie ta duża liczba pomniejszona o 2022.

Odjęcie będzie miało wpływ wyłącznie na ostatnich cyfr liczby. Zostaną one zamienione na . Pozostałe cyfr pozostanie niezmienione. Wynika stąd, że suma cyfr liczby Zuzi wynosi .

Wynik:

Oznaczmy wymiary cegły przez , , i jej masę przez . Wtedy ciśnieni a , and dane w treści zadania można obliczyć z następujących zależności: Po przemnożeniu wszystkich równań dostajemy: Jak widać, to objętość cegły . Powyższe równanie może być przekształcone: Pozostaje jedynie zauważyć, że to gęstość cegły . Używając tej wiedzy znajdujemy masę cegły: Masa cegły wynosi .

Wynik:

Niech będzie przecięciem prostych i . Ponieważ proste i są równoległe, to trójkąty i są podobne. Stosunek długości odpowiadających sobie boków w tych trójkątach wynosi . To daje nam równania: Ponadto wiemy, że oraz . Podstawiając do uzyskanych wcześniej równań dostajemy: W trójkącie zachodzi równość , więc z twierdzenia odwrotnego do twierdzenia Pitagorasa dostajemy, że jest to trójkąt prostokątny z kątem prostym przy wierzchołku . Wobec tego trójkąt również jest prostokątny. Pole powierzchni trapezu jest równe różnicy pól tych dwóch trójkątów.

Przyprostokątne trójkąta mają długości i , więc pole tego trójkąta wynosi . Trójkąt ma przyprostokątne długości i , więc jego pole jest równe .

Stąd pole trapezu wynosi .

Wynik:

Zacznijmy od rozwiązania prostszego problemu w którym Tadeusz zaznacza tylko 4 punkty. Oznaczmy je przez i załóżmy, że leżą one na okręgu w takiej właśnie kolejności. Ponieważ narysowane odcinki nie mogą mieć wspólnych końców, to wystarczy rozważyć poniższe 3 możliwości ich narysowania (3 możliwe podziały punktów na rozłączne pary):

1. odcinek i ,

2. odcinek i ,

3. odcinek i .

W drugim przypadku odcinki się przecinają, a w pozostałych nie. Zatem dla czterech zaznaczonych punktów mamy dwie możliwości narysowania odcinków.

Wróćmy teraz do oryginalnego problemu, czyli 13 zaznaczonych punktów. 2 wybrane odcinki mają łącznie 4 różne końce. Z wcześniejszych rozważań wiemy, że dla każdej czwórki punktów istnieją dokładnie dwa poprawne sposoby narysowania odcinków.

Pozostaje tylko wyznaczyć liczbę sposobów, na którą można wybrać punkty spośród . Pierwszy punkt można wybrać na sposobów, drugi na , trzeci na i czwarty na . Wybierając w ten sposób możemy jednak wybrać tę samą czwórkę kilka razy ( i to ta sama czwórka). Musimy wyznaczyć liczbę sposobów wybrania ustalonej czwórki. Decydujemy, który element wybieramy jako pierwszy. Są na to 4 możliwości. Na wybór drugiego elementu mamy 3 możliwości, trzeciego 2 i czwartego 1. Zatem każdą czwórkę można wybrać na sposobów. Ostatecznie liczba wszystkich możliwych czwórek wynosi .

Pamiętając, że dla każdej czwórki można narysować odcinki na dwa różne sposoby, dostajemy, że liczba wszystkich sposobów wynosi .

Wynik:

Oznaczmy masy klocków przez , , i współczynnik tarcia przez . Rozważmy siły działające na poszczególne klocki. Wyglądają one następująco:

Siły , i są ciężarami poszczególnych klocków. Ponadto klocki oddziałują na siebie siłami nacisku i . Górny klocek działa na środkowy z siłą skierowaną w dół. W tym samym czasie, na mocy trzeciej zasady dynamiki Newtona środkowy działa na górny z siłą o tej samej wartości skierowaną w górę . Podobnie sprawa wygląda pomiędzy środkowym i dolnym klockiem z siłą o wartości . Ponadto podłoże działa na dolny klocek z siłą .

Siły działające w kierunku poziomym to siła z którą Maja ciągnie linę, a także siły i odpowiadające naprężeniom w linie. Ponadto mamy jeszcze siły tarcia. Na górny klocek, który chciałby poruszyć się w prawo, działa siła skierowana w lewo. Ponownie z trzeciej zasady dynamiki Newtona wnioskujemy, że górny klocek musi działać na środkowy z siłą o wartości , ale skierowaną w prawo. Podobna sytuacja zachodzi dla środkowego i dolnego klocka. Ponadto podłoże działa na dolny klocek z siłą tarcia .

Aby układ pozostawał w spoczynku, siły działające na każdy prostopadłościan i w każdym kierunku muszą się sumować do 0. Dla kierunku pionowego otrzymujemy równania: Tymczasem dla kierunku poziomego dostajemy: Ciężary można policzyć ze wzoru , gdzie to standardowe przyspieszenie ziemskie. Kiedy Maja pociąga z największą możliwą siłą, siły tarcia statycznego również muszą być maksymalne - gdyby Maja użyła nieco większej siły to cały układ poruszyłby się i siły tarcia działałyby z największą możliwą wartością. Wartość ta może być obliczona ze wzoru . Pozostaje wyznaczyć nieznane wartości używając sześciu powyższych równań: W związku z tym, największa siła jakiej może użyć Maja, ma wartość: