Wynik:

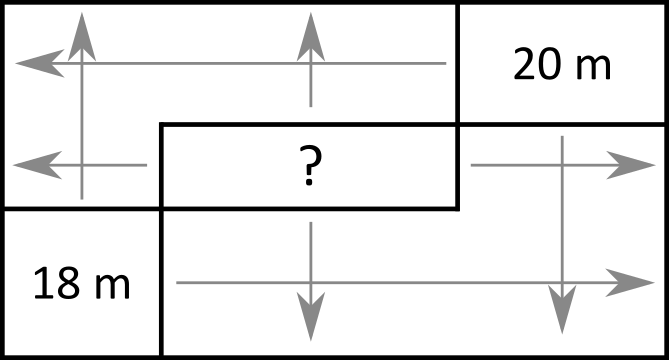
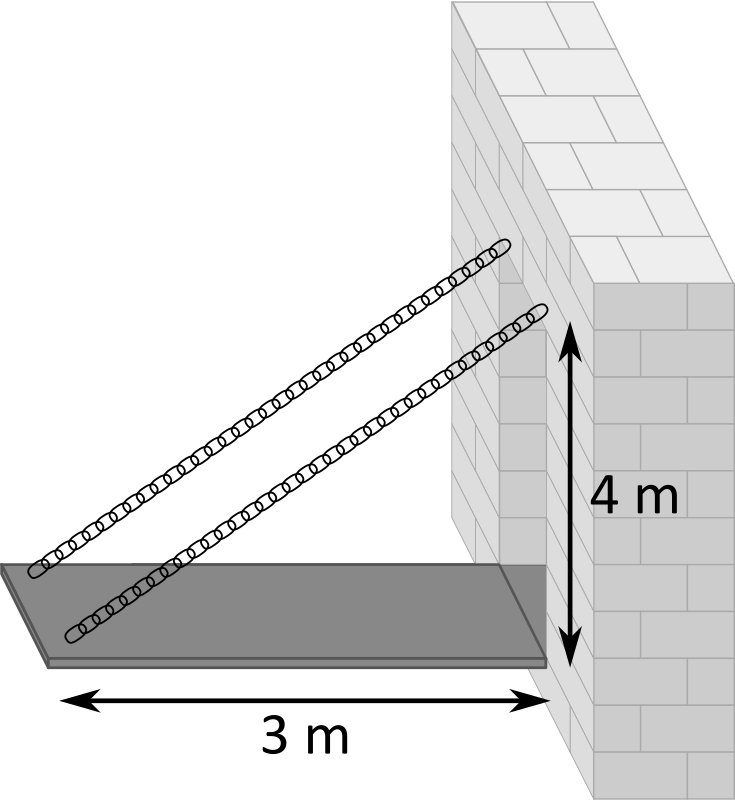
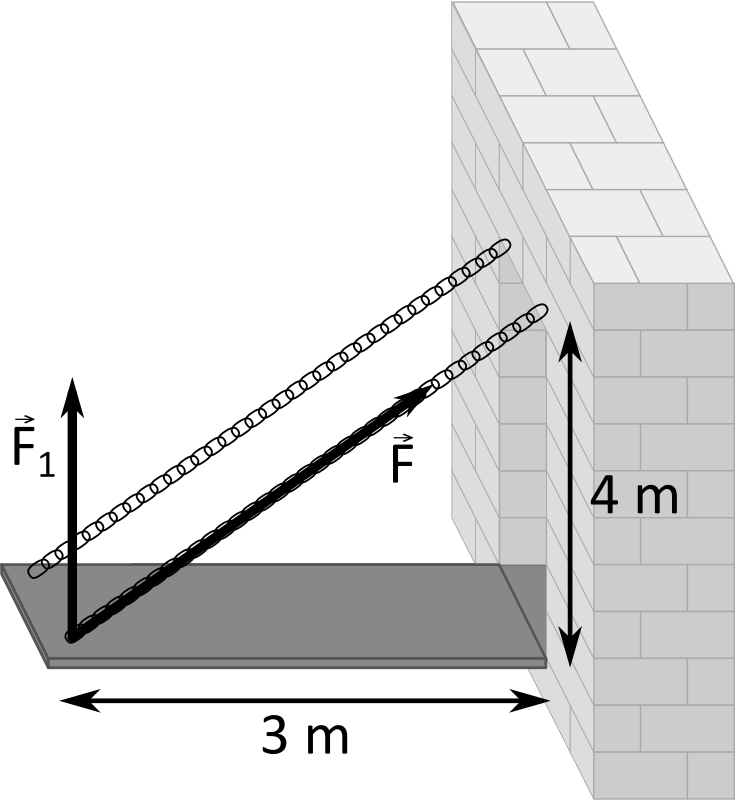
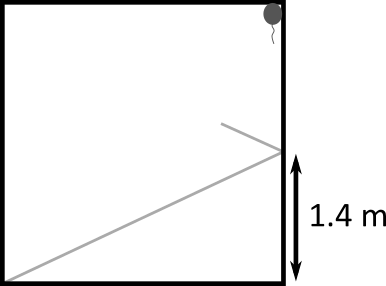
Gdy spróbujemy narysować kilka pierwszych odbić, przekonamy się, że wiązka odbije się stosunkowo dużo razy, zanim trafi w balonik. Za każdym razem musielibyśmy również liczyć, w którym dokładnie miejscu laser odbija się od ściany, co nie jest proste. Zastosujmy zatem inne podejście.
Zamiast przerzucać wiązkę względem lini prostopadłej do ściany w punkcie odbicia, przerzucimy cały pokój względem ściany, od której odbił się laser. Załóżmy zatem, że po drugiej stronie prawej ściany naszego pokoju jest drugi pokój będący jego lustrzanym odbiciem, Jeśli pozwolilibyśmy promieniowi przechodzić przez ściany pomieszczenia, w lustrzanej wersji naszego pokoju miałby on taki sam przebieg, jak w wyjściowym pokoju, gdyby odbił się od ściany. Powtarzając ten proces wielokrotnie, odbijając pokoje względem ścian, w które uderzył promień lasera, uzyskujemy wiązkę poruszającą się po linii prostej. Z tego, w którym miejscu nastąpiło pierwsze odbicie, wiemy, że laser porusza się o  w górę za każdym razem, gdy porusza się
w górę za każdym razem, gdy porusza się  w prawo. Po jakimś czasie uderzy on w narożnik jednego z oditych pokojów i, przy odrobinie szczęścia, będzie to narożnik w którym będzie znajdował się balonik (lub jedna z jego odbitych wersji).
w prawo. Po jakimś czasie uderzy on w narożnik jednego z oditych pokojów i, przy odrobinie szczęścia, będzie to narożnik w którym będzie znajdował się balonik (lub jedna z jego odbitych wersji).
Laser uderza w róg pokoju, gdy zarówno jego droga przebyta w górę jak i droga przebyta w prawo są całkowitymi wielokrotnościami  . Jeśli wiązka przebyła
. Jeśli wiązka przebyła  w prawo, to wiemy, że przebyła
w prawo, to wiemy, że przebyła  w górę. Jeśli
w górę. Jeśli  jest liczbą naturalną, to
jest liczbą naturalną, to  jest wielokrotnością
jest wielokrotnością  . Musimy zatem znaleźć najmniejsze takie
. Musimy zatem znaleźć najmniejsze takie  , że
, że  jest wielokrotnością
jest wielokrotnością  . Ponieważ
. Ponieważ  , to najmniejszym takim
, to najmniejszym takim  jest
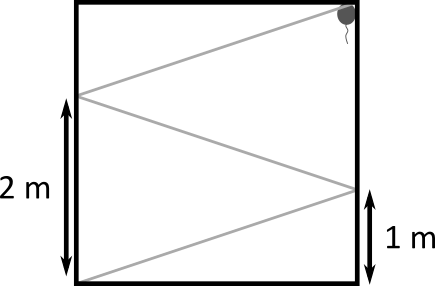
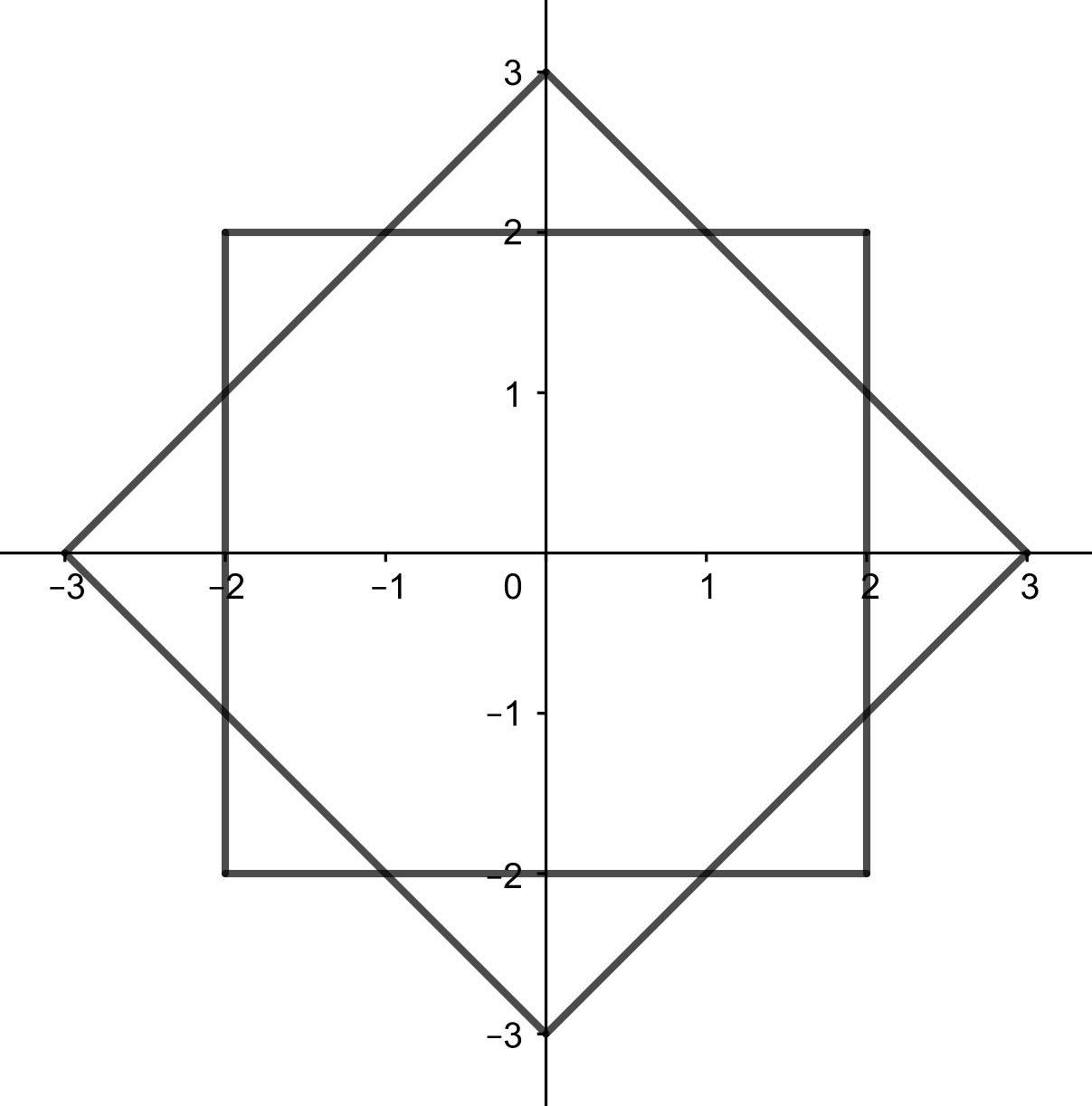
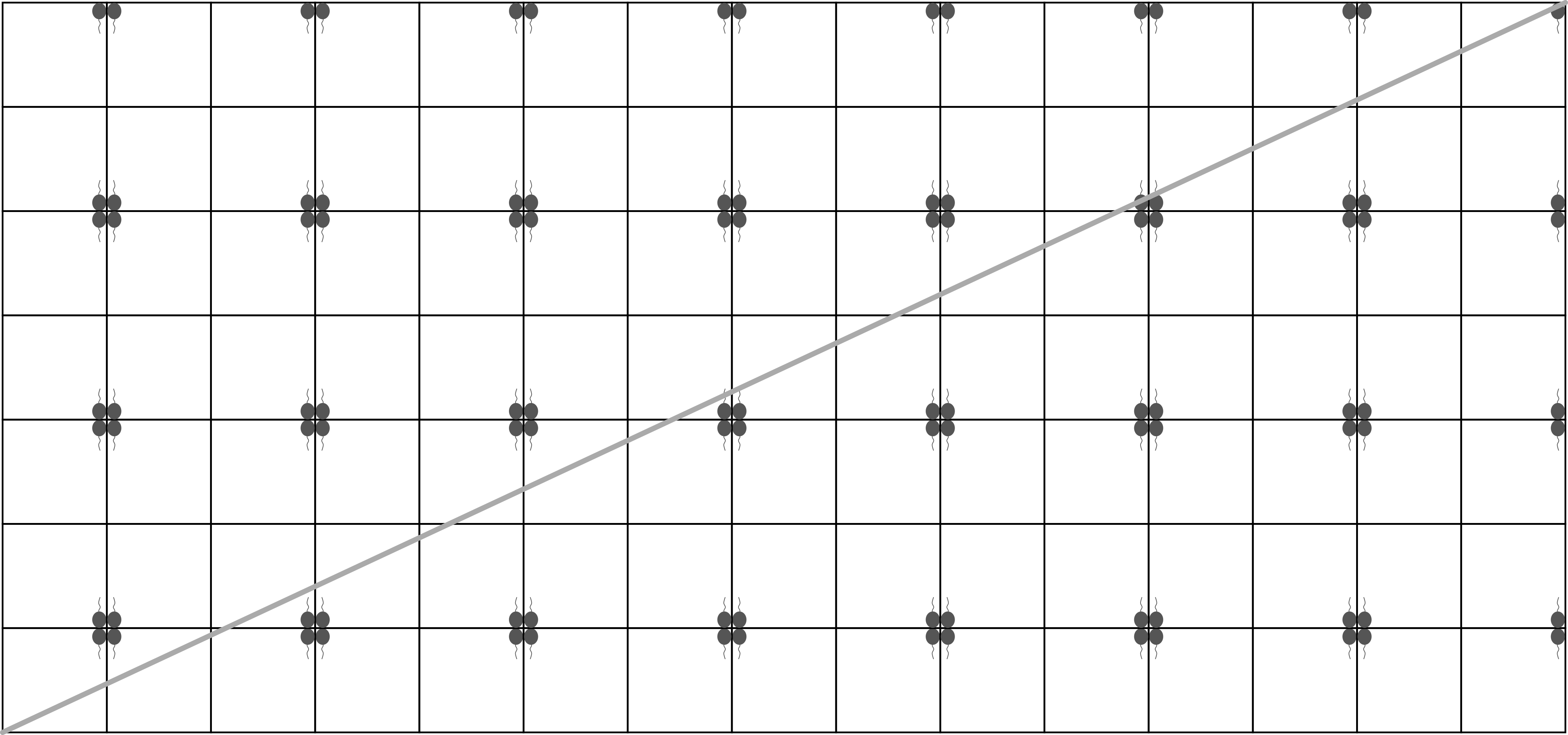
jest  . Powyższe rozważania obrazuje następujący rysunek:
. Powyższe rozważania obrazuje następujący rysunek:
Z tego rysunku wynika również, że laser rzeczywiście po pewnym czasie trafi w róg, w którym znajduje się balonik. Pozostaje nam policzyć odbicia. W naszym podejściu każdemu odbiciu się od ściany odpowiadało przecięcie lini promienia ze ścianą jednego z lustrzanych pokoi. Na rysunku możemy zobaczyć, że wiązka przeszła przez poziomą ścianę  razy, a przez pionową ścianę –
razy, a przez pionową ścianę –  razy. Zatem wiązka przecina ściany odbitych pokoi
razy. Zatem wiązka przecina ściany odbitych pokoi  razy. Ta sytuacja odpowiada temu, że w wyjściowym pokoju laser odbił się
razy. Ta sytuacja odpowiada temu, że w wyjściowym pokoju laser odbił się  razy przed uderzeniem w balonik.
razy przed uderzeniem w balonik.
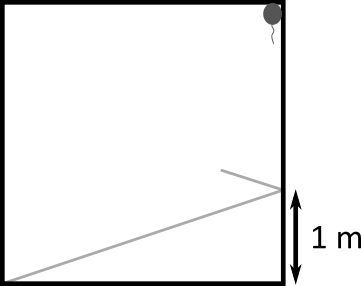
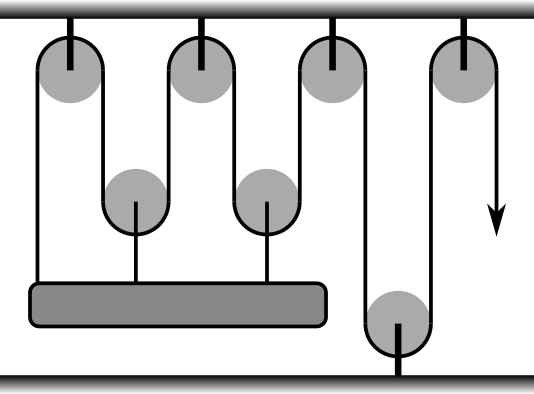
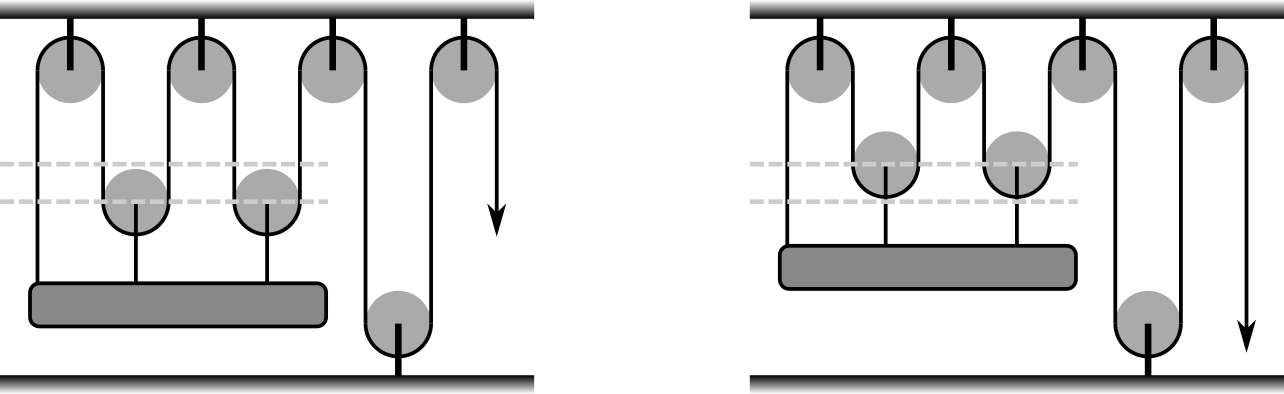
Uwaga: Poniższy rysunek pokazuje jak dokładnie wyglądał tor wiązki przed trafieniem w balonik:
. Każdego roku jabłoń rosła o dodatkowe
. Jaka jest wysokość jabłoni w centymetrach tego samego dnia w 2022 roku?
. Przez następne 10 lat, jabłoń rosła o dodatkowe
rocznie. Tak więc jej wysokość w roku 2022 wynosi
.