Zadania

Wynik:

$27$

Gdy Asia przekazała Bartkowi jedenaście spośród swoich kamyków, straciła $11$ kamyków, a Bartek zyskał ich $11$. Zatem różnica pomiędzy liczbą kamyków, które posiadali, zmalała o $11+11=22$. Zatem na końcu Asia miała $49-22=27$ więcej kamyków niż Bartek.

Wynik:

$5$

Pierwsze trzy miesiące $2023$ roku mają kolejno $31$, $28$ i $31$ dni. Razem stanowi to $31+28+31=90$ dni, czyli $90\cdot 24=2160$ godzin. Zatem Teresa przejechała $10800$ kilometrów w ciągu $2160$ godzin. W takim razie, jej średnia szybkość musiała wynieść $\frac{10800\mathrm{km}}{2160h}=5\mathrm{km}∕h$.

Wynik:

$56$

Aby narysować cztery kwadraty na dole, Laura potrzebuje $13$ odcinków. Dodanie kolejnych trzech kwadratów wymaga $7$ odcinków. Kolejne dwa kwadraty wymagają kolejnych $5$ odcinków. Na końcu, aby narysować kwadrat na samej górze, Laura musi dorysować jeszcze $3$ odcinki. Sumarycznie, potrzeba $13+7+5+3=28$ odcinków. Każdy z nich ma długość $2\mathrm{cm}$, więc ich sumaryczna długość wynosi $28\cdot 2\mathrm{cm}=56\mathrm{cm}$.

Wynik:

$45$

Zaglądając do karty ze wzorami możemy dowiedzieć się, że $36\mathrm{oz}$ to tyle samo co $1l$. W takim razie, objętość puszki w litrach to $\frac{12\mathrm{oz}}{36\mathrm{oz}∕l}=\frac{1}{3}l$. Oznacza to, że w litrze coli znajduje się $3\cdot 150=450$ kilokalorii, zaś w $100\mathrm{ml}$ coli jest $450:10=45$ kilokalorii.

Wynik:

$7$

Gdyby w skrzyni było 48 monet mniej, każda osoba otrzymałaby $6$ monet mniej, niż faktycznie otrzymała. W takim razie, w załodze musi być $48:6=8$ osób. Skoro mamy nie liczyć Antoniego, to poprawna odpowiedź wynosi $8-1=7$.

Wynik:

$4620$

Podczas $18$-minutowego treningu, Andrzej wykona $18:3=6$ okrążeń. Każde z jego okrążeń ma długość $2\pi \cdot 70m=140\pi m$. Oznacza to, że przebiegnie łącznie $6\cdot 140\pi m=840\pi m$ i wykona tyle samo kroków. Podobnie, Zuza wykona $18:2=9$ okrążeń długości $2\pi \cdot 35m=70\pi m$. Przebiegnie łącznie dystans $9\cdot 70\pi m=630\pi m$ i wykona taką właśnie liczbę kroków. Sumarycznie, wykonają $840\pi +630\pi =1470\pi$ kroków. Jeśli użyjemy przybliżenia $\pi =\frac{22}{7}$, obliczymy że wykonali oni $1470\cdot \frac{22}{7}=4620$ kroków.

Jeśli założymy $\pi =3,14$, otrzymamy wynik $4615,8$, który po zaokrągleniu do dziesiątek daje taką samą odpowiedź.

Wynik:

$9$

Żeby otworzyć drzwi z jak najmniejszą siłą, musimy sprawić, by momenty sił działające na te drzwi równoważyły się. Moment siły $M$ wywieranej przez zamykacz jest równy iloczynowi tej siły i odległości punktu jej przyłożenia od zawiasów: $M=48N\cdot 15\mathrm{cm}=720N\mathrm{cm}$. Używając tego samego równania, wnioskujemy, że Olek musi działać na drzwi siłą $F$ w odległości $a=80\mathrm{cm}$ od zawiasów:

Wynik:

$6,28$

Jeśli Ziemia jest idealną kulą, oplatająca ją lina będzie tworzyła idealny okrąg. Jeśli promień tego koła to $r$, Ewa będzie potrzebowała liny o długości $2\mathit{\pi r}$. Adam będzie potrzebował utworzyć z liny okrąg o promieniu $r+1m$, więc jego lina będzie musiała mieć długość $2\pi (r+1m)$. Różnica długości lin Adama i Ewy wyniesie zatem $2\pi (r+1m)-2\mathit{\pi r}=2\pi m\doteq 6,28m$.

Wynik:

$5$

Za każdym razem, gdy promień uderza w lustro, zmienia swój kierunek o $90^{\circ }$ w prawo lub w lewo (zależnie od ustawienia lustra). Łatwo znaleźć poniższy sposób na rozwiązanie zagadki za pomocą tylko $5$ odbić promienia (ustawienia luster nieprzedstawionych na ilustracji nie mają znaczenia).

Z drugiej strony, można zauważyć, że nie jest możliwe, by światło odbiło się tylko $3$ razy (promień musiałby nie zmienić kierunku w niektórych polach). Dodatkowo, widać, że potrzebna jest nieparzysta liczba odbić - po nieparzystej liczbie odbić kierunek promienia jest pionowy, zaś po parzystej liczbie odbić kierunek jest poziomy.

W takim razie, liczba odbić musi być nieparzystą liczbą większą od $3$, co oznacza, że istotnie $5$ jest minimalną potrzebną liczbą odbić.

Wynik:

$45$

Używając wyłącznie cyfry $1$ możemy utworzyć $5$ szorstkich liczb w danym w zadaniu zakresie: $11$, $111$, $1111$, $11111$ i $111111$. Podobnie możemy utworzyć pięć szorstkich liczb używając każdej z cyfr od $2$ do $9$ ale nie możemy utworzyć żadnej szorstkiej liczby z cyfry $0$. Wobec tego istnieje dokładnie $9\cdot 5=45$ szorstkich liczb większych od dziesięciu i mniejszych od miliona.

Wynik:

$1$

Suma wszystkich liczb wpisanych w pola planszy to $0+1+2+3+4+5+6=21$. Oznacza to, że suma liczb w każdej kolumnie musi wynosić $21:3=7$. Można zauważyć, że liczba $0$ nie może występować w pierwszej ani ostatniej kolumnie, ponieważ musielibyśmy użyć liczby $7$, której nie mamy do dyspozycji. W takim razie $0$ zawsze musi być wpisane w środkową kolumnę, co sprawia że iloczyn liczb w środkowej kolumnie musi zawsze być równy $0$. Zatem Daniel jest w stanie otrzymać tylko jeden iloczyn równy $0$.

Wynik:

$250$

Gdyby Przemek nie zapomniał zatkać odpływu to wanna napełniłaby się w czasie $150l:0,2l∕s=750s$. Ponieważ jednak odpływ jest otwarty, to łączna prędkość przyrostu objętości wody wynosi $0,2l∕s-0,05l∕s=0,15l∕s$. Wanna zostanie zatem napłniona w czasie $150l:0,15l∕s=1000s$, więc zajmie to $1000s-750s=250s$ dłużej.

Wynik:

$16$

Po pierwszym ruchu król może przemieścić się do każdego z pól zaznaczonych na obrazku:

Teraz pytanie jest takie: do ilu pól może przemieścić się król zaczynając z dowolnego położenia z poprzedniego obrazka? Łatwo zauważamy, że król może ruszyć się do dowolnego spośród tych 16 pól:

Wynik:

$14$

Dwa powstałe trójkąty mają po dwa boki takiej samej długości jak jakiś bok czworokąta oraz po jednym boku o długości równej długości przekątnej. Oznacza to, że suma ich obwodów jest równa obwodowi czworokąta powiększonemu o dwukrotność długości przekątnej. Różnica pomiędzy sumą obwodów trójkątów a obwodem czworokąta wynosi $77\mathrm{cm}-49\mathrm{cm}=28\mathrm{cm}$, zatem długość przekątnej to $28\mathrm{cm}:2=14\mathrm{cm}$.

Wynik:

$10$

Po rzucie pozioma składowa prędkości piłki będzie równa $9\mathrm{km}∕h=2,5m∕s$ podczas gdy Sławka przyspieszy do prędkości $18\mathrm{km}∕h=5m∕s$. Wobec tego względna prędkość w poziomie pomiędzy Sławką a jej piłką będzie wynosić $5m∕s-2,5m∕s=2,5m∕s$. Zatem po $4$ sekundach, kiedy piłka uderzy w ziemię, Sławka będzie w odległości $2,5m∕s\cdot 4s=10m$ od swojej piłki.

Wynik:

CDAB

Zaczniemy od ustalenia, która w kolejności była Alicja. Skoro wszystkie zdania są fałszywe, Alicja nie mogła być druga. Beata i Celina przybyły kolejno po Alicji i przed nią, więc Alicja nie mogła przybyć ani jako pierwsza, ani jako ostatnia. Musiała być zatem trzecia. Beata skłamała, że przyszła przed Alicją, zatem musiała przybyć po niej. To oznacza, że przyszła jako ostatnia. Daria nie przyszła jako pierwsza, więc musiała przyjść jako druga. Jedynym pozostałym miejscem dla Celiny jest pierwsze miejsce, i łatwo stwierdzić, że przyszła przed Alicją, a zatem rzeczywiście zdanie wypowiedziane przez nią było nieprawdziwe. To oznacza, że dziewczyny przybyły w kolejności: Celina, Daria, Alicja i Beata.

Wynik:

$5$

Obliczmy okres między odjazdamy tramwaju nr 12. Gdy Jarda jedzie tramwajem, jego prędkość względem mijanego tramwaju jest dwa razy większa niż prawdziwa szybkośc pojazdu. Zatem z jego perspektywy przemierza stałą odległość między dwoma mijanymi tramwajami w czasie dwa razy krótszym niż w rzeczywistości, zatem prawdziwa odległość między dwoma odjazdami tramwaju nr $12$ z przystanku jest dwa razy dłuższa niż obserwuje to Jarda. Zatem linia nr $12$ kursuje co $2\cdot 2=4$ minuty. W ciągu godziny na przystanku zatrzyma się $60:4=15$ tramwajów nr $12$.

Podobnie, w ciągu godziny z jednego przystanku odjedzie $60:6=10$ tramwajów nr $5$. Zatem w ciągu godziny na przystanku zatrzyma się o $15-10=5$ tramwajów nr $12$ więcej niż tramwajów nr $5$.

Wynik:

$250$

Musimy się zastanowić, jak tarcie wpływa na ruch pudła. Siłą tarcia działa tylko między ciałami, które działają na siebie z pewną siłą nacisku. W naszym przypadku pudło nie naciska w żaden sposób na pionową ścianę, zatem na pudło nie zadziała siła tarcia. Zatem jednyną siłą (poza siłą wywieraną przez Boba), która działa na pudło jest siła ciężkości $F_g=\mathit{mg}$, gdzie $m=25\mathrm{kg}$ to masa pudła. Bob musi pociągnąć za linę z siłą $F$ o takiej samej wartości, zatem $F=\mathit{mg}=25\mathrm{kg}\cdot 10N∕\mathrm{kg}=250N$.

Wynik:

$50$

Karolina musi wziąc co najmniej $2$ dżemy malinowe, $5$ dżemów borówkowych, i po jednym dżemie jeżynowym, żurawinowym i truskawkowym. Pomyślmy, co może się zdarzyć, jeśli jeden z tych warunków nie jest spełniony. Jeśli Karolina nie zabiere $2$ dżemów malinowych to w najgorszym przypadku zabierze wszystkie inne dżemy i jeden dżem malinowy. To daje razem $1+15+7+15+9=47$ dżemów. Jeśli wzięłaby $48$ dżemów, problem by nie wystąpił. Podobnie, problem pojawiłby się, gdyby wzięła $4$ dżemy borówkowe i wszystkie dżemy pozostąłych typów – razem $10+4+7+15+9=45$ dżemów. Żeby temu zapobiec, musi wziąć ze sobą co najmniej $46$ dżemów. Jeśli powtórzymy to rozumowanie dla jeżyn, żurawiny i truskawek, wnioskujemy, że Karolina musi wziąć kolejno co najmniej $(10+15+0+15+9)+1=50$, $(10+15+7+0+9)+1=42$ lub $(10+15+7+15+0)+1=48$ dżemów. Łącząc te wnioski, otrzymujemy, że rozwiązaniem jest największa liczba spośród $48$, $46$, $50$, $42$, $48$. Zatem Karolina musi wziąć ze sobą co najmniej $50$ dżemów.

Wynik:

$64$

Niech $s$ oznacza długość trasy a $t$ będzie czasem, w jakim pokonał ją zwycięzca. Wiemy, że średnia szybkość zwycięzcy wynosiła $24\mathrm{km}∕h$, więc $\frac{s}{t}=24\mathrm{km}∕h$.

Dwie trzecie długości trasy stanowiły zjazdy, więc długość odcinków prowadzących w dół wynosiła $\frac{2}{3}s$. Ponadto, zwycięzca spędził $3$ razy więcej czasu na odcinkach podjazdowych, więc spędził na tych odcinkach $\frac{1}{4}t$. Średnia szybkość zwycięzcy na tych odcinkach wyniosła zatem:

Po podstawieniu $\frac{s}{t}=24\mathrm{km}∕h$ otrzymujemy, że ta średnia szybkość wyniosła:

Wynik:

$95$

Spójrzmy na ostatni rząd i drugą kolumnę. Muszą mieć one tę samą sumę, ale mają jedno wspólne pole. Zatem suma pól, które nie są dla nich wspólne również muszą być sobie równe. To oznacza, że suma liczb $15$ i $19$ jest taka sama jak suma liczb $16$ i liczby, którą trzeba wpisać w środkowe pole planszy. Ta suma wynosi $15+19=34$, czyli liczba wpisana na środku jest równa $34-16=18$.

Skoro na jednej z przekątnych zostały wpisane już wszystkie liczby, znamy już sumę pól w każdej kolumnie, każdym rzędzie i na każdej przekątnej – musi być ona równa $17+18+19=54$. Teraz łatwo możemy uzupełnić pozostałe pola tabeli:

Na koniec obliczamy sumę wszystkich wpisanych przez nas liczb: wynosi ona $21+22+18+14+20=95$.

Wynik:

$0,8$

Każdy metr drutu możemy zastąpić opornikiem o oporze równym $R_0=0,1\mathrm{\Omega }$. Gdy tak zrobimy, uzyskamy następujący schemat:

Możemy teraz wykorzystać klasyczne wzory na całkowity opór oporników połączonych równolegle i szeregowo, żeby obliczyć, że opór między punktami $A$ i $B$ wynosi:

Wynik:

$5$

Woda o objętości $V=150\mathrm{hl}$ ma masę $m=V{\rho }_{\mathit{wody}}$. Aby podgrzać ją z temperatury $t_1=29\circ C$ do $t_2=33\circ C$ trzeba dostarczyć jej ciepła $Q=c_{\mathit{wody}}m(t_2-t_1)=c_{\mathit{wody}}V{\rho }_{\mathit{wody}}(t_2-t_1)$. To ciepło musi być równe energii dostarczonej przez panele słoneczne. Mają one moc $P_0=1,4\mathrm{kW}∕m^2$ na jednostkę powierzchni, więc jeśli łączna powierzchnia paneli wynosi $S$, to ich łączna moc wynosi $P=P_{0}S$. Po czasie $t=10h$ dostarczą one energię $W=\mathit{Pt}=P_0\mathit{St}$, mamy zatem równości:

Zatem Bożeka potrzebuje $5m^2$ paneli słonecznych.

Wynik:

$40$

Kolejność zdobywania goli można zapisać jako ciąg liter F i M gdzie F oznacza bramkę zdobytą przez fizyków, a M przez matematyków. Przy takich oznaczeniach widzimy, że jest $10$ możliwych kolejności zdobywania goli w pierwszej połowie: MMFFF, MFMFF, MFFMF, MFFFM, FMMFF, FMFMF, FMFFM, FFMMF, FFMFM, FFFMM. Podobnie mamy $4$ możliwe kolejności zdobycia czterech goli, które padły w drugiej połowie: FMMM, MFMM, MMFM, MMMF. Teraz możemy połączyć dowolną kolejność z pierwszej połowy z dowolną kolejnością z drugiej, co daje nam łącznie $10\cdot 4=40$ możliwych kolejności.

Wynik:

$125$

Jeśli robot naciska na ścianę z siłą $F$ to siła tarcia statycznego jest skierowana do góry i wynosi $F_f=\mathit{fF}$, gdzie $f=0,3$ to współczynnik tarcia statycznego. Z kolei ciężar robota wynosi $F_g=\mathit{mg}$ i jest skierowany w dół. Celem zapewnienia stabilności ciężar robota musi być równoważony przez siłę tarcia o każdą z czterech ścian dziury. Mamy zatem równości:

W związku z tym, siła $F$ wynosi:

Wynik:

$3$

Każdy sześciokąt może być podzielony na $6$ trójkątów równobocznych. To pozwala nam narysować trójkątną siatkę wewnątrz równoległoboku:

Z tego od razu widać, że długość boku sześciokąta (która jest taka sama jak długość boku każdego z trójkątów) wynosi $12\mathrm{cm}:4=3\mathrm{cm}$.

Wynik:

$1100$

Statek zanurzy się całkowicie w momencie gdy siła grawitacji zostanie zrównoważona przez siłę wyporu. Maksymalna siła wyporu, która może działać na statek o objętości $V$ to $F_{\mathit{wyporu}}=V{\rho }_{\mathit{wody}}g$. Siłę ciężkości można podzielić na ciężar samego statku i ciężar wody, która do niego wpłynęła. Ciężar statku o masie $m$ wynosi $F_{g_1}=\mathit{mg}$. Woda wpływa do statku ze stałą prędkością $Q$, więc po czasie $t$ objętość wody w statku będzie wynosiła $V^{\prime }=\mathit{Qt}$. Ciężar wody po czasie $t$ wynosi zatem $F_{g_2}=\mathit{Qt}{\rho }_{\mathit{wody}}g$. Warunek na całkowite zanurzenie to $F_{\mathit{wyporu}}=F_{g_1}+F_{g_2}$, co pozwala nam znaleźć wzór na $t$:

Statek zatonie więc po czasie:

Wynik:

$1990$

Obaj chłopcy dodali do siebie liczby od roku w którym się urodzili aż do $2023$. Gaweł otrzymał wiekszy wynik, więc dodał do siebie pewne liczby, których nie dodał Paweł. Ponieważ każdy składnik sumy wynosi około $2000$, liczba składników które zostały dodane przez tylko przez Gawła to $19945:2000\doteq 10$. Oznacza to, że liczby dodane tylko przez Gawła to $x$, $x+1$, …, $x+9$, gdzie $x$ to rok urodzenia Gawła. Ich suma to $10x+45$. Otrzymujemy równanie $10x+45=19945$ z którego wyliczamy, że Gaweł urodził się w roku $x=\frac{19945-45}{10}=1990$.

Wynik:

$11$

Sprawdzamy możliwości grupując je po ustawieniu pierwszego i ostatniego lustra. Możliwe kombinacje są przedstawione w wierszach poniższego rysunku (dla przejrzystości, lustra, od których promień lasera się nie odbił nie zostały narysowane):

Tak więc widzimy $1+3+3+4=11$ możliwych trajektorii promienia lasera.

Wynik:

$\frac{68}{3}$

Zapiszmy długości boków prostokąta $\mathit{ABCD}$ jako $\mathit{AB}=9x$ i $\mathit{BC}=8x$ dla pewnego $x$, wyrażonego w centymetrach.

Obliczmy najpierw obwód czworokąta $\mathit{ABEF}$. Przyprostokątne trójkąta prostokątnego $\mathit{ECF}$ mają długości $4x$ i $3x$. Tak więc z twierdzenia Pitagorasa $\mathit{EF}=\sqrt{{(4x)}^2+{(3x)}^2}=5x$. Podobnie, przyprostokątne w trójkącie $\mathit{FDA}$ mają długości $6x$ i $8x$, czyli $\mathit{FA}=\sqrt{{(6x)}^2+{(8x)}^2}=10x$. Wobec tego, obwód czworokąta $\mathit{ABEF}$ wynosi $9x+4x+5x+10x=28x$.

Policzmy teraz pole czworokąta $\mathit{ABEF}$. Trójkąty prostokątne $\mathit{ECF}$ oraz $\mathit{FDA}$ mają pola $\frac{(4x)\cdot (3x)}{2}=6x^2$ i $\frac{(6x)\cdot (8x)}{2}=24x^2$. Pole prostokąta $\mathit{ABCD}$ wynosi $(9x)\cdot (8x)=72x^2$, czyli pole czworokąta $\mathit{ABEF}$ jest równe $72x^2-6x^2-24x^2=42x^2$. Wiemy że wartości długości obwodu i pola czworokąta $\mathit{ABEF}$ są równe, co oznacza że:

Pozostaje obliczyć obwód prostokąta $\mathit{ABCD}$, czyli $9x+8x+9x+8x=34x=34\cdot \frac{2}{3}\mathrm{cm}=\frac{68}{3}\mathrm{cm}$.

Wynik:

$2$

Praca wykonana przez dżdżownicę będzie równa maksymalnej energii potencjalnej, jaką będzie miała dżdżownica podczas wspinaczki (zakładamy, że początkowo energia potencjalna będzie wynosić $0$). Nietrudno zauważyć, że maksymalna energia zostanie osiągnięta dokładnie wtedy, gdy dżownica ustawi się tak jak na rysunku dołączonym do zadania (im więcej ciała dżdżownicy znajduje się wyżej, tym wyższa jest jej energia potencjalna).

Podzielmy dżdżownicę na $3$ części (bez obaw, dżdżownicę potrafią się regenerować) – dwie cześci pionowe i jedną część poziomą, jak na rysunku z zadania. Wszystkie te części mają długość $10\mathrm{cm}$ – jedną trzecią długości ciała dżdżownicy. Dżdżownica jest jednorodna, więc każdy z fragmentów będzie miał masę $m_0=3g:3=1g$. Fragment poziomy ma swój środek masy w punkcie o wysokości $h_2=10\mathrm{cm}$, więc energia potencjalna tej części wyniesie $E_2=m_{0}g{h}_2=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,1m=0,001J=1\mathrm{mJ}$. Pionowe fragmenty mają swój środek masy na wysokości $h_1=h_3=5\mathrm{cm}$, więc ich energie potencjalne to $E_1=E_3=m_{0}g{h}_1=m_{0}g{h}_3=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,05m=0,0005J=0,5\mathrm{mJ}$.

Zatem maksymalna energia potencjalna dżdżownicy wyniesie $E=E_1+E_2+E_3=0,5\mathrm{mJ}+1\mathrm{mJ}+0,5\mathrm{mJ}=2\mathrm{mJ}$ i taką pracę będzie musiała wykonać dżdżownica.

Wynik:

$1050$

Możemy podzielić problem na mniejsze, łatwiejsze części. Zastanówmy się najpierw, ile prób potrzebujemy, żeby dojść do kombinacji ABA? Skoro alfabet ma $26$ liter, będziemy potrzebowali zmienić ostatni znak $26$ razy. A co z $\mathit{BAA}$? Po każdych $26$ próbach przedostatnia litera zmienia się na kolejną w alfabecie. Zatem, żeby przejść z AAA do BAA, potrzebujemy $26\cdot 26=676$ prób. Żeby przejść z BAA do BOA, będziemy potrzebować $26\cdot 14=364$ prób, bo O jest piętnastą literą alfabetu, i będziemy musieli wypróbować wcześniej $14$ poprzedzających liter. W końcu, skoro J jest dziesiątą literą alfabetu, będziemy potrzebowali jeszcze dziesięciu prób, żeby przejść z BOA do BOJ. Razem będziemy potrzebowali $676+364+10=1050$ prób.

Wynik:

$125$

Mechanizm jest w stanie spoczynku tylko jeśli działające na niego momenty sił znoszą się. Musimy zatem spojrzeć na momenty sił działające na dźwignie. Na każdy sznurek będzie działać pewne naprężenie, zatem sznurek będzie działał na każdą dźwignię z taką samą siłą równą temu naprężeniu. Przykłądowo: sznurek łączący środkową i prawą dźwignię będzie działać z taką samą siłą na środkową dźwignię (w prawo) jak na prawą dźwignię (w lewo). Ponadto, sznurki są przywiązane do obydwu dźwigni w tej samej odległości od osi obrotu, więc momenty siły, które będą działać na obu sznurka końcach będą takie same.

Zatem, jeśli układ ma pozostać w stanie równowagi, dwie siły, z którymi Patryk działa na dźwignie muszą skutkować tym samym momentem siły. To prowadzi do równania:

Patryk musi zatem działać na lewą dźwignię z siłą: $125N$.

Wynik:

$2,15$

Niech długości odcinków i nazwy punktów będą takie, jak na rysunku.

Rozważmy trójkąty prostokątne $\mathit{ABP}$ i $\mathit{ACP}$, i napiszmy dla nich wypowiedź twierdzenia Pitagorasa.

Jeśli wyznaczymy $h^2$ z poprzednich równań i przyrównamy do siebie prawe strony, otrzymamy:

Możemy teraz wykorzystać wzór skróconego mnożenia $a^2-b^2=(a-b)(a+b)$ i otrzymać:

Ale wiemy, że $y+x=20\mathrm{cm}$. Zatem różnica długości $y-x$, którą musimy wyznaczyć, wynosi:

Wynik:

$75$

Niech $m$ to masa wagonika, $r=30m$ promień pętli, a $v$ szybkość wagonika w najwyższym punkcie pętli.

Z pierwszej części zadania wiemy, że w najwyższym punkcie pętli działa siła dośrodkowa $F_c=\frac{m{v}^2}{r}$. Są dwie siły, które działają w tym kierunku - siła grawitacji $F_g=\mathit{mg}$ i pewna siła wynikająca z jazdy po łuku w pętli. Chcemy by ta siła dośrodkowa była jak najmniejsza (czym jest ona większa, tym większa musi być szybkość wagonika, a co za tym idzie i początkowa wysokość). Ponieważ nie możemy pozbyć się siły grawitacji, w przypadku granicznym zachodzi $F_c=F_g$. Z tego wynika

Z początku wagonik ma jedynie energię potencjalną grawitacji $E_1=\mathit{mgh}$. W najwyższym punkcie pętli ma zarówno energię potencjalną jak i kinetyczną. Znajduje się wtedy na wysokości $2r$ i porusza się z szybkością $v$, więc jego energia w tym punkcie to $E_2=\mathit{mg}(2r)+\frac{1}{2}m{v}^2$. Z zasady zachowania enegrii wynika że $E_1=E_2$. Korzystając z równania na $v^2$ zachodzi:

Stąd minimalna wysokość to

.

Wynik:

$23$

Rozwiązanie naturalnie rozdziela się na dwie części: w pierwszej z nich pokażemy, że gracze mogli rozegrać $23$ mecze, w drugiej – że jeśli gracze rozegraliby $24$ mecze, istniałaby grupa spełniająca warunki z treści zadania.

Część pierwsza: ponumerujmy graczy liczbami $1$, $2$, …, $24$. Niech mecze rozegrają się pomiędzy graczami nr $1$ i $2$, $2$ i $3$, …, $23$ i $24$. Wybierzmy dowolną grupę graczy. Znajdzmy w niej gracza o najmniejszym numerze, niech ten numer to $P$. W tej grupie gracz z numerem $P$ mógł podtencjalnie zagrać jedynie z graczem nr $P+1$, bo gracz z numerem $P-1$ nie mógł znaleźć się w grupie (miałby niższy numer niż gracz nr $P$). Zatem gracz nr $P$ nie zagrał z co najmniej dwoma innymi graczami ze wskazanej grupy. To rozumowanie działa dla każdej możliwej grupy, więc nie ma grupy spełniającej warunki zadania. Zatem gracze mogli rozegrać $23$ mecze.

Część druga: Musimy udowodnić, że jeśli rozegrano $24$ mecze, zawsze znajdzie się grupa graczy, która spełnia własność z zadania. Jeśli jakaś para graczy rozegrałaby ze sobą dwa mecze, moglibyśmy wybrać tą pare jako szukaną grupę. Zatem możemy założyć, że taka para nie istnieje.

Załóżmy, że każdy gracz rozegrał co najmniej $2$ mecze. Wybierzmy graczy w następujący sposób: zacznijmy od dowolnego gracza, nazwijmy go $P_0$. Zagrał on z innym graczem, powiedzmy $P_1$. Gracz $P_1$ zagrał z co najmniej $2$ różnymi graczami, więc zagrał z pewnym graczem $P_2$, który nie jest graczem $P_0$. Podobnie, $P_2$ zagrał z pewnym graczem $P_3$, który nie jest graczem $P_1$. W ten sposób znajdujemy kolejnych graczy. W pewnym momencie dojdziemy do gracza, którego już rozważaliśmy. Mamy wtedy pewną grupę graczy $P_k$, $P_{k+1}$, …, $P_n$ o własności, że każdy gracz $P_i$ zagrał z graczami $P_{i-1}$ i $P_{i+1}$ z tego ciągu, a gracze $P_k$ i $P_n$ również rozegrali mecz. Możemy zatem rozmieścić tych graczy na okręgu w ten sposób, że każdy gracz rozegrał mecz z dwoma graczami położonymi obok niego na okręgu. To oznacza, że znaleziona grupa spełnia warunki zadania.

Pozostaje nam rozważyć przypadek, w którym pewien gracz zagrał mniej niż $2$ mecze. Jeśli to prawda, możemy zignorować tego gracza. Wtedy będziemy mieli do rozważenia mniej graczy, ale liczba rozegranych przez nich meczy będzie ciągle niemniejsza od liczby graczy. Gdy zignorujemy jednego z graczy, albo okaże się, że każdy z pozostałych graczy rozegrał co najmniej dwa mecze, albo istnieje gracz, który rozegrał mniej niż dwa mecze. W pierwszym przypadku poprzednie rozumowanie udowadnia, że szukana grupa istnieje. W przeciwnym wypadku możemy zignorować kolejnego gracza. Postępując tak dalej, albo znajdziemy szukaną grupę, albo pozostanie jedynie $3$ graczy, którzy rozegrali między sobą co najmniej trzy mecze. To jest możliwe tylko wtedy, gdy każdy gracz grał z każdym, a to oznacza, że ci trzej gracze tworzą grupę, która spełnia warunki zadania.

To dowodzi, że jeśli rozegranoby $24$ mecze, Dora znalazłaby szukaną grupę.

Łącząc dwie części rozwiązania wnioskujemy, że maksymalna liczba rozegranych meczy wynosi $23$.

Wynik:

$25$

Najpierw musimy poznać zasadę podzielności przez $125$. Liczba jest podzielna przez $125$ jeśli liczba złożona z jej ostatnich trzech cyfr jest podzielna przez $125$ (jest to podobne kryterium do podzielności przez $2$, $4$, $8$, $16$ …, ale dla $5$, $25$, $125$ …). Dlaczego? Zapiszmy dowolną liczbę jako $1000A+B$, gdzie $B<1000$. W takim razie $B$ jest liczbą uformowaną z ostatnich trzech cyfr. Zauważmy, że $1000$ jest podzielne przez $125$, ponieważ $1000=8\cdot 125$. Zatem, by liczba $1000A+B$ była podzielna przez $125$, $B$ musi być podzielne przez $125$. To dowodzi kryterium podzielności przez $125$.

Teraz zastanówmy się, jakie ma to konsekwencje. Jedyne liczby składające się z co najwyżej $3$ cyfr podzielne przez $125$ to $0$, $125$, $250$, $375$, $500$, $625$, $750$, oraz $875$. Żadna z nich nie zaczyna się cyfrą $4$. Oznacza to, że wielokrotności $125$ nie mogą mieć liczby setek równej $4$.

Powróćmy do oryginalnego problemu. Wiemy, że liczba setek wynosi $4$, więc wynik Lucyny nie może być wielokrotnością $125$. Jeśli nie ominęłaby żadnej liczby, ostateczny wynik byłby podzielny przez $5\cdot 15\cdot 25$. Zatem rozkład na czynniki pierwsze iloczynu zawierałby liczbę $5$ cztery razy. To oznacza, że musimy usunąć $5$ co najmniej dwa razy. Jest to możliwe tylko przy pominięciu liczby $25$. Zatem Lucyna musiała pominąć liczbę $25$.

Wynik:

$28$

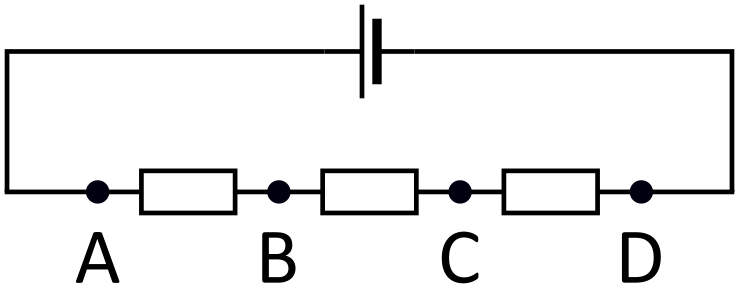
Napięcie pomiędzy dwoma punktami opisuje wartość różnicy potencjałów w tych punktach. Potencjał opisuje jedynie (elektryczną) energię potencjalną cząstki o ładunku $1C$. W każdym z punktów $A$, $B$, $C$ i $D$, ta cząstka miałaby pewną energię potencjalną więc każdemu z punktów możemy przypisać pewną wartość liczbową. Napięcia w takim spojrzeniu wyrażają jedynie różnice pomiędzy poszczególnymi wartościami.

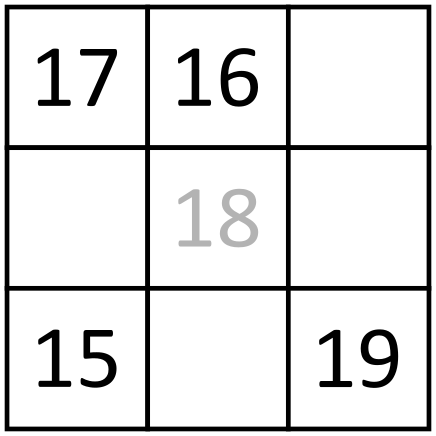
Możemy przeformułować ten problem do zadania matematycznego, gdzie mamy przypisać cztery wartości liczbowe do $A$, $B$, $C$ i $D$ (zauważmy, że teraz te litery nie mają nic wspólnego z punktami na obwodzie), tak by różnice pomiędzy nimi wynosiły $7$, $8$, $10$, $15$, $18$ i pewna nieznana, szukana wartość. Zauważmy pewną zależność. Rozważmy dowolną uporządkowanej trójkę $X$, $Y$ i $Z$, $X>Y>Z$. Różnica $X-Z$ jest sumą różnic $X-Y$ oraz $Y-Z$ (bo oczywiście $(X-Y)+(Y-Z)=X-Z$). Zatem dla dowolnej trójki liczb, gdy rozważymy różnice pomiędzy nimi, któraś z różnic będzie sumą pozostałych dwóch.

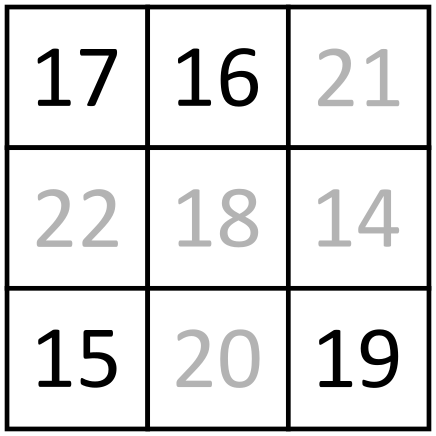
Możemy teraz wrócić do rozwiązania zagadki. Niech nieznana różnica będzie tą pomiędzy $C$ i $D$. Weżmy liczby $A$, $B$ i $C$. Wszystkie różnice pomiędzy nimi są znane. Ponieważ jedna z nich musi być sumą dwóch pozostałych istnieją jedynie dwie możliwości: $7+8=15$ lub $8+10=18$. Analogiczna zależność musi zachodzić dla trójki $A$, $B$ i $D$. Stąd jedna z tych trójek będzie miała różnice $7$, $8$ a $15$ druga będzie miała różnice $8$, $10$ i $18$. Niech trójka $A$, $B$ i $C$ będzie miała (w pewnej kolejności) różnice $7$, $8$ i $15$. Trójki $A$, $B$, $C$ i $A$, $B$, $D$ mają wspólną różnicę jedynie pomiędzy $A$ i $B$, stąd ta wspólna różnica musi wynosić $8$.

Bez straty ogólności liczby $A$ i $B$ mogą być zamienione, możemy założyć więc że róznica pomiędzy $A$ i $C$ wynosi $15$, a różnica pomiędzy $B$ i $C$ wynosi $7$. W trójce $A$, $B$ i $C$ wiemy, że jedna z liczb $A$ i $C$ jest największa, a jedna najmniejsza (różnica pomiędzy nimi jest największa). Niech $A$ będzie największa. Mamy teraz dwa możliwe przypadki, ile mogą wynosić różnice pomiędzy liczbą $D$, a liczbami $A$ i $B$.

Przypadek 1: Różnica pomiędzy $A$ i $D$ wynosi $18$. To znaczy, że w trójce $A$, $B$ i $D$ jedna z liczb $A$ i $D$ jest największa, a jedna najmniejsza. Wybraliśmy jednak, że w trójce $A$, $B$ i $C$, liczba $A$ jest największa, więc $A$ jest większa od $B$. Stąd w trójce $A$, $B$, $D$ wiemy, że $A$ musi być największa. Mamy więc, że $A$ jest o $15$ większa niż $C$ i o $18$ większa niż $D$. Więc różnica pomiędzy $C$ i $D$ wynosi $(A-15)-(A-18)=3$. To wartość pierwszego rozwiązania.

Przypadek 2: Różnica pomiędzy $A$ i $D$ wynosi $10$. To znaczy, że w trójce $A$, $B$ i $D$ jedna z liczb $B$ i $D$ jest największa, a jedna najmniejsza. Analogicznie do poprzedniego przypadku wiemy, że $A$ jest większa od $B$, więc $B$ jest najmniejsza. Stąd wiemy, że $C$ jest o $7$ mniejsze od $B$ i, że $D$ jest o $18$ większe od $B$. To znaczy, że róznica pomiędzy $C$ i $D$ wynosi $(B+18)-(B-7)=25$. To wartość drugiego rozwiązania.

Podsumowując, nieznana różnica może wynosić $3$ lub $25$. To przekłada się na fakt, że w oryginalnym problemie, wartość nieznanego napięcia może wynosić jedynie $3V$ or $25V$. Stąd, suma dwóch możliwych wartości napięcia wynosi $3V+25V=28V$.

Wynik:

$91$

Zanim zaczniemy, zastanówmy się nad polem powierzchni trójkąta równobocznego o boku długości $x$. Używając twierdzenia Pitagorasa, łatwo policzyć, że wysokość takiego trójkąta to $\frac{\sqrt{3}}{2}x$. Zatem pole powierzchni trójkąta równobocznego wynosi $\frac{x\cdot \frac{\sqrt{3}}{2}x}{2}=\frac{\sqrt{3}}{4}{x}^2$.

Powróćmy do oryginalnego zadania. Oznaczmy wierzchołki sześciokąta przez $A$, $B$, $C$, $D$, $E$, $F$, tak by $\mathit{AB}=10m$, $\mathit{BC}=12m$, $\mathit{CD}=4m$, $\mathit{DE}=8m$, $\mathit{EF}=14m$, $\mathit{FA}=2m$. Przedłużmy te odcinki, tak by przecięły się otrzymując trójkąt $\mathit{KLM}$ taki jak na ilustracji:

Ponieważ wszystkie kąty wewnętrzne sześciokąta $\mathit{ABCDEF}$ mają miarę $120^{\circ }$, trójkąty $\mathit{KAF}$, $\mathit{LBC}$ oraz $\mathit{MDE}$ są równoboczne. To oznacza, że trójkąt $\mathit{KLM}$ jest równoboczny o boku długości $24m$.

Pole powierzchni sześciokąta $\mathit{ABCDEF}$ jest równe różnicy pola trójkąta równobocznego $\mathit{KLM}$ oraz sumy pól trójkątów $\mathit{KAF}$, $\mathit{LBC}$ oraz $\mathit{MDE}$. W takim razie możemy wyliczyć pole sześciokąta $\mathit{ABCDEF}$:

Zatem $a$ jest równe $91$.

Wynik:

$75$

Oznaczmy pole pierwszego tłoka przez $S_1$, pole drugiego tłoka – przez $S_2$ a pole trzeciego tłoka – przez $S_3$. Warunki zadania mówią nam, że $S_1=S_2+S_3$.

Niech $m$ oznacza masę chomika, a $\mathrm{\Delta }{h}_1=15\mathrm{mm}$ oznacza wysokość, o którą obniżył się pierwszy tłok po położeniu na nim chomika. Załóżmy, że w tym samym czasie tłok drugi podwyższył się o $\mathrm{\Delta }{h}_2$m a trzeci tłok – o $\mathrm{\Delta }{h}_3$. Gdy Miłosz położył chomika na pierwszym tłoku, musiały zadziać się dwie rzeczy. Po pierwsze, woda znajdująca się pod pierwszym tłokiem musiała zostać wypchnięta pod pozostałe dwa tłoki. To oznacza, że $S_1\mathrm{\Delta }{h}_1=S_2\mathrm{\Delta }{h}_2+S_3\mathrm{\Delta }{h}_3$. Po drugie, ciśnienie wywierane na wszystkie tłoki musiało być takie same. Jeśli $p$ oznacza początkowe ciśnienie wywierane na tłoki, a $\rho$ oznacza gęstość wody, możemy zapisać ten warunek jako: $p+\frac{\mathit{mg}}{S_1}-\mathrm{\Delta }{h}_1\mathit{\rho g}=p+\mathrm{\Delta }{h}_2\mathit{\rho g}=p+\mathrm{\Delta }{h}_3\mathit{\rho g}$ Możemy odjąć $p$ od wszystkich części tej równości i podzielić je przez $g$, żeby otrzymać $\frac{m}{S_1}-\mathrm{\Delta }{h}_1\rho =\mathrm{\Delta }{h}_2\rho =\mathrm{\Delta }{h}_3\rho$. Druga część tego równania mówi nam, że $\mathrm{\Delta }{h}_2=\mathrm{\Delta }{h}_3$. Po połączeniu tego faktu z poprzednimi równaniami otrzymujemy:

Innymi słowy:

Po porównaniu tych dwóch równań otrzymujemy:

Przedefiniujmy teraz $\mathrm{\Delta }{h}_2$ jako wysokość, o którą obniżył się drugi tłok po położeniu na nim chomika. W analogiczny sposób definiujemy na nowo $\mathrm{\Delta }{h}_3$. Metoda przedstawiona powyżej pozwala nam wyprowadzić trzy równania:

Jeśli podzielimy stronami dwa pierwsze równania i skorzystamy z tego, że $S_1=S_2+S_3$, otrzymamy:

Z $S_1=S_2+S_3$ wynika, że $S_3=S_1-S_2=S_1-\frac{2}{3}{S}_1=\frac{1}{3}{S}_1$. Dzieląc stronami drugie i trzecie równanie z tej samej listy równań otrzymujemy:

Zatem położenie chomika na trzecim tłoku obniży ten tłok o $75\mathrm{mm}$.

Wynik:

$999$

Ulubiona liczba Mateusza nie może być liczbą jednocyfrową. Jeśli byłały cyfrą $a$, własność z treści mówiłaby, że $a^2=a$, co jest prawdą tylko dla $a=0$ lub $a=1$. Wiemy jednak, że szukana liczba jest większa niż $1$.

Ulubiona liczba Mateusza nie może także być dwucyfrowa. Jeśli byłaby równa $10a+b$ dla pewnych cyfr $a$ oraz $b$, otrzymalibysmy ${(a+b)}^2=\mathit{ab}$, albo innymi słowy $a^2+\mathit{ab}+b^2=0$. Jednak skoro $b$ jest nieujemne oraz $a$ jest dodatnie, musi zachodzić $a^2+\mathit{ab}+b^2>0$, więc nie możemy otrzymać $a^2+\mathit{ab}+b^2=0$.

Teraz pokażemy, że $999$ jest jedyną trzycyfrową liczbą spełniającą warunek zadania. Łatwo sprawdzić, że faktycznie $999$ spełnia żądaną własność (${(9+9+9)}^2=27^2=3^6=9^3=9\cdot 9\cdot 9$).

Niech $100a+10b+c$ będzie liczbą o zadanej własności, co oznacza, że ${(a+b+c)}^2=\mathit{abc}$. $a$, $b$ i $c$ są cyframi, więc $0\le a,b,c\le 9$. Jeśli co najmniej jedna z liczb $a$, $b$ lub $c$ jest równa $0$, to łatwo zauważyć, że wszystkie pozostałe też muszą być równe $0$. Możemy więc założyć, że $1\le a,b,c$. Dodatkowo, zależność ${(a+b+c)}^2=\mathit{abc}$ jest symetryczna względem wartości $a$, $b$, $c$, więc możemy założyć, że $a\le b\le c$ (w taki sposób zawsze wyprodukujemy najmniejsze możliwe rozwiązanie dla dowolnej trójki cyfr spełniającej warunek). W takim razie:

Przyjrzyjmy się warunkowi ${(a+b+c)}^2=\mathit{abc}$. Możemy rozpisać go jako $a^2+b^2+c^2+2\mathit{ab}+2\mathit{ac}+2\mathit{bc}=\mathit{abc}$. Skoro $c\le 9$, wiemy że $\mathit{abc}\le 9\mathit{ab}$. Z drugiej strony, używając $a\le b\le c$, dostajemy:

Oraz ${(a-b)}^2\ge 0$, więc $a^2+b^2\ge 2\mathit{ab}$. Łącząc ze sobą te nierówności, dostajemy:

Ponieważ lewa i prawa strona tej nierówności są równe, we wszystkich użytych nierównościach, musi zachodzić równość.

• W nierówności $\mathit{abc}\le 9\mathit{ab}$ równość zachodzi wtedy i tylko wtedy, gdy $c=9$.
• W nierówności $\mathit{ac}\ge \mathit{ab}$ równość zachodzi wtedy i tylko wtedy, gdy $b=c$.
• W nierówności $\mathit{bc}\ge \mathit{ab}$ równość zachodzi wtedy i tylko wtedy, gdy $a=c$.

Te obserwacje prowadzą do konkluzji, że jedyny możliwy scenariusz to $a=b=c=9$. Sprawdziliśmy już, że istotnie jest to dozwolone rozwiązanie. W takim razie, $999$ jest jedyną trzycyfrową liczbą spełniającą warunek zadania. Zatem jest to najmniejsza liczba większa od $1$ z zadaną własnością, co oznacza, że ulubiona liczba Mateusza to $999$.

Wynik:

$250$

Rozumujemy podobnie jak w zadaniu 25. Niemniej tym razem musimy się zastanowić, jaki wpływ na układ mają różne współczynniki tarcia. Rozważmy najpierw ramiona, dla których współczynniki tarcia wynoszą $f_1=0,1$ oraz $f_3=0,3$. Największa możliwa siła tarcia statycznego dana jest przez wzór $\mathit{fF}$, czyli $F_f\le \mathit{fF}$. Mamy zatem dwie siły tarcia spełniające nierówności $F_{f_1}\le f_{1}F$ oraz $F_{f_3}\le f_{3}F$. Gdyby te dwie siły były różne, to powstałby moment siły działający wokół osi łączącej pozostałe dwa ramiona, co z kolei spowodowałoby niestabilność. Wobec tego musi być $F_{f_1}=F_{f_3}$, co w połączeniu z nierównością $f_1\le f_3$ daje $F_{f_1}=F_{f_3}=f_{1}F$. Podobnie dla $f_2=0,2$ oraz $f_4=0,4$ dostajemy równości $F_{f_2}=F_{f_4}=f_{2}F$. Siła grawitacji $F_g=\mathit{mg}$ musi zostać zrównoważona, skąd mamy równanie: