Výsledok:

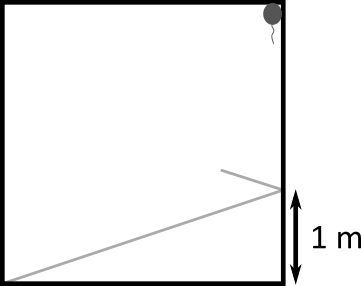
Keď skúsime niekoľkokrát odraziť lúč, tak to vyzerá, že lúč netrafí balón tak skoro. Navyše musíme zakaždým počítať, kde presne sa lúč odrazí, čo nie je až také jednoduché a príjemné. Skúsme teda niečo iné.
Skúsme namiesto preklápania lúča okolo kolmice na stenu, do ktorej lúč narazil, preklápať samotnú miestnosť. Povedzme, že vedľa pravej steny sa nachádza presne rovnaká miestnosť, akurát že preklopená podľa pravej steny pôvodnej miestnosti. Keby sme náš lúč nechali prejsť cez pravú stenu, tak by v tejto zrkadlovej miestnosti išiel presne rovnako, ako by išiel odrazený lúč v pôvodnej miestnosti. Opakovaním takéhoto preklápania môžeme predpokladať, že lúč sa pohybuje iba priamo a preklápame miestnosť.
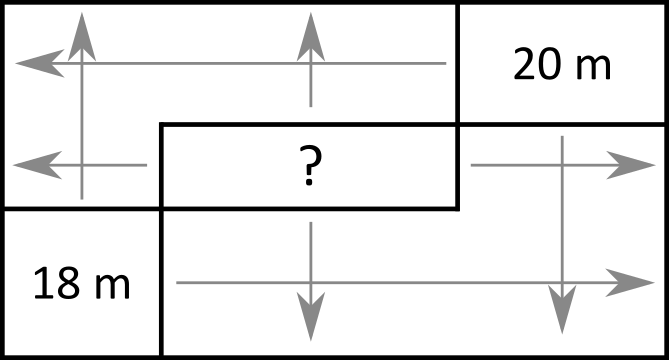
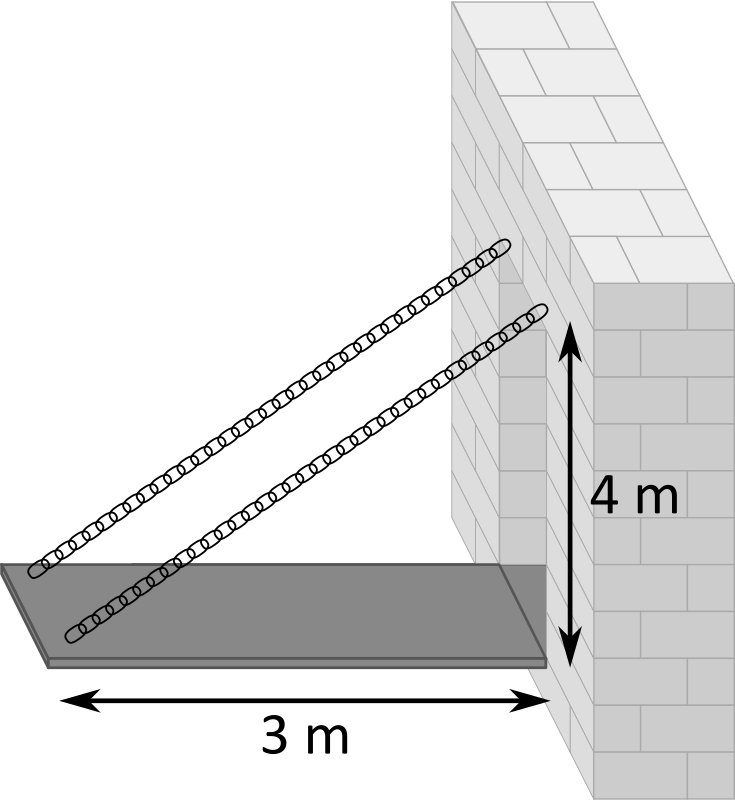
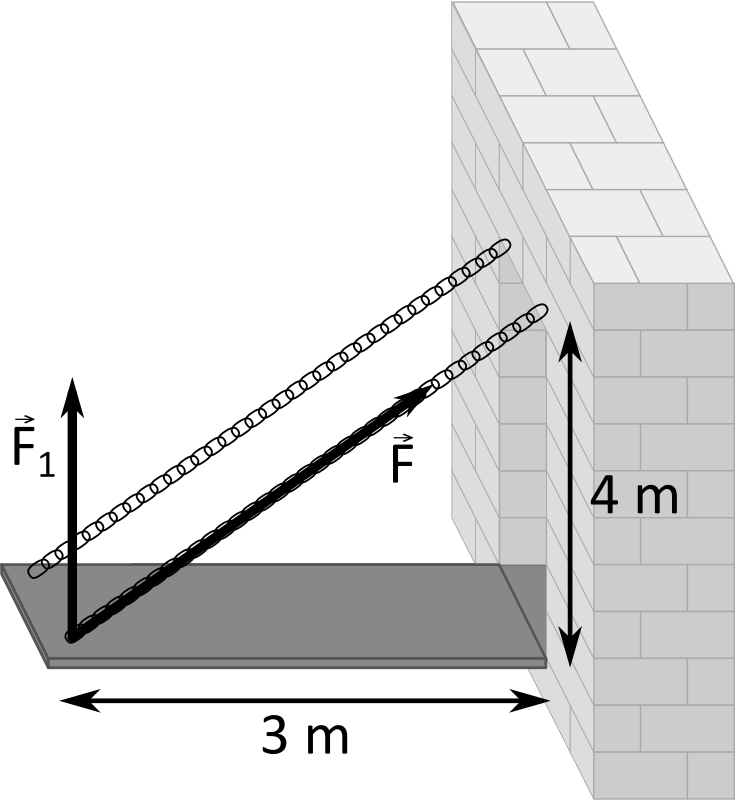
Z informácie o prvom odraze v pôvodnej situácii vieme, že vždy, keď sa priamy lúč posunie na obrázku doprava o  , tak sa posunie nahor o
, tak sa posunie nahor o  . Po istom čase sa lúč trafí presne do rohu niektorej preklopenej miestnosti a s trochou šťastia to bude ten, v ktorom sa nachádza aj balón. Lúč trafí nejaký roh, keď bude jeho prejdená vzdialenosť doprava aj prejdená vzdialenosť nahor nejakým násobkom dĺžky
. Po istom čase sa lúč trafí presne do rohu niektorej preklopenej miestnosti a s trochou šťastia to bude ten, v ktorom sa nachádza aj balón. Lúč trafí nejaký roh, keď bude jeho prejdená vzdialenosť doprava aj prejdená vzdialenosť nahor nejakým násobkom dĺžky  . Ak lúč prejde
. Ak lúč prejde  doprava, tak podľa prvej vety tohto odseku prejde
doprava, tak podľa prvej vety tohto odseku prejde  nahor. Keď je
nahor. Keď je  celé číslo, tak je
celé číslo, tak je  násobkom dĺžky
násobkom dĺžky  , hľadáme teda najmenšie celé číslo
, hľadáme teda najmenšie celé číslo  , pre ktoré je
, pre ktoré je  násobkom
násobkom  . Keďže
. Keďže  , tak najmenšie také
, tak najmenšie také  musí byť
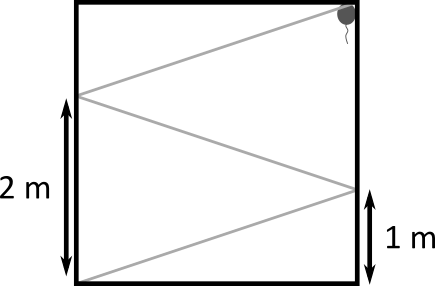
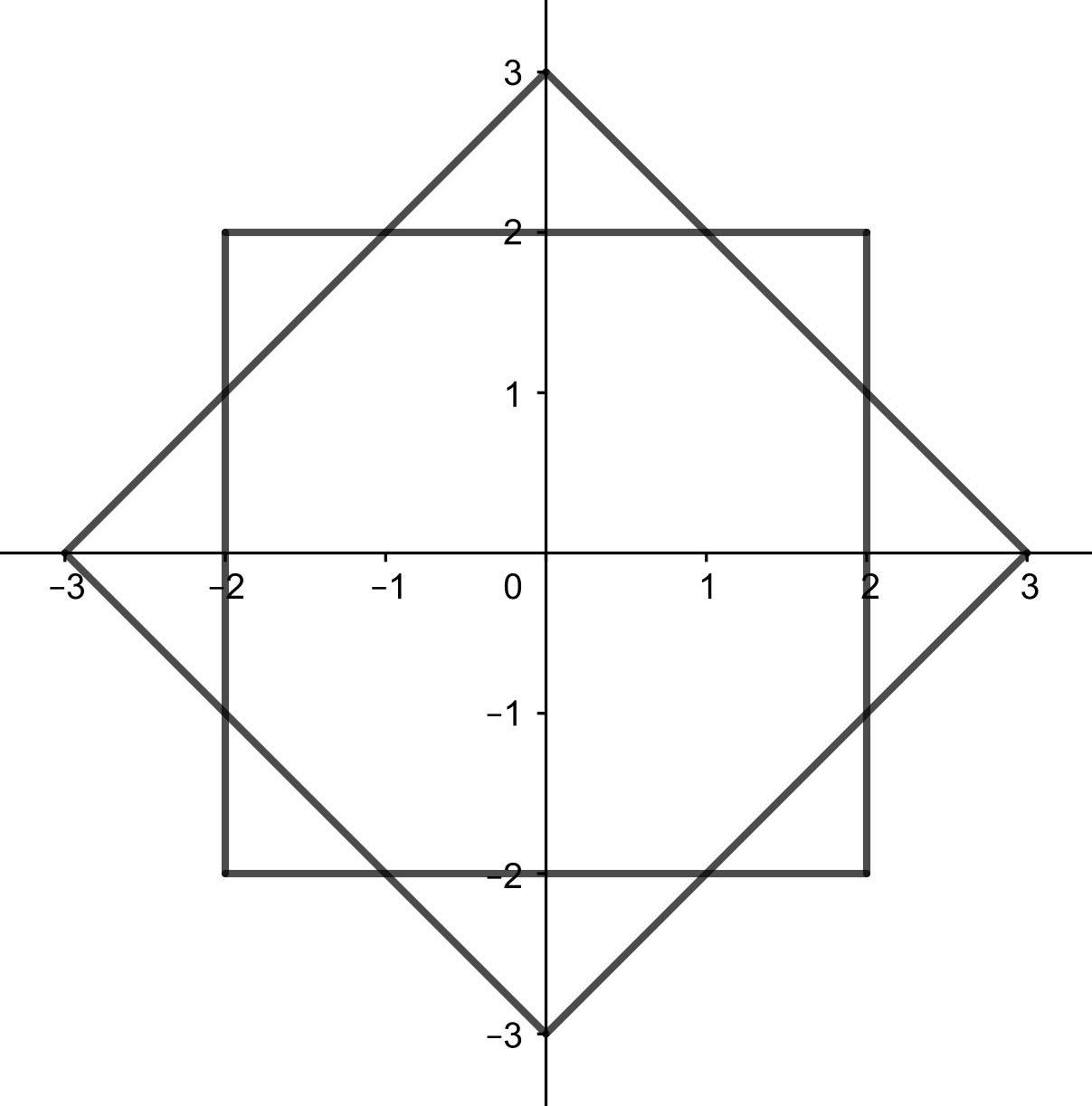
musí byť  . Situácia tak dopadla tak ako na obrázku:
. Situácia tak dopadla tak ako na obrázku:
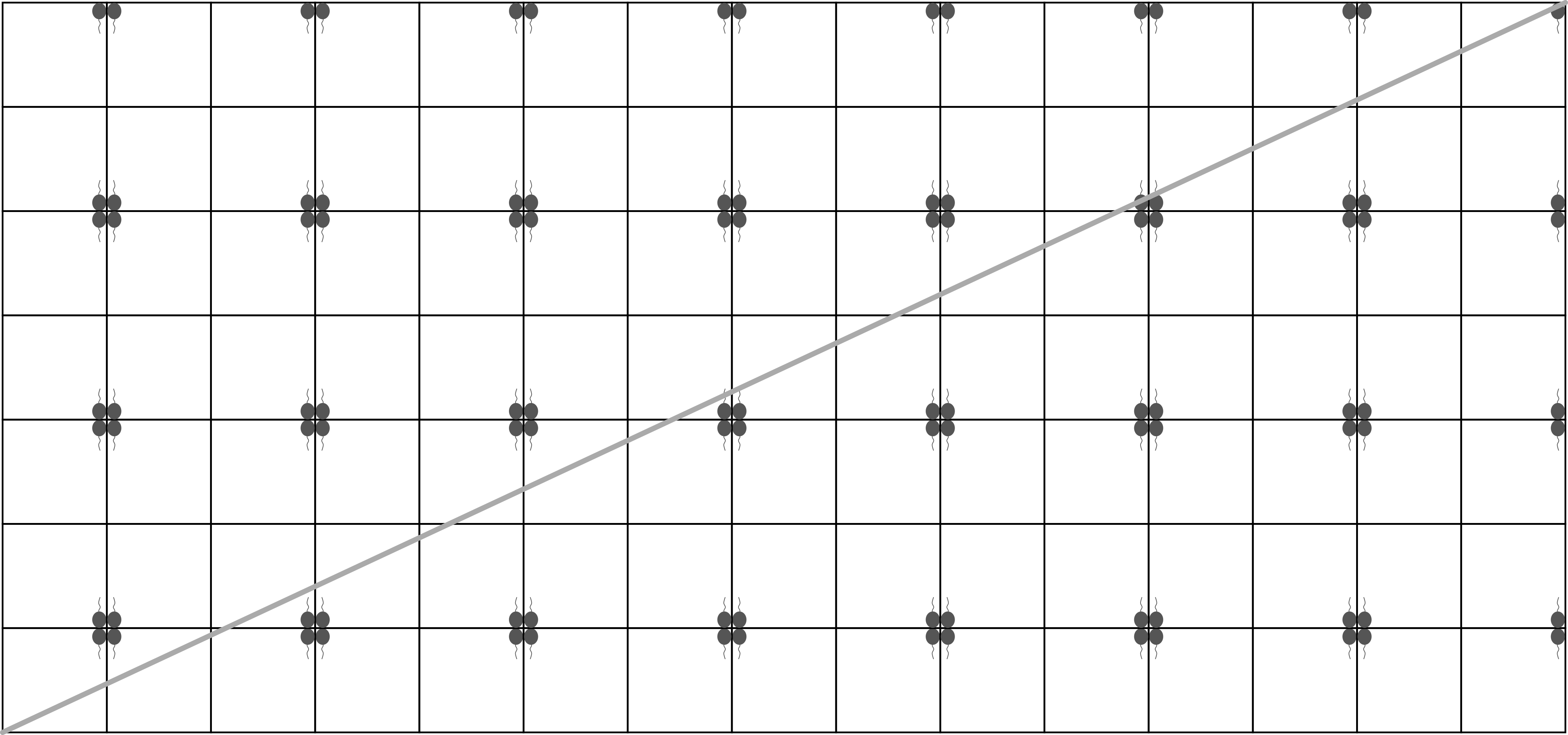
Z obrázka vidíme, že sme naozaj trafili správny roh (ten, v ktorom je balón). Ako ale spočítať počet odrazov od steny? Odraz v našom prerobení úlohy zodpovedá tomu, že lúč prešiel do inej miestnosti. Z obrázka vidno, že lúč  -krát prešiel do miestnosti vpravo a
-krát prešiel do miestnosti vpravo a  -krát do miestnosti hore. Spolu teda prešiel do inej miestnosti
-krát do miestnosti hore. Spolu teda prešiel do inej miestnosti  -krát, čiže v pôvodnej formulácii úlohy sa odrazil
-krát, čiže v pôvodnej formulácii úlohy sa odrazil  -krát.
-krát.
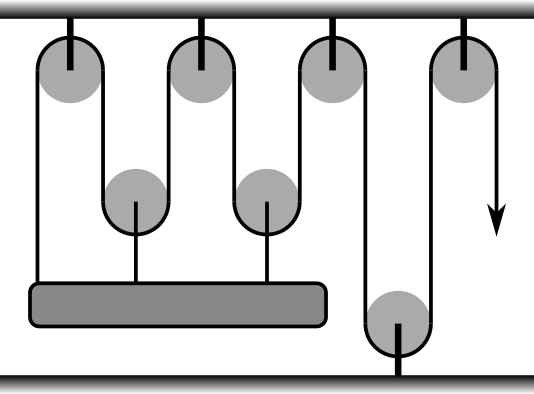
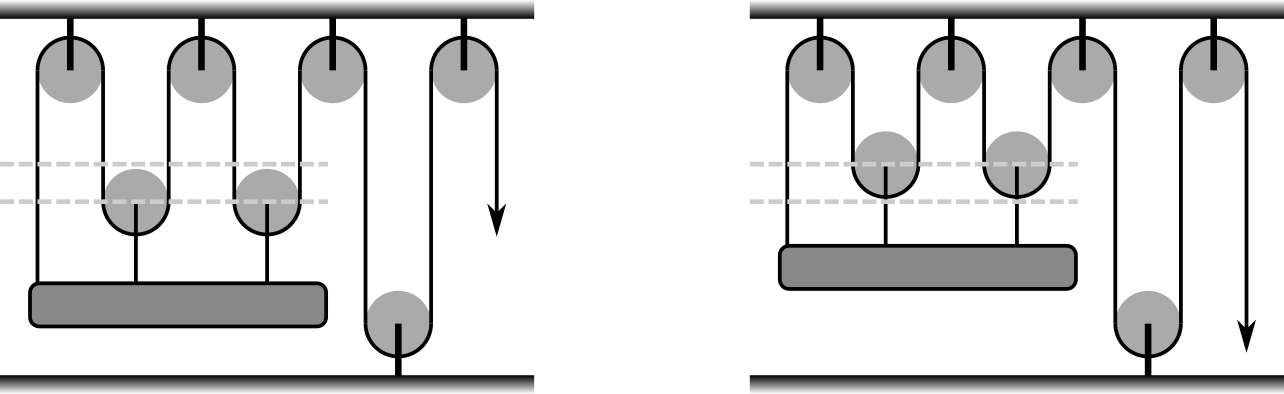
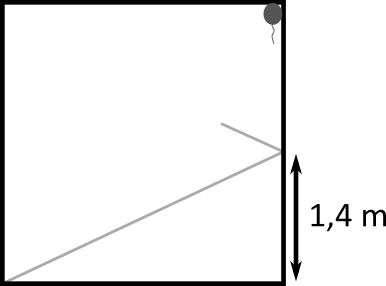
Poznámka: Na tomto obrázku možno vidno, ako presne sa lúč  -krát poodrážal, kým trafil balón:
-krát poodrážal, kým trafil balón:
. Každý rok jabloň narástla o
. Akú výšku v centimetroch má Žabova jabloň v rovnaký dátum v roku 2022?
. Počas každého z nasledujúcich desiatich rokov vyrástla jabloň o
. V roku 2022 má preto jabloň výšku
.