Zadania a riešenia úloh

Výsledok:

$27$

Keď Alica dala Borisovi jedenásť z jej kamienkov, prišla o $11$ kamienkov a Boris získal $11$ kamienkov. Takže rozdiel počtov kamienkov, ktoré majú, sa musel znížiť o $11+11=22$. Teda, Alica má o $49-22=27$ viac kamienkov ako Boris.

Výsledok:

$5$

Prvé tri mesiace roku $2023$ mali postupne $31$, $28$ a $31$ dní. Dokopy teda trvali $31+28+31=90$ dní, čo je $90\cdot 24=2160$ hodín. Tete teda prešla $10800$ kilometrov za $2160$ hodín. Jej priemerná rýchlosť preto bola $\frac{10800\mathrm{km}}{2160h}=5\mathrm{km}∕h$.

Výsledok:

$56$

Aby nakreslila spodné štyri štvorce, Laura musí nakresliť $13$ úsečiek. Aby pridala ďalšie tri štvorce nad nimi, potrebuje nakresliť ďalších $7$ úsečiek. Aby pridala dva štvorce v ďalšom poschodí, nakreslí ďalších $5$ úsečiek. Nakoniec, aby nakreslila vrchný štvorec, Laura potrebuje nakresliť $3$ úsečky. Dokopy teda nakreslí $13+7+5+3=28$ úsečiek. Každá z nich má dĺžku $2\mathrm{cm}$, teda celková dĺžka všetkých úsečiek je $28\cdot 2\mathrm{cm}=56\mathrm{cm}$.

Výsledok:

$45$

Dohľadaním si premien vo vzorcovníku zistíme, že $36\mathrm{oz}$ je $1l$. Teda objem plechovky koly v litroch je $\frac{12\mathrm{oz}}{36\mathrm{oz}∕l}=\frac{1}{3}l$. To znamená, že v jednom litri koly je $3\cdot 150=450$ kilokalórií, a teda v $100\mathrm{ml}$ koly je $450:10=45$ kilokalórií.

Výsledok:

$7$

Ak by v truhle bolo o $48$ mincí menej, každý pirát by dostal o $6$ mincí menej ako má teraz. Teda, dokopy musí byť $48:6=8$ pirátov. Keďže otázka znie, s koľkými členmi posádky si Anton delil mince, správna odpoveď je $8-1=7$.

Výsledok:

$4620$

Za $18$ minút prebehne Andrej $18:3=6$ koliečok. Každé z jeho koliečok má dĺžku $2\pi \cdot 70m=140\pi m$. Teda dokopy prejde vzdialenosť $6\cdot 140\pi m=840\pi m$. Keďže jeho krok má dĺžku práve jeden meter, urobí teda $840\pi$ krokov. Podobne, Žofka odbehne $18:2=9$ koliečok, z ktorých jedno má dĺžku $2\pi \cdot 35m=70\pi m$. Prejde teda $9\cdot 70\pi m=630\pi m$ čo znamená, že spraví $630\pi$ krokov. Spolu teda urobia $840\pi +630\pi =1470\pi$ krokov. Ak počítame s tým, že $\pi =\frac{22}{7}$ dostávame, že spravili $1470\cdot \frac{22}{7}=4620$ krokov.

Ak by sme použili $\pi =3,14$, dostali by sme výsledok $4615,8$, ktorý má po zaokrúhlení na desiatky rovnakú hodnotu ako pôvodný výsledok.

Výsledok:

$9$

Aby sme otvorili dvere minimálnou silou, musíme dosiahnuť rovnováhu momentov síl. Zatvárač dverí pôsobí momentom sily $M$ rovným sile od neho krát jeho vzdialenosti od pántov, teda $M=48N\cdot 15\mathrm{cm}=720N\mathrm{cm}$. Použitím tej istej rovnice dostaneme silu $F$ potrebnú na otvorenie dverí vo vzdialenosti $a=80\mathrm{cm}$ ako:

Výsledok:

$6,28$

Ak predpokladáme, že Zem je dokonalá guľa, lano omotané okolo jej rovníka vytýči kružnicu. Ak si označíme polomer tejto kružnice $r$, Evine lano bude merať $2\mathit{\pi r}$. Adam chce však vytýčiť kružnicu s polomerom $r+1m$. Preto Adamove lano musí merať $2\pi (r+1m)$. Rozdiel medzi dĺžkami Adamovho a Evinho lana teda bude $2\pi (r+1m)-2\mathit{\pi r}=2\pi m\doteq 6,28m$.

Výsledok:

$5$

Zakaždým, keď svetelný lúč narazí na zrkadlo, zmení svoj smer o $90^{\circ }$ buď doprava, alebo doľava (v závislosti od orientácie zrkadla). Ľahko nájdeme rozostavenie zrkadiel, kde nastane iba $5$ odrazov (je jedno, ako sú orientované zrkadlá v prázdnych políčkach):

Na druhej strane je vidno, že lúč nemohol ísť po najkratšej možnej ceste - idúcej cez $3$ políčka (vo viacerých políčkach by totiž nezmenil svoj smer). Navyše sa dá všimnúť, že počet odrazov musí byť nepárny - po každom nepárnom odraze ide lúč zvislo a po každom párnom odraze vodorovne.

Takže počet odrazov musí byť nepárne číslo väčšie ako $3$, čo znamená, že $5$ je skutočne najmenší možný počet odrazov.

Výsledok:

$45$

Ak použijeme iba cifru $1$, dostaneme v danom intervale $5$ drsných čísel, konkrétne $11$, $111$, $1111$, $11111$ a $111111$. Podobne dostaneme $5$ drsných čísel pre každú z cifier od $2$ do $9$, pričom nedostaneme žiadne drsné čísla pre cifru $0$. Teda existuje $9\cdot 5=45$ drsných čísel väčších ako desať a menších ako milión.

Výsledok:

$1$

Súčet všetkých čísel, ktoré píšeme na tabuľu je $0+1+2+3+4+5+6=21$. To znamená, že súčet čísel v každom zo stĺpcov bude $21:3=7$. To znamená, že číslo $0$ nemôže byť v prvom ani poslednom stĺpci, pretože by sme potrebovali použiť číslo $7$, ktoré však nemáme k dispozícií. Teda číslo $0$ bude použité v strednom stĺpci, čo spôsobí, že súčin čísel v strednom stĺpci bude vždy $0$. Preto môže Danko dostať iba $1$ možný súčin, konkrétne číslo $0$.

Výsledok:

$250$

Ak by Peter nebol zabudol zazátkovať odtok, vaňa by sa naplnila za $150l:0,2l∕s=750s$. Ale Peter zabudol zazátkovať odtok, čo znížilo prítok vody na $0,2l∕s-0,05l∕s=0,15l∕s$. Vaňa sa takto naplní za $150l:0,15l∕s=1000s$, teda jej napĺňanie bude trvať o $1000s-750s=250s$ dlhšie.

Výsledok:

$16$

Po prvom svojom pohybe, môže kráľ skončiť na ktoromkoľvek z týchto políčok:

Otázkou teraz je, na koľko rôznych políčok môže kráľ dojsť ďalším ťahom z ktoréhokoľvek z políčok ukázaných na predošlom obrázku. Ľahko nájdeme, že ďalším pohybom môže kráľ skončiť na ktoromkoľvek z týchto $16$ políčok:

Výsledok:

$14$

Dva nové trojuholníky majú niektoré strany rovnaké ako strany pôvodného štvoruholníka a tiež majú jednu stranu dlhú ako spomínaná uhlopriečka. To znamená, že nový súčet obvodov sa rovná pôvodnému obvodu zväčšenému o dvojnásobok dĺžky uhlopriečky. Keďže sa obvod zväčšil o $77\mathrm{cm}-49\mathrm{cm}=28\mathrm{cm}$, musí mať uvažovaná uhlopriečka dĺžku $28\mathrm{cm}:2=14\mathrm{cm}$.

Výsledok:

$10$

Vodorovná zložka rýchlosti loptičky po vyhodení bude $9\mathrm{km}∕h=2,5m∕s$. V tom momente Serena zrýchli na rýchlosť $18\mathrm{km}∕h=5m∕s$. Takže relatívna rýchlosť medzi Serenou a loptičkou bude $5m∕s-2,5m∕s=2,5m∕s$. Po $4$ sekundách, po ktorých loptička dopadne na zem, bude preto vzdialenosť medzi Serenou a loptičkou $2,5m∕s\cdot 4s=10m$.

Výsledok:

CDAB

Najprv určime, koľká v poradí prišla Alica. Keďže všetky tvrdenia sú nepravdivé, tak Alica nemohla prísť ako druhá. Barbora prišla po Alici a Cecília zas pred Alicou. To znamená, že aspoň jedno dievča prišlo pred a aspoň jedno dievča po tom, ako prišla Alica. Takže Alica nemohla prísť ani prvá a ani posledná. Zostáva teda iba možnosť, že Alica prišla ako tretia.

Barbora prišla po Alici, takže musela prísť posledná. Danica neprišla ako prvá, takže jej zostáva už len druhé miesto, keďže tretie a posledné miesto sú už obsadené. Napokon umiestnime Cecíliu na prvé miesto, na posledné zostávajúce miesto, a zjavne je jej tvrdenie skutočne nepravdivé.

Poradie, v ktorom prišli dievčatá, je teda Cecília, Danica, Alica a Barbora (CDAB).

Výsledok:

$5$

Poďme spočítať interval električky $12$. Keď ňou Kubko jazdí, jeho relatívna rýchlosť vzhľadom na oproti idúce električky je dvojnásobná oproti skutočnej rýchlosti električiek. Takže pozoruje, že električky prekonajú konštantnú vzdialenosť medzi po sebe idúcimi električkami dvakrát rýchlejšie. Preto je interval obsluhovania zastávky električkou $12$ dvakrát taký dlhý ako interval, v akom Kubko pozoruje električky v opačnom smere. Električka $12$ tak obsluhuje zastávku raz za každé $2\cdot 2=4$ minúty. Za hodinu teda obslúži zastávku $60:4=15$ električiek s číslom $12$.

Podobne, $60:6=10$ električiek s číslom $5$ obslúži zastávku za hodinu. Za hodinu tak obslúži zastávku o $15-10=5$ viac električiek s číslom $12$ ako električiek s číslom $5$.

Výsledok:

$250$

Potrebujeme si rozmyslieť, ako bude trenie pôsobiť na krabicu. Trecia sila pôsobí iba na objekty, ktoré na seba pôsobia nejakou tlakovou silou. Lenže v našom prípade krabica netlačí na zvislú stenu. Na krabicu preto nebude pôsobiť žiadna trecia sila. To znamená, že jediná sila (okrem tej od Boba), ktorá bude pôsobiť na krabicu, je tiažová sila $F_G=\mathit{mg}$, kde $m=25\mathrm{kg}$ je hmotnosť krabice. Bob musí za lano ťahať rovnako veľkou silou, čiže musí ťahať silou s veľkosťou $F=\mathit{mg}=25\mathrm{kg}\cdot 10N∕\mathrm{kg}=250N$.

Výsledok:

$50$

Kajine požiadavky sú, aby zobrala aspoň $2$ malinové džemy, $5$ čučoriedkových džemov, $1$ černicový, $1$ brusnicový a $1$ jahodový džem. Rozmyslime si, čo by sa malo stať, aby niektorá z týchto podmienok nebola splnená. Najhoršia vec, ktorá sa mohla stať, aby Kala nemala aspoň $2$ malinové džemy, je, že zobrala džemy všetkých ostatných príchutí a $1$ malinový. Spolu $1+15+7+15+9=47$ džemov. Ale ak by vzala aspoň $48$ džemov, tento problém by nenastal. Podobne by bol problém vziať $4$ čučoriedkové džemy a všetky džemy ostatných príchutí - spolu $10+4+7+15+9=45$ džemov. Takže Kaja potrebuje vziať aspoň $46$ džemov. Opakovaním rovnakej myšlienky pre černice, brusnice a jahody zistíme, že žiadny problém nenastane, ak Kaja vezme postupne aspoň $(10+15+0+15+9)+1=50$, $(10+15+7+0+9)+1=42$ alebo $(10+15+7+15+0)+1=48$ džemov. Skombinovaním všetkého zistíme, že podmienky budú splnené, ak bude počet vzatých džemov najväčšie z čísel $48$, $46$, $50$, $42$, $48$. Preto musí Kaja zobrať aspoň $50$ džemov.

Výsledok:

$64$

Označme $s$ dĺžku závodu a $t$ čas víťaza v cieli. Vieme, že priemerná rýchlosť víťaza bola $24\mathrm{km}∕h$, takže $\frac{s}{t}=24\mathrm{km}∕h$.

Dve tretiny dĺžky závodu boli tvorené klesavými úsekmi, čiže dĺžka klesavých úsekov je $\frac{2}{3}s$. Navyše, víťaz strávil $3$-krát viac času v stúpavých úsekoch, čiže v klesavých úsekoch strávil čas $\frac{1}{4}t$. Priemerná rýchlosť víťaza v klesavých úsekoch je potom:

Dosadením $\frac{s}{t}=24\mathrm{km}∕h$ zisťujeme, že priemerná rýchlosť víťaza v klesavých úsekoch je:

Výsledok:

$95$

Pozrime sa na posledný riadok a na druhý stĺpec. Majú mať rovnaký súčet čísel, ale zároveň majú jedno políčko spoločné. To znamená, že aj čísla, ktoré nemajú spoločné, musia mať rovnaký súčet. Preto musí byť súčet čísel $15$ a $19$ rovnaký ako súčet čísla $16$ a čísla v prostrednom políčku. Tento súčet je $15+19=34$, takže v prostrednom políčku musí byť číslo $34-16=18$.

Teraz už máme všetky čísla na jednej z diagonál. Preto musí byť súčet čísel v každom riadku, každom stĺpci a na oboch diagonálach rovný $17+18+19=54$. S touto vedomosťou je jednoduché doplniť celú tabuľku.

Napokon spočítame, že súčet čísel, ktoré neboli napísané v tabuľke, je $21+22+18+14+20=95$.

Výsledok:

$0,8$

Každý $1m$ drôtu vieme nahradiť rezistorom s odporom $R_0=0,1\mathrm{\Omega }$. Keď toto spravíme, dostaneme nasledujúci diagram:

Teraz vieme použiť klasické vzťahy pre výpočet odporu rezistorov zapojených sériovo, resp. paralelene. Tým vypočítame, že odpor medzi bodmi $A$ a $B$ je

Výsledok:

$5$

Voda s objemom $V=150\mathrm{hl}$ má hmotnosť $m=V{\rho }_{\mathit{voda}}$. Aby sme ju zohriali z teploty $t_1=29\circ C$ na teplotu $t_2=33\circ C$, musíme jej dodať teplo $Q=c_{\mathit{voda}}m(t_2-t_1)=c_{\mathit{voda}}V{\rho }_{\mathit{voda}}(t_2-t_1)$. Toto teplo musí zodpovedať práci vykonanej solárnymi panelmi. Tie majú na každý meter štvorcový výkon $P_0=1,4\mathrm{kW}∕m^2$, takže ak majú solárne panely povrch $S$, tak dosahujú výkon $P=P_{0}S$. Po čase $t=10h$ vykonajú prácu $W=\mathit{Pt}=P_0\mathit{St}$. Táto práca sa vykoná na vode, takže musí platiť:

Anička preto potrebuje $5m^2$ solárnych panelov.

Výsledok:

$40$

Poradia, v ktorých padli góly, označujme reťazcom pozostávajúcom z písmen F a M, kde F zodpovedá gólu fyzikov a M gólu matematikov. V tomto značení máme týchto $10$ možných poradí, v ktorých mohli padnúť góly v prvom polčase: MMFFF, MFMFF, MFFMF, MFFFM, FMMFF, FMFMF, FMFFM, FFMMF, FFMFM, FFFMM. Rovnakým spôsobom zistíme, že zostávajúce $4$ góly v druhom polčase, mohli padnúť v $4$ možných poradiach: FMMM, MFMM, MMFM, MMMF. Prvý a druhý polčas sú od seba nezávislé, takže ľubovoľné poradie gólov v prvom polčase môžeme skombinovať s ľubovoľným poradím gólov v druhom polčase. Preto je celkový počet poradí, v ktorých mohli padnúť góly, rovný $10\cdot 4=40$.

Výsledok:

$125$

Keď robot tlačí silou $F$ do každej zo stien, tak trecie sily na každej stene sú $F_t=\mathit{fF}$, kde $f=0,3$ je súčiniteľ šmykového trenia, a smerujú nahor. Na druhej strane, na robota pôsobí tiažová sila $F_G=\mathit{mg}$ pôsobiaca smerom nadol. Aby bol robot v pokoji, musí mať táto tiažová sila rovnakú veľkosť ako súčet všetkých štyroch trecích síl. Preto musí platiť:

Takže sila $F$ musí mať veľkosť:

Výsledok:

$3$

Každý pravidelný šesťuholník sa dá rozdeliť na $6$ rovnostranných trojuholníkov. To nám umožňuje nakresliť trojuholníkovú sieť cez obrázok:

Z toho okamžite vidíme, že dĺžka strán šesťuholníkov (ktorá je rovnaká ako dĺžka strán trojuholníkov) je $12\mathrm{cm}:4=3\mathrm{cm}$.

Výsledok:

$1100$

Loď sa celá ponorí vtedy, keď budú tiažová a vztlaková sila rovnaké. Najväčšia možná vztlaková sila, ktorá vie pôsobiť na loď s objemom $V$ je podľa Archimedovho zákona $F_{\mathit{vz}}=V{\rho }_{\mathit{voda}}g$. Tiažová sila pozostáva z dvoch zložiek - tiažovej sily pôsobiacej na samotnú loď a tiažovej sily pôsobiacej na vodu, ktorá už stihla natiecť do lode. Tiažová sila pôsobiaca na loď s hmotnosťou $m$ je $F_{G_1}=\mathit{mg}$. Voda tečie do lode objemovým prietokom $Q$, takže za čas $t$ bude v lodi voda s objemom $V^{\prime }=\mathit{Qt}$. Takže tiažová sila pôsobiaca na vodu bude $F_{G_2}=\mathit{Qt}{\rho }_{\mathit{voda}}g$. Podmienka na ponorenie celej lode je $F_{\mathit{vz}}=F_{G_1}+F_{G_2}$, z ktorej jednoducho vyjadríme čas $t$:

To znamená, že loď sa celá ponorí za čas $t=1100s$

Výsledok:

$1990$

Obe dievčatá sčítali čísla od roku, v ktorom sa narodili, do roku $2023$. Danka dostala väčší súčet, takže sčitovala aj nejaké čísla, ktoré Janka nie. Keďže každý sčítanec má hodnotu približne $2000$, tak počet sčítancov, ktoré sčitovala iba Danka, je $19945:2000\doteq 10$. Preto ak sa Danka narodila v roku $x$, tak čísla sčitované iba Dankou sú $x$, $x+1$, …, $x+9$. Ich súčet je $10x+45$. Takto dostaneme rovnicu $10x+45=19945$, z ktorej zistíme, že Danka sa narodila v roku $x=\frac{19945-45}{10}=1990$.

Výsledok:

$11$

Skúšajme možnosti podľa toho, aká je orientácia prvého a posledného zrkadla. Tým dostaneme jednotlivé riadky tohto obrázka (pre lepšiu prehľadnosť doň nekreslíme ani svetelné lúče a ani zrkadlá, ktorých orientácia nezmení trajektóriu lúča):

Vidíme teda, že lúč mohol hračkou prejsť $1+3+3+4=11$ rôznymi trajektóriami.

Výsledok:

$\frac{68}{3}$

Predpokladajme, že dĺžky strán obdĺžnika $\mathit{ABCD}$ sú $|\mathit{AB}|=9x$ a $|\mathit{BC}|=8x$ pre nejaké $x$.

Najprv spočítajme obvod štvoruholníka $\mathit{ABEF}$. Odvesny v pravouhlom trojuholníku $\mathit{ECF}$ majú dĺžky $4x$ a $3x$. Takže Pytagorova veta dáva, že $|\mathit{EF}|=\sqrt{{(4x)}^2+{(3x)}^2}=5x$. Podobne majú odvesny v pravouhlom trojuholníku dĺžky $6x$ a $8x$, takže $|\mathit{FA}|=\sqrt{{(6x)}^2+{(8x)}^2}=10x$. Preto má obvod štvoruholníka $\mathit{ABEF}$ veľkosť $9x+4x+5x+10x=28x$.

Teraz spočítame obsah štvoruholníka $\mathit{ABEF}$. Pravouhlé trojuholníky $\mathit{ECF}$ a $\mathit{FDA}$ majú obsahy $\frac{(4x)\cdot (3x)}{2}=6x^2$ a $\frac{(6x)\cdot (8x)}{2}=24x^2$. Obsah obdĺžnika $\mathit{ABCD}$ je $(9x)\cdot (8x)=72x^2$, takže obsah štvoruholníka $\mathit{ABEF}$ je $72x^2-6x^2-24x^2=42x^2$.

Vieme, že číselné hodnoty obvodu a obsahu štvoruholníka $\mathit{ABEF}$ sú rovnaké, čo znamená:

Zostáva už len spočítať obvod obdĺžnika $\mathit{ABCD}$, ktorý je $9x+8x+9x+8x=34x=34\cdot \frac{2}{3}\mathrm{cm}=\frac{68}{3}\mathrm{cm}$.

Výsledok:

$2$

Práca dážďovky bude zodpovedať najväčšej potenciálnej energii, ktorú dážďovka počas preliezania cez kocku dosiahne (pritom predpokladáme, že jej potenciálna energia je na začiatku nulová). Ľahko vidno, že maximum sa dosiahne presne v tom momente, keď bude dážďovka v polohe ako na obrázku v zadaní (lebo čím viac jej častí bude vyššie, tým väčšiu potenciálnu energiu bude mať).

Rozdeľme dážďovku na $3$ časti (neobávajte sa, dážďovka sa zvládne zregenerovať) - dve zvislé a jednu vodorovnú ako na obrázku v zadaní. Všetky majú dĺžku $10\mathrm{cm}$, čo je tretina dĺžky dážďovky. Keďže dážďovka je homogénna, všetky $3$ časti majú hmotnosť $m_0=3g:3=1g$. Vodorovná časť má ťažisko vo výške $h_2=10\mathrm{cm}$, takže potenciálna energia tejto časti je $E_2=m_{0}g{h}_2=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,1m=0,001J=1\mathrm{mJ}$. Zvislé časti majú ťažisko vo výške $h_1=h_3=5\mathrm{cm}$, takže ich potenciálna energia je $E_1=E_3=m_{0}g{h}_1=m_{0}g{h}_3=0,001\mathrm{kg}\cdot 10N∕\mathrm{kg}\cdot 0,05m=0,0005J=0,5\mathrm{mJ}$.

Najväčšia potenciálna energia dážďovky bude preto $E=E_1+E_2+E_3=0,5\mathrm{mJ}+1\mathrm{mJ}+0,5\mathrm{mJ}=2\mathrm{mJ}$, čo je tiež práca, ktorú musí dážďovka vykonať.

Výsledok:

$1050$

Rozdeľme si úlohu na ľahšie stráviteľné kusy. Najprv, koľko pokusov musí vyskúšať, aby sa dostala k ABA? Keďže máme v anglickej abecede $26$ písmen, bude to trvať $26$ zmien posledného písmena. Ako to bude s BAA? Po každých $26$ zmenách posledného písmena sa druhé písmeno zmení o jedno, preto aby sme sa dostali k BAA z AAA, potrebujeme $26\cdot 26=676$ pokusov. Ďalej, na to, aby sme sa dostali na BOA z BAA, potrebujeme $26\cdot 14=364$ pokusov, keďže O je $15$. písmeno abecedy a musíme vyskúšať všetkých $14$ písmen predtým. Napokon, J je $10$. písmeno, takže potrebujeme ďalších $10$ pokusov, aby sme sa dostali na BOJ z BOA. To dokopy dáva, že Terka musí vyskúšať $676+364+10=1050$ kombinácií.

Výsledok:

$125$

Celý mechanizmus bude v pokoji iba vtedy, keď bude výsledný moment sily pôsobiaci na každú páku nulový. Pozrime sa teda na momenty síl pôsobiace na páky. Na to potrebujeme pochopiť, čo robia lanká. V lankách bude nejaké napätie, a tak bude každé lanko pôsobiť na obe páky rovnako veľkou silou ako je veľkosť tohto napätia. Napríklad lanko spájajúce prostrednú a pravú páku bude pôsobiť rovnako veľkou silou na prostrednú páku (smerom doprava) ako na pravú páku (smerom doľava). Navyše si všimnime, že obe tieto sily pôsobia v rovnakej výške, a tak pôsobia v rovnakej vzdialenosti od osi otáčania pák. Preto každé lanko pôsobí na obe páky rovnako veľkým momentom sily.

Toto v podstate znamená, že môžeme zabudnúť na prostrednú páku. Totižto, sila pôsobiaca na pravú páku vyvoláva moment sily veľkosti $M$ na pravú páku. Tento moment sily musí byť vykompenzovaný momentom sily od lanka pripevneného k pravej páke. Keďže lanká prenášajú moment sily, veľkosť momentu sily, ktorým pravé lanko pôsobí na prostrednú páku, musí byť tiež $M$. Podobne aj moment sily pôsobiaci na ľavú páku bude mať veľkosť $M$.

Preto aby bol celý mechanizmus v pokoji, musia obe uvažované sily vyvolávať rovnako veľký moment sily. Toto vedie k vzťahu:

Paťo teda musí ťahať ľavú páku silou v veľkosťou $125N$.

Výsledok:

$2,15$

Označme si jednotlivé vrcholy a dĺžky tak ako na tomto obrázku:

Uvažujme pravouhlé trojuholníky $\mathit{ABP}$ a $\mathit{ACP}$. Napíšme pre ne Pytagorovu vetu, čím dostaneme:

Keď vyjadríme $h^2$ z oboch rovností a vyjadrenia porovnáme, získame

Teraz použime vzťah $a^2-b^2=(a-b)(a+b)$ na obe strany rovnosti a dostaneme

Lenže vieme, že $y+x=20\mathrm{cm}$. Preto má rozdiel dĺžok $y-x$, ktorý máme spočítať, veľkosť:

Výsledok:

$75$

Označme hmotnosť vozíka $m$, polomer vertikálnej slučky $r=30m$ a rýchlosť vozíka v najvyššom bode vertikálnej slučky $v$.

Z prvej časti zadania vieme, že v najvyššom bode vertikálnej slučky musí na vozík pôsobiť dostredivá sila $F_d=\frac{m{v}^2}{r}$. Sú len dve sily, ktoré môžu na vozík pôsobiť v tomto smere tak, aby mohli byť touto dostredivou silou - tiažová sila $F_G=\mathit{mg}$ a nejaká sila od samotnej vertikálnej slučky. My však chceme mať dostredivú silu čo najmenšiu (čím väčšia by bola, tým väčšiu rýchlosť by musel mať vozík, a teda by musel mať na začiatku väčšiu energiu). A keďže gravitačnej sily sa nezbavíme, v prípade s najmenšou výškou budeme mať $F_d=F_G$. Z tohto dostávame:

Teraz sa pozrime na energie. Na začiatku mal vozík iba potenciálnu energiu

. Na vrchu vertikálnej slučky má však aj potenciálnu, aj kinetickú energiu. Je vo výške

a má rýchlosť

, takže jeho celková energia je

. Energia sa musí zachovať, takže

. Keď to dáme dokopy so vzťahom pre

, získame:

Preto musí byť vozík spustený z výšky aspoň $h=\frac{5}{2}r=\frac{5}{2}\cdot 30m=75m$.

Výsledok:

$23$

Riešenie tejto úlohy sa prirodzene delí na dve časti. V prvej ukážeme, že sa mohlo odohrať $23$ zápasov. V druhej časti potom ukážeme, že ak by sa odohralo $24$ zápasov, tak by už existovala skupina popísaná v zadaní. To bude znamenať, že odpoveď je $23$.

Prvá časť: Očíslujme si hráčov číslami $1$, $2$, …, $24$. Nech sú zápasy hrané medzi hráčmi $1$ a $2$, $2$ a $3$, …, $23$ a $24$ a zvoľme si nejakú skupinu hráčov. V tejto skupine je určite nejaký hráč, ktorý má najmenšie číslo, označme toto číslo $P$. V rámci tejto skupiny mohol tento hráč hrať zápas jedine s $P+1$ (ak je vôbec v skupine), pretože hráč s číslom $P-1$ nemôže byť v skupine (bol by to hráč s menším číslom ako $P$). Takže hráč s číslom $P$ určite nehral s aspoň $2$ ľuďmi v tejto skupine. Toto platí pre ľubovoľnú skupinu, takže naozaj neexistuje žiadna skupina, ktorá by spĺňala podmienku zo zadania. Čiže $23$ zápasov sa mohlo odohrať.

Druhá časť: Máme dokázať, že ak sa odohralo $24$ zápasov, tak vždy nájdeme skupinu s vlastnosťou zo zadania. Keby existovala taká dvojica hráčov, ktorá medzi sebou hrala dva zápasy, tvorila by skupina s vlastnosťou zo zadania. Preto predpokladajme, že takáto dvojica neexistuje.

Teraz predpokladajme, že každý hráč odohral aspoň $2$ zápasy. Vyberajme hráčov do skupiny nasledovne: Začnime s nejakým hráčom, nazvime ho $P_0$. S niekým hral zápas, povedzme, že s $P_1$. Hráč $P_1$ hral s aspoň dvomi hráčmi, takže hral aj s nejakým $P_2$ rôznym od $P_0$. Podobne aj pre $P_2$ nájdeme hráča $P_3$, s ktorým hral a ktorý je rôzny od $P_1$. Takto pokračujme vo vyberaní hráčov. Časom sa dostaneme k nejakému hráčovi, ktorého sme už vybrali. V tomto bode budeme mať hráčov $P_k$, $P_{k+1}$, …, $P_n$ s vlastnosťou, že každý z hráčov $P_i$ hral s hráčmi $P_{i-1}$ a $P_{i+1}$ a že hráči $P_k$ a $P_n$ hrali spolu zápas. Inými slovami, budeme schopní postaviť ich na kružnicu tak, že každý hráč hral so svojimi susedmi. Takže táto skupina hráčov má požadovanú vlastnosť. Preto ak každý hral aspoň $2$ zápasy, tak sme hotoví.

Zostáva skontrolovať, že sa stane, ak niekto hral menej ako $2$ zápasy. V tomto prípadne zabudnime na takéhoto hráča a na všetky zápasy, ktoré hral. Po tomto nám zostane menej hráčov, ale stále bude platiť, že sa hralo aspoň toľko zápasov, koľko zostáva hráčov. Po zabudnutí na tohto hráča máme dve možnosti. Buď už všetci zostávajúci hrali aspoň $2$ zápasy, alebo je opäť medzi hráčmi niekto, kto hral menej ako $2$ zápasy. V prvom prípade ukazuje argument z predošlého odseku, že existuje skupina, ktorá spĺňa podmienky zo zadania. V druhom prípade máme ďalšieho hráča, na ktorého môžeme zabudnúť. Takýmto spôsobom pokračujeme. Ak budeme stále mať na koho zabudnúť, tak budeme znižovať počet hráčov, až napokon dostaneme skupinu $3$ hráčov, ktorý medzi sebou hrali aspoň $3$ zápasy. To je možné iba tak, že hrali každý s každým, takže tvoria skupinu, ktorú hľadáme.

Tým sme zdôvodnili, že ak by sa odohralo $24$ zápasov, tak by existovala skupina zo zadania.

Keď všetko dáme dokopy, tak sme dokázali, že sa mohlo odohrať najviac $23$ zápasov.

Výsledok:

$25$

Na začiatok musíme objaviť pravidlo o deliteľnosti $125$. Kritérium je, že posledné trojčíslie musí byť deliteľné $125$ (toto je podobné kritériám o deliteľnosti $2$, $4$, $8$, $16$ …, len s $5$, $25$, $125$ …). Prečo je to tak? Napíšme si nejaké číslo ako $1000A+B$, kde $B<1000$. Teda číslo $B$ je posledné trojčíslie pôvodného čísla. Všimnime si, že číslo $1000$ je deliteľné $125$, pretože $1000=8\cdot 125$. Takže na to, aby bolo číslo $1000A+B$ deliteľné $125$, musí byť $B$ deliteľné $125$. Týmto je platnosť kritéria dokázaná.

Teraz sa pozrime, aké má toto dôsledky. Jediné najviac trojciferné čísla deliteľné $125$ sú $0$, $125$, $250$, $375$, $500$, $625$, $750$ a $875$. Žiadne z nich sa nezačína cifrou $4$. Preto dostávame, že žiadny násobok $125$ nemôže mať na mieste stoviek cifru $4$.

Napokon sa vráťme k pôvodnej úlohe. Vieme, že Lucy dostala súčin, ktorý má na mieste stoviek cifru $4$, takže tento súčin nemôže byť násobok $125$. Keby Lucy nevynechala žiadne číslo, bol by jej súčin deliteľný $5\cdot 15\cdot 25$. Jeho prvočíselný rozklad by tak obsahoval štyrikrát prvočíslo $5$. Preto potrebujeme z prvočíselného rozkladu vyhodiť prvočíslo $5$ aspoň dvakrát. To sa dá iba tým, že Lucy vynechá číslo $25$. To znamená, že Lucy vynechala číslo $25$.

Výsledok:

$28$

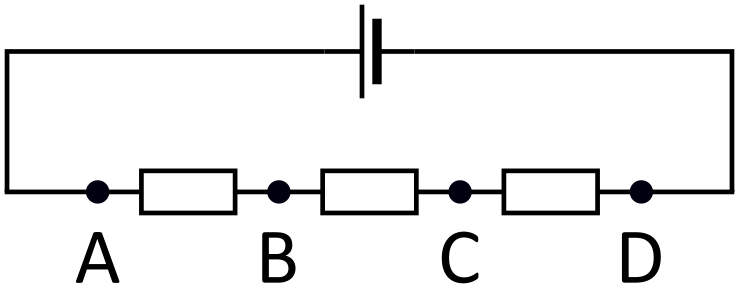
Napätie medzi dvomi bodmi popisuje veľkosť rozdielu potenciálov v týchto dvoch bodoch. Potenciál v bode popisuje iba (elektrickú) potenciálnu energiu častice s nábojom $1C$ v tomto bode. V každom z bodov $A$, $B$, $C$ a $D$ bude mať takáto častica nejakú potenciálnu energiu. Túto hodnotu potenciálnej energie môžeme priradiť každému z bodov. Potom napätia popisujú iba rozdiely medzi týmito hodnotami.

Preto môžeme našu úlohu preformulovať na čisto matematickú úlohu, v ktorej máme priradiť nejaké štyri čísla bodom $A$, $B$, $C$ a $D$ (teraz už tieto písmená nemajú nič spoločné s bodmi v pôvodnej fyzikálnej úlohe) tak, aby rozdiely medzi nimi boli $7$, $8$, $10$, $15$, $18$ a jeden neznámy rozdiel. Všimnime si zaujímavú vlastnosť. Vezmime tri z týchto čísel, napríklad $X$, $Y$ a $Z$, a povedzme si, že sú zoradené tak, že $X>Y>Z$. Potom je rozdiel $X-Z$ súčtom rozdielov $X-Y$ a $Y-Z$ (zjavne $(X-Y)+(Y-Z)=X-Z$). Preto ak si vezmeme ľubovoľnú trojicu z našich čísel, tak rozdiely medzi nimi budú mať tú vlastnosť, že jeden z nich je súčtom zvyšných dvoch.

Vráťme sa späť k našej úlohe. Povedzme si napríklad, že nepoznáme rozdiel medzi $C$ a $D$. Zoberme si čísla $A$, $B$ a $C$. Všetky tri rozdiely medzi nimi patria medzi tie známy. Lenže jeden z nich musí byť súčtom zvyšných dvoch, na čo máme len dve možnosti: $7+8=15$ or $8+10=18$. Rovnako to musí platiť aj pre trojicu $A$, $B$ a $D$, takže jedna z týchto trojíc bude mať rozdiely $7$, $8$ a $15$ a tá druhá bude mať rozdiely $8$, $10$ a $18$. Napríklad nech trojica $A$, $B$ a $C$ má (v nejakom poradí) rozdiely $7$, $8$ a $15$. Trojice $A$, $B$, $C$ a $A$, $B$, $D$ majú spoločný rozdiel medzi $A$ a $B$, takže tento rozdiel musí byť $8$ (je to totiž jediný spoločný rozdiel v trojiciach $7$, $8$, $15$ a $8$, $10$, $18$).

Doteraz boli role čísel $A$ a $B$ zameniteľné, takže si môžeme zvoliť napríklad, že rozdiel medzi $A$ a $C$ bude $15$ a že rozdiel medzi $B$ a $C$ bude $7$. V trojici $A$, $B$ a $C$ vieme, že z čísel $A$ a $C$ je jedno to najväčšie a jedno to najmenšie. Povedzme si, že $A$ bude to najväčšie. Na doriešenie nám zostáva už len pozrieť sa na to, aký je rozdiel medzi $D$ a číslami $A$ a $B$. Máme na to dve možnosti:

Prípad 1: Ak je rozdiel medzi $A$ a $D$ rovný $18$. Toto znamená, že v trojici $A$, $B$ a $D$ je jedno z čísel $A$ a $D$ to najväčšie a to druhé to najmenšie. Avšak v trojici $A$, $B$ a $C$ sme si to zvolili tak, že $A$ je najväčšie, čiže je väčšie ako $B$. Preto musí byť $A$ to najväčšie aj v trojici $A$, $B$, $D$. Toto dáva, že $A$ je $15$ väčšie ako $C$ a o $18$ väčšie ako $D$. Rozdiel medzi $C$ a $D$ je teda $(A-15)-(A-18)=3$. Toto je prvé riešenie.

Prípad 2: Ak je rozdiel medzi $A$ a $D$ rovný $10$. Toto znamená, že v trojici $A$, $B$ a $D$ je jedno z čísel $B$ a $D$ to najväčšie a to druhé to najmenšie. Podobne ako v predošlom prípade vieme, že $A$ je väčšie ako $B$, takže $B$ musí byť to najmenšie. Preto vieme, že $C$ je o $7$ menšie ako $B$ a že $D$ je o $18$ väčšie než $B$. To znamená, že rozdiel medzi $C$ a $D$ je $(B+18)-(B-7)=25$, čo dáva druhé riešenie.

Aby sme to zhrnuli, zistili sme, že hľadaný rozdiel môže byť buď $3$, alebo $25$. V pôvodnej úlohe to znamená, že neznáme napätie môže byť buď $3V$ alebo $25V$. Súčet dvoch možných hodnôt neznámeho napätia je preto $3V+25V=28V$.

Výsledok:

$91$

Skôr ako začneme, spočítajme obsah rovnostranného trojuholníka so stranou dĺžky $x$. Pomocou Pytagorovej vety jednoducho spočítame, že výška tohto trojuholníka je $\frac{\sqrt{3}}{2}x$. Takže obsah rovnostranného trojuholníka je $\frac{x\cdot \frac{\sqrt{3}}{2}x}{2}=\frac{\sqrt{3}}{4}{x}^2$.

Vráťme sa teraz k pôvodnej úlohe. Pomenujme jednotlivé vrcholy šesťuholníka $A$, $B$, $C$, $D$, $E$, $F$ tak, aby $|\mathit{AB}|=10m$, $|\mathit{BC}|=12m$, $|\mathit{CD}|=4m$, $|\mathit{DE}|=8m$, $|\mathit{EF}|=14m$, $|\mathit{FA}|=2m$. Pretnime priamky $\mathit{AB}$, $\mathit{CD}$ a $\mathit{EF}$. Tým dostaneme trojuholník $\mathit{KLM}$ ako na obrázku:

Z toho, že veľkosti vnútorných uhlov šesťuholníka $\mathit{ABCDEF}$ boli $120^{\circ }$, dostávame, že trojuholníky $\mathit{KAF}$, $\mathit{LBC}$ a $\mathit{MDE}$ sú rovnostranné. To rovno dáva, že aj trojuholník $\mathit{KLM}$ je rovnostranný, pričom dĺžka jeho strany je $24m$.

Obsah šesťuholníka $\mathit{ABCDEF}$ získame tak, že od obsahu trojuholníka $\mathit{KLM}$ odčítame obsahy trojuholníkov $\mathit{KAB}$, $\mathit{LBC}$ a $\mathit{MDE}$. Preto je obsah šesťuholníka $\mathit{ABCDEF}$ rovný:

To znamená, že hodnota $a$ je $91$.

Výsledok:

$75$

Označme si obsah prvého piestu $S_1$, druhého piestu $S_2$ a tretieho piestu $S_3$. Zadané podmienky nám vravia, že $S_1=S_2+S_3$.

Ďalej, nech $m$ je hmotnosť škrečka a $\mathrm{\Delta }{h}_1=15\mathrm{mm}$ je výška, o ktorú sa pohne prvý piest smerom nadol, keď naň Majo položí škrečka. V rovnakom momente sa druhý piest pohne nahor o $\mathrm{\Delta }{h}_2$ a tretí piest o $\mathrm{\Delta }{h}_3$. Po položení škrečka na prvý piest sa musia stať dve veci. Prvá z nich je, že voda spod prvého piestu sa musí rozdeliť pod zvyšné piesty. Toto dáva podmienku $S_1\mathrm{\Delta }{h}_1=S_2\mathrm{\Delta }{h}_2+S_3\mathrm{\Delta }{h}_3$. Na druhej strane, tlak pod všetkými tromi piestami musí byť rovnaký. Ak bol $p$ pôvodný tlak v systéme a $\rho$ je hustota vody, tak z tohto dostávame $p+\frac{\mathit{mg}}{S_1}-\mathrm{\Delta }{h}_1\mathit{\rho g}=p+\mathrm{\Delta }{h}_2\mathit{\rho g}=p+\mathrm{\Delta }{h}_3\mathit{\rho g}$. Po odčítaní $p$ a po predelení $g$ máme $\frac{m}{S_1}-\mathrm{\Delta }{h}_1\rho =\mathrm{\Delta }{h}_2\rho =\mathrm{\Delta }{h}_3\rho$. Druhá časť tejto rovnosti dáva $\mathrm{\Delta }{h}_2=\mathrm{\Delta }{h}_3$. Keď todo použijeme v predošlých vzťahoch, dostaneme:

Alebo po úprave:

Porovnaním týchto dvoch rovností dostávame:

Preznačme si $\mathrm{\Delta }{h}_2$, aby označovalo výšku, o ktorú sa druhý piest pohne nadol, keď naň Majo položí škrečka. Podobne označme túto veličinu $\mathrm{\Delta }{h}_3$ pre tretí piest. Rovnakým spôsobom, ako vyššie, získame:

Predelením prvých dvoch rovníc a použitím $S_1=S_2+S_3$, dostávame:

Z $S_1=S_2+S_3$ máme, že $S_3=S_1-S_2=S_1-\frac{2}{3}{S}_1=\frac{1}{3}{S}_1$. Keď v predošlej sade rovníc predelíme prvú a tretiu, dostaneme:

Takže ak položíme škrečka na tretí piest, tak ten sa pohne nadol o $75\mathrm{mm}$.

Výsledok:

$999$

Maťkove obľúbené číslo nemôže byť jednociferné. Ak by to bola cifra $a$, podmienka by hovorila, že $a^2=a$, čo platí len pre $a=0$ alebo $a=1$, no hľadané číslo by malo byť väčšie než $1$.

Maťkove obľúbené číslo tiež nemôže byť dvojciferné. Vskutku, ak by toto číslo bolo zapísané v tvare $10a+b$, dostali by sme ${(a+b)}^2=\mathit{ab}$, čiže $a^2+\mathit{ab}+b^2=0$. Ale keďže $a$ a $b$ nie sú záporné a $a$ je kladné, vždy dostaneme $a^2+\mathit{ab}+b^2>0$, čiže $a^2+\mathit{ab}+b^2=0$ nemôže nikdy platiť.

Ďalej ukážeme, že $999$ je jediné trojciferné číslo s danými vlastnosťami. Je jednoduché skontrolovať, že $999$ dané vlastnosti má (${(9+9+9)}^2=27^2=3^6=9^3=9\cdot 9\cdot 9$).

Nech $100a+10b+c$ je trojciferné číslo spĺňajúce potrebné podmienky, teda platí ${(a+b+c)}^2=\mathit{abc}$. Čísla $a$, $b$ a $c$ sú cifry, takže musí platiť, že $0\le a,b,c\le 9$. Zjavne, ak je niektorá z cifier $0$, vzťah ${(a+b+c)}^2=\mathit{abc}$ núti všetky ostatné cifry byť tiež $0$. Preto môžeme predpokladať, že $1\le a,b,c$. Navyše, vzťah ${(a+b+c)}^2=\mathit{abc}$ je pre hodnoty $a$, $b$, $c$ symetrický, čiže môžeme predpokladať, že $a\le b\le c$ (táto podmienka vytvorí z ktoréhokoľvek platného trojčíslia to najmenšie trojciferné číslo). Teda predpokladáme, že:

Pozrime sa bližšie na vzťah ${(a+b+c)}^2=\mathit{abc}$. Môže ho prepísať aj ako $a^2+b^2+c^2+2\mathit{ab}+2\mathit{ac}+2\mathit{bc}=\mathit{abc}$. Použitím $c\le 9$ vieme, že $\mathit{abc}\le 9\mathit{ab}$. Na druhú stranu, použitím $a\le b\le c$ vieme, že:

Taktiež, ${(a-b)}^2\ge 0$, čiže $a^2+b^2\ge 2\mathit{ab}$. Spojením týchto nerovností dostávame, že:

Keďže ľavá a pravá strana tejto nerovnosti je rovnaká, musíme mať rovnosti vo všetkých použitých nerovnostiach.

• V nerovnosti $\mathit{abc}\le 9\mathit{ab}$ nastáva rovnosť iba vtedy, keď $c=9$.
• V nerovnosti $\mathit{ac}\ge \mathit{ab}$ nastáva rovnosť iba vtedy, keď $b=c$.
• V nerovnosti $\mathit{bc}\ge \mathit{ab}$ nastáva rovnosť iba vtedy, keď $a=c$.

Zlúčením všetkých týchto troch pozorovaní dostávame, že jediným možným prípadom je $a=b=c=9$. Ako sme už skontrolovali, toto naozaj je riešenie. Čiže číslo $999$ je jediným trojciferným číslom, ktoré spĺňa uvedené podmienky. Teda je najmenším číslom väčším ako $1$ s danými vlastnosťami, teda $999$ je Maťkovým obľúbeným číslom.